Are Your Reasoning Models Reasoning or Guessing? A Mechanistic Analysis of Hierarchical Reasoning Models
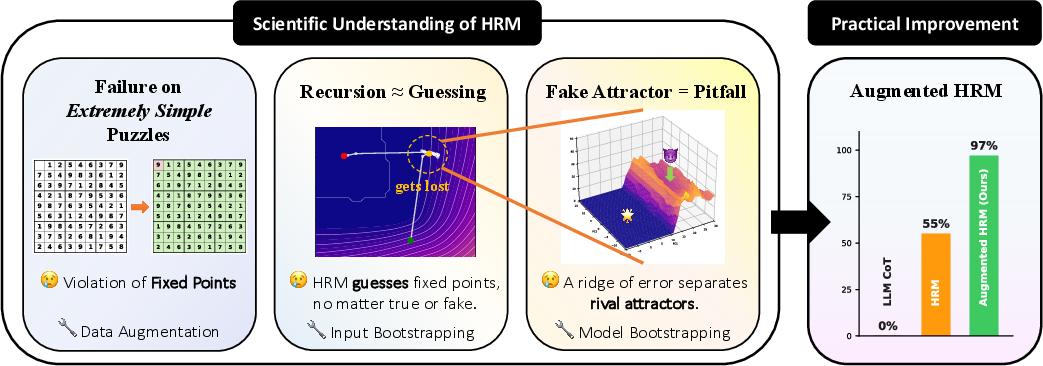
Abstract: Hierarchical reasoning model (HRM) achieves extraordinary performance on various reasoning tasks, significantly outperforming LLM-based reasoners. To understand the strengths and potential failure modes of HRM, we conduct a mechanistic study on its reasoning patterns and find three surprising facts: (a) Failure of extremely simple puzzles, e.g., HRM can fail on a puzzle with only one unknown cell. We attribute this failure to the violation of the fixed point property, a fundamental assumption of HRM. (b) "Grokking" dynamics in reasoning steps, i.e., the answer is not improved uniformly, but instead there is a critical reasoning step that suddenly makes the answer correct; (c) Existence of multiple fixed points. HRM "guesses" the first fixed point, which could be incorrect, and gets trapped there for a while or forever. All facts imply that HRM appears to be "guessing" instead of "reasoning". Leveraging this "guessing" picture, we propose three strategies to scale HRM's guesses: data augmentation (scaling the quality of guesses), input perturbation (scaling the number of guesses by leveraging inference randomness), and model bootstrapping (scaling the number of guesses by leveraging training randomness). On the practical side, by combining all methods, we develop Augmented HRM, boosting accuracy on Sudoku-Extreme from 54.5% to 96.9%. On the scientific side, our analysis provides new insights into how reasoning models "reason".
Summary
- The paper demonstrates that HRMs can transition from structured reasoning to systematic guessing, challenging the fixed-point assumption.
- The study reports a notable accuracy boost from 54.5% to 96.9% on Sudoku-Extreme through augmented training techniques.
- The research proposes bootstrapping, input perturbations, and diversified data as effective strategies to enhance latent state stability.
Mechanistic Insights into Reasoning versus Guessing in Hierarchical Reasoning Models
Introduction
This work presents a comprehensive mechanistic analysis of Hierarchical Reasoning Models (HRMs), emphasizing latent-space reasoning in complex structured environments such as Sudoku-Extreme. HRMs have shown robust performance on reasoning-intensive tasks but the paper rigorously interrogates the assumptions underlying their success. Notably, it differentiates "reasoning" from "guessing" within HRM dynamics by investigating latent trajectories, fixed-point properties, and scaling techniques.
Hierarchical Reasoning Model Architecture and Training
HRM operates by iteratively updating a latent state via segments within an outer recursive loop. The inputs, typically structured puzzles, are mapped into high-dimensional embeddings, and each segment applies a deterministic update to the latent state. Final predictions are decoded from the terminal latent state, potentially using adaptive halting mechanisms.
Training is centered around deep supervision, assigning supervision signal to every segment, and is enabled by the one-step gradient method. This approach detaches intermediate latent states, allowing computational scaling without quadratic cost in reasoning depth.
Fixed-Point Assumption and Empirical Violation
Central to the HRM's theoretical foundation is the fixed-point assumption: once the correct latent state (solution) is reached, further recursion should leave the solution invariant, justifying efficient training gradients.
Empirically, the paper demonstrates categorical violation of this assumption. HRMs can fail on extremely simple puzzles—such as those with only a single masked cell—despite theoretical guarantees, continually updating away from correct solutions in later segments.
Figure 1: Empirical demonstration of fixed-point violation and recovery via augmentation; accuracy increases from 54.5% to 96.9% through bootstrapped guessing and data augmentation.
These failures are attributed to insufficient exposure during training to easy or nearly-solved instances, a data distribution mismatch that postpones the model’s acquisition of stability near fixed points. Augmenting training with simplified puzzles spanning varying difficulty restores the fixed-point property.
Figure 2: Visualization of reasoning trajectories; instability and recurrent update away from correct answers on simple puzzles due to fixed-point violation.
Figure 3: Data mixing restores symmetry and stability in latent trajectories across samples with analogous formats.
Latent-Space "Guessing": Grokking Dynamics and Reasoning Modes
The loss dynamics along the reasoning trajectory show non-intuitive behavior. While average segment-wise loss monotonically decreases, individual samples exhibit "grokking" dynamics—extended plateaus followed by abrupt error collapse—contradicting the anticipated progressive refinement of answers.
Figure 4: Mean loss over all samples decreases smoothly as reasoning segments deepen, indicating global iterative improvement.
Figure 5: Per-sample loss along segments displays grokking: flat plateau then sudden drop, emphasizing non-uniform contribution of reasoning steps.
A four-mode taxonomy of reasoning patterns emerges: trivial and non-trivial successes (rapid convergence, abrupt late leap), trivial failure (wandering), and non-trivial failure (convergence to spurious fixed points).
Figure 6: PCA visualization of latent state trajectories; four distinctive reasoning modes are evident across samples.
Spurious Fixed Points and Rival Attractors
The latent space is populated by multiple fixed points, not all corresponding to correct solutions. The model can become trapped in spurious attractors, with escape requiring significant perturbation or favorable initialization.
Figure 7: Rival attractors in latent space create sharp separations; initialization determines convergence toward correct or misleading fixed point.
Spurious fixed points frequently align with shallow local minima in heuristic energy landscapes measuring constraint violations. Although HRMs do not explicitly optimize these metrics, their recurrence dynamics are implicitly shaped by them.
Scaling "Guessing": Augmented HRM
The insight that HRMs perform a form of "guessing" rather than deliberate reasoning motivates new scaling strategies. The authors introduce finite attempts via ensemble model bootstrapping, input perturbations (such as symmetry-based relabeling), and augmented training distributions. These techniques transform the reasoning process from uniform refinement into a search across diverse initializations and formats, drastically enhancing accuracy.
Exact accuracy on Sudoku-Extreme is driven from 54.5% in vanilla HRM to 96.9% with Augmented HRM. Notably, input perturbations and model checkpoint ensembles are effective, demonstrating lack of coverage and intrinsic diversity among solution trajectories.
Implications and Future Directions
This work compels a reconsideration of what "reasoning" entails in latent-space recursive models. The findings indicate that, absent strong inductive biases, these architectures operate via search and "guessing" within high-dimensional attractor landscapes. The presence of spurious fixed points and grokking dynamics suggests limits in interpretability and reliability when applied to problems with subtle decision boundaries.
Pragmatically, leveraging diversity through bootstrapping, input transformations, and data mixing forms a robust axis for scaling reasoning systems. Further research should target explicit optimization of energy landscapes, understanding the geometry of attractor basins, and integrating mechanisms for systematic exploration and escape from local minima.
Theoretically, future work should clarify the distinction between reasoning, search, and guessing in both recursive and non-recursive reasoning models. Mechanistic analyses, as performed here, are indispensable for mapping these dynamics and establishing more rigorous guarantees around solution convergence, stability, and compositional generalization.
Conclusion
The mechanistic analysis of HRMs presented in this paper (2601.10679) elucidates fundamental limitations and strengths of latent-space recursive reasoning. The revelation that effective reasoning often reduces to structured guessing guides future architecture and training practices. Augmentation of reasoning attempts—via data, input, and model scaling—provides potent practical improvements and encourages deeper inquiry into the geometry and optimization landscapes underlying model behavior. These insights are applicable beyond HRM, informing the development and analysis of a broad class of recursive latent-space reasoners.
Whiteboard
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper looks inside a powerful “reasoning” AI called the Hierarchical Reasoning Model (HRM) to ask a simple question: is it really reasoning step by step, or mostly making lucky guesses? The authors study how HRM solves very hard Sudoku puzzles and uncover surprising behaviors that make it look more like a smart guesser than a careful thinker. They then show simple ways to boost its performance by embracing and improving this “guessing” behavior.
Key questions the paper asks
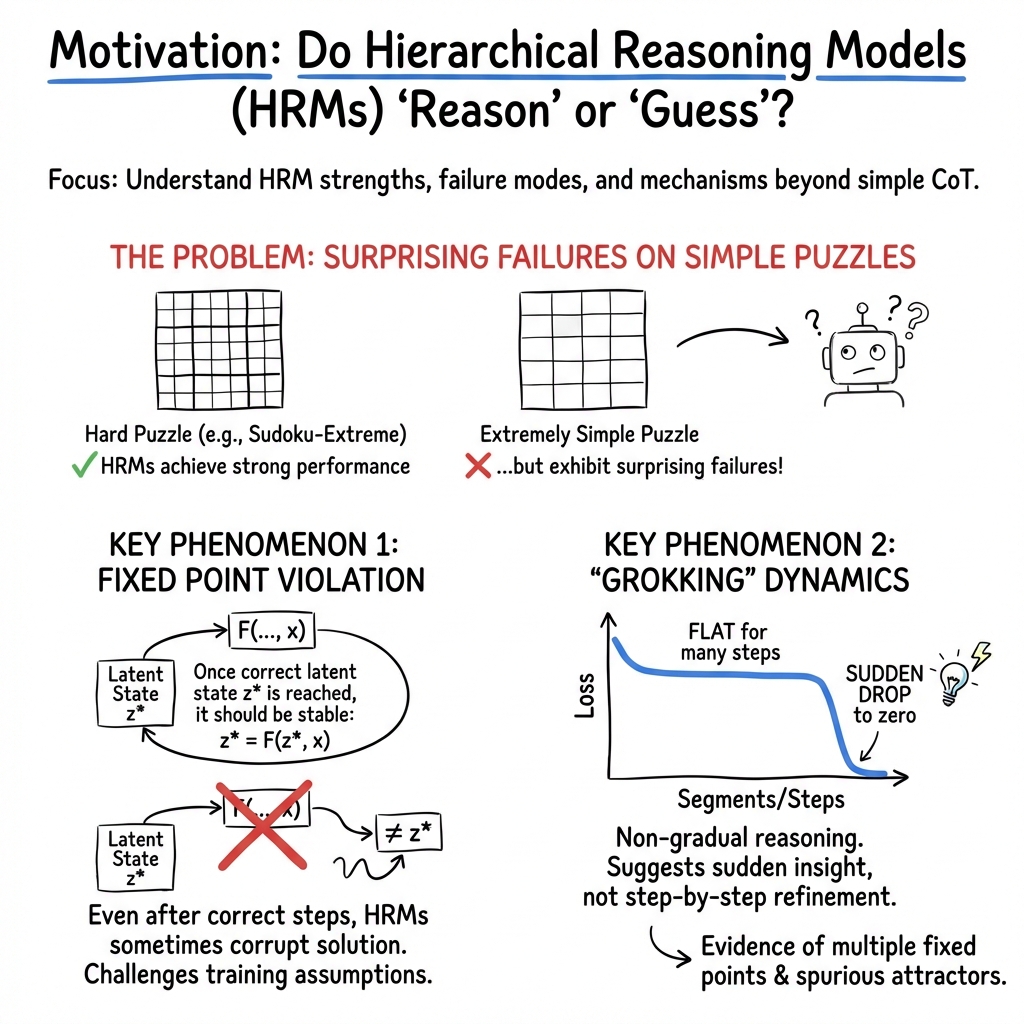
- Why does HRM sometimes fail on puzzles that are extremely easy for humans (like when only one Sudoku cell is blank)?
- When HRM uses many reasoning steps, does it improve gradually, or does it suddenly “get it” all at once?
- What hidden patterns (like “traps”) exist inside HRM’s internal thinking space that might cause it to get stuck?
- Can we improve HRM by giving it more or better “guess attempts”?
How they studied it (in simple terms)
Think of HRM like a person solving puzzles with a hidden scratchpad:
- It reads the puzzle, then runs through several internal “steps” (called segments) in a loop.
- After each step, it updates a hidden state—like notes on its scratchpad—before deciding on an answer.
- If it thinks it’s done, it can stop early (this is called adaptive stopping).
What the authors did:
- They tested HRM on very hard Sudokus (where HRM already does well) and on extremely simple ones (like only one empty cell).
- They “watched” the model’s internal scratchpad over time by projecting it onto a simpler 2D view (like turning a 3D maze into a top-down map) to see the path it takes while thinking.
- They tracked how the error changes after each step to see whether improvements were gradual or sudden.
- They tried adding small “nudges” (perturbations) in safe ways—by reshuffling the puzzle’s digits or using slightly different saved versions of the model—to see if that helps it escape bad paths.
A few technical ideas in everyday words:
- Latent space: the model’s hidden scratchpad where it keeps its thoughts.
- Fixed point: a stable state where, once the model has the right answer, it should stop changing its mind.
- “Grokking” dynamics: the error stays flat for many steps and then suddenly drops to zero—an “aha!” moment.
- Spurious fixed point: a tempting but wrong resting place—like a dead end that feels right.
Main findings and why they matter
- It can fail on extremely simple puzzles because it doesn’t hold onto correct answers
- What they found: HRM sometimes solves a simple Sudoku early, then keeps updating and breaks its own correct answer. Even worse, it can fail entirely on puzzles with just one missing cell.
- Why: The model’s training assumes a “fixed point” property—if it reaches the right state, it should stay there. In practice, this stability wasn’t learned well.
- Fix: Train with a mix of easy and hard versions of puzzles (data augmentation). This teaches the model to be stable near solutions and prevents it from “overthinking” after it’s correct. This raised accuracy from 54.5% to 59.9% and removed the weird failures on simple puzzles.
- HRM doesn’t improve bit by bit—it “groks” suddenly
- Average behavior looks smooth, but for each individual puzzle the error often stays stuck and then drops all at once. This suggests the model isn’t carefully refining the answer each step. Instead, it’s cycling through internal states until it lands on a good one—more like guessing than building a chain of small logical deductions.
- There are multiple resting places—some right, some wrong
- The model’s hidden space has several “attractors.” Some are true (lead to correct answers), others are spurious (feel stable but are wrong).
- If HRM starts closer to a wrong attractor, it can get trapped there for many steps—or forever.
- A simple “conflict counter” (counting Sudoku rule violations) helps explain this: wrong attractors can look like shallow “local minima” for this error, so the model isn’t naturally pushed out of them.
- Embracing the “guessing” view gives big improvements
- Since the model seems to be making structured guesses, the authors tried to scale the number and quality of those guesses:
- Better guesses: Train on both hard and easy puzzles (data mixing).
- More guesses via inputs: Transform the Sudoku by relabeling digits (e.g., swap all 1s and 9s), creating different but equivalent puzzles. The model treats each as a fresh attempt, then you map the answer back. This alone gave a big boost.
- More guesses via models: Use several nearby saved versions of the model (checkpoints) and let them “vote.”
- Combining these methods (called Augmented HRM) raised accuracy on the very hard Sudoku-Extreme benchmark from 54.5% to 96.9%.
Why this is important
- It challenges a common assumption: longer “thinking” doesn’t always mean better step-by-step reasoning. HRM’s success often comes from hitting the right internal state quickly, not from gradual logic.
- It shows that models can look like they’re reasoning when they’re actually navigating a hidden landscape with multiple attractors—some correct, some misleading.
- It offers practical, simple tools to make such models much stronger by:
- Training on a broader mix of difficulties (to learn stability),
- Trying multiple equivalent inputs (to escape traps),
- Using small ensembles of the model (to diversify guesses).
Takeaway and potential impact
The big idea is that this reasoning model often behaves like a skilled guesser that searches for a good “landing spot” in its hidden space. By giving it:
- better practice near solutions (data mixing),
- multiple perspectives on the same problem (input relabeling),
- and multiple slightly different brains (model bootstrapping),
you dramatically increase the chance it lands on the correct solution. Beyond Sudoku, this work suggests a new way to think about and improve “reasoning” AIs: don’t just make them think longer—help them make better and more diverse attempts, and teach them to hold onto correct answers once they find them.
Knowledge Gaps
Below is a single, concrete list of the paper’s unresolved knowledge gaps, limitations, and open questions that future work could address.
- Formal conditions for fixed-point stability: Specify and prove sufficient conditions (on architecture, training objective, and segment Jacobian norms) under which HRM learns true fixed points and preserves correct solutions across segments; characterize when the one-step gradient approximation is valid or fails.
- Theoretical link between one-step gradient and implicit models: Rigorously derive when substituting full BPTT with one-step gradients is unbiased or stable, and quantify the approximation error term involving across training and inference.
- Contractivity and local dynamics: Determine whether HRM segments are contractive near correct solutions (e.g., spectral radius of ) and design training or regularization to enforce local contractivity and fixed-point stability.
- Guaranteeing preservation of revealed tokens: Introduce and test constraints (e.g., masked-token preservation loss, projection layers, or hard constraints) that prevent corruption of unmasked input tokens; evaluate trade-offs with accuracy.
- Quantifying “grokking” triggers: Identify latent-state or loss-based signals that precede the sudden error drop; build predictors to time perturbations/early exiting; assess whether specific segment operations or activations precipitate leaps.
- Systematic mapping of attractor basins: Measure the prevalence, geometry, and sizes of basins of attraction for true vs spurious fixed points; estimate boundaries and switching dynamics across puzzles and training stages.
- Formalizing the latent “energy” landscape: Validate or refute the proposed conflict-count metric as the implicit objective optimized by segments; compare alternative differentiable surrogates; test whether making an auxiliary training target reduces spurious fixed points.
- Generalization beyond Sudoku: Test whether fixed-point violations, grokking dynamics, and spurious attractors persist on other reasoning tasks (mazes, math proofs, logic grids, program synthesis) and under different input modalities.
- Role of inner H/L modules: The paper obscures inner segment structure; perform ablations to determine whether observed phenomena (fixed-point violations, grokking) depend on or are mitigated by specific inner-module designs or coupling.
- ACT halting reliability: Quantify mis-halts (halting at spurious fixed points or failing to halt at correct ones), calibrate halting thresholds, and evaluate entropy- or confidence-based early exit criteria; assess accuracy–latency trade-offs.
- Data augmentation curriculum design: Identify which simplification schemes (mask ratios, structured vs random reveals, staged curricula) most effectively restore fixed points; optimize the mixing schedule and quantify diminishing returns.
- Input symmetry perturbations: Compare relabeling against other Sudoku symmetries (row/column swaps within bands, band/stack swaps, rotations/reflections); determine the minimal set yielding maximal diversity; study adaptive selection of transformations per-instance.
- Aggregation strategy for multiple passes: Evaluate alternatives to majority vote (weighted by confidence, score, ACT signals, or learned aggregators like product-of-experts) and measure improvements in accuracy and robustness.
- Model bootstrapping diversity: Assess whether ensembles of independent seeds (rather than adjacent checkpoints) yield larger gains; develop diversity metrics in parameter/activation space to select ensemble members; analyze compute–accuracy scaling.
- Direct latent-space perturbations: Develop structured or learned perturbations (low-rank subspace noise, Jacobian-informed nudges, normalizing flows) that preserve coherence while escaping spurious attractors; benchmark stability and success rates.
- Training-time regularizers for stability: Explore contractive mapping penalties, Lyapunov-based losses, or fixed-point consistency constraints (no-update once correct) to reduce drift and enforce stability in later segments.
- Full vs truncated BPTT comparisons: Empirically compare one-step gradient to truncated/full BPTT or implicit-layer training; measure impacts on fixed-point stability, grokking behavior, and accuracy under equal compute budgets.
- Quantitative taxonomy of reasoning modes: Provide frequencies of trivial/non-trivial success and failure across datasets; analyze correlations with puzzle difficulty, training stage, and segment count; use this to target failure mitigation.
- PCA visualization limitations: Validate latent trajectory interpretations with complementary methods (UMAP/t-SNE, linear probes, CCA across segments, local Lyapunov analyses); ensure consistent component bases across puzzles to avoid projection artifacts.
- Energy barrier generality: Test whether the observed “energy barrier” between rival attractors generalizes across many samples; quantify barrier heights and their relation to escape probabilities and number of segments needed.
- Computational efficiency of multi-pass methods: Characterize accuracy–compute trade-offs for input perturbation and model bootstrapping; design budgeted inference policies (best-of-k scheduling, early stopping on confidence) to approach 96.9% at lower cost.
- Sensitivity to dataset size/composition: Measure how performance and fixed-point stability scale with training set size, augmentation intensity, and puzzle diversity; identify minimal data regimes achieving stability.
- Calibration and confidence: Develop correctness confidence estimates (entropy, margin, agreement across passes) to detect spurious fixed points and to guide perturbation or halting decisions dynamically.
- Preventing overfitting to transformations: Confirm that symmetry-based augmentation does not induce brittleness or shortcut reliance; stress-test with adversarial transformation combinations and unseen symmetry patterns.
- Formal definition of “guessing vs reasoning”: Establish objective criteria/metrics (e.g., monotone loss trajectories, contribution of segments, causal interventions on latent states) to distinguish progressive reasoning from multi-start guessing behavior.
- Cross-task negative transfer: Investigate whether techniques that restore fixed points in Sudoku (e.g., data mixing, contractive losses) harm performance on other tasks; design task-agnostic stabilizers.
- Reproducibility details: Provide full training/inference hyperparameters, checkpoint selection rationale, augmentation settings, and code to enable replication of fixed-point violation detection and the 96.9% Augmented HRM result.
- Analysis of corruption of known tokens: Quantify how often and under what conditions unmasked inputs are altered; test adding hard copy-mechanisms or constraints to ensure input token invariance.
- Independence of multi-pass outputs: Measure correlation between outputs across input perturbations and checkpoints; develop theory for how much “intrinsic diversity” is needed to surpass pass@k-style sampling.
- Adaptive perturbation policies: Design policies that trigger perturbations only when certain signals (loss plateau, rising , halting uncertainty) are observed; evaluate reductions in unnecessary compute.
- Basin-aware initialization: Explore learned or heuristic initializers that bias toward true attractor basins; test meta-initialization or amortized inference methods that reduce time to solution.
- Integration with search: Compare latent-space multi-start HRM against explicit search methods (beam/MCTS over latent states) and hybrids; evaluate whether guided search reduces reliance on blind “guessing.”
- Robustness to noise and distribution shift: Stress-test Augmented HRM under noisy inputs, near-unsolvable puzzles, or altered rule sets; measure failure patterns and resilience of fixed-point stability.
Practical Applications
Overview
Below are actionable, real-world applications derived from the paper’s findings and methods. Each item specifies sector relevance, concrete use cases, potential tools/workflows, and key assumptions or dependencies that affect feasibility.
Immediate Applications
- Robust constraint-satisfaction solvers via “Augmented HRM” (software; games; operations research)
- Use case: Ship a production-ready Sudoku/KenKen/Kakuro/Crossword-fill solver that combines data mixing (near-solution training augmentation), input perturbations (symmetry-preserving relabelings/transformations), and checkpoint bootstrapping to dramatically raise exact solve rate.
- Tools/workflows: Inference wrapper that generates N relabeled inputs + M checkpoint runs with majority voting; training pipeline that injects “near-complete” instances to restore fixed-point stability.
- Assumptions/dependencies: Existence of valid equivalence transforms for the task; computing budget for multi-pass inference; access to raw checkpoints; tasks that admit stable fixed points.
- Scheduling and timetabling assistants with improved reliability (enterprise operations; logistics; education; healthcare operations)
- Use case: Staff rostering, university timetables, operating-room scheduling, and manufacturing job-shop scheduling framed as CSPs get higher solve rates by adopting Augmented HRM and multi-try inference.
- Tools/workflows: CSP preprocessor that auto-generates symmetry-equivalent formulations (e.g., resource relabelings, slot swaps) and ensembles them at inference; stability-tuning curriculum that mixes easy/hard subproblems during finetuning.
- Assumptions/dependencies: Problem symmetries are identifiable or can be programmatically synthesized; labels or verifiers exist to detect rule violations; compute cost is acceptable vs. business SLAs.
- Diversity-driven inference wrappers for existing iterative/recursive models (ML engineering; software)
- Use case: Wrap current latent-reasoning or recurrent solvers with standardized “multi-perspective” inference (input perturbation + checkpoint ensembles + majority vote), improving accuracy without retraining.
- Tools/workflows: Plug-in SDK that exposes transform libraries (relabel, rotate/reflect, band/row/column swaps for grid tasks; graph isomorphisms for graph tasks) and checkpoint orchestration.
- Assumptions/dependencies: Model determinism per pass; availability of semantically equivalent transformations; versioned checkpoints with similar quality.
- Fixed-point stability tests and diagnostics (ML reliability; interpretability)
- Use case: Add a CI test that feeds near-solved instances to validate the fixed-point property (answer should remain stable across segments). Catch regressions that cause “drift after correctness.”
- Tools/workflows: “Fixed-Point Stability Tester” that generates partially revealed instances and monitors segment-wise outputs; alerts when outputs flip after a correct segment.
- Assumptions/dependencies: Access to segment-level outputs and halting signals (ACT); tasks where “near-solved” examples can be created without leaking labels.
- Grokking/plateau detectors to allocate compute adaptively (ML systems; cloud cost optimization)
- Use case: Detect per-instance plateaus in segment-wise loss/consistency; trigger a restart with input perturbation or checkpoint switch rather than spending more segments; early exit when stabilized.
- Tools/workflows: “Early-Exit Controller” that monitors surrogate progress metrics (e.g., conflicts counter or output entropy) and orchestrates retries/perturbations.
- Assumptions/dependencies: Availability of a fast verifier or conflict metric; ACT hooks; tolerance for multiple short runs instead of one long run.
- Interpretability dashboards for latent trajectories (R&D; education)
- Use case: Visualize PCA/UMAP-projected latent paths to reveal “trap” attractors, sudden leaps (“grokking”), and symmetry restoration after data mixing; use in debugging and teaching.
- Tools/workflows: “Latentscape Analyzer” that records zi, overlays conflict heatmaps, and flags rival attractors.
- Assumptions/dependencies: Access to latent states; privacy constraints permit logging latent activations.
- Benchmarking and evaluation upgrades for reasoning robustness (industry standards; policy in ML evaluation)
- Use case: Require reporting robustness under symmetry-equivalent inputs and multi-checkpoint ensembles; include near-solution robustness scores and fixed-point stability rates in leaderboards.
- Tools/workflows: Evaluation harness that auto-applies equivalence transforms, aggregates pass@k-like metrics tailored to deterministic latent models, and logs segment-wise behavior.
- Assumptions/dependencies: Community adoption; curated transform sets per domain.
- Puzzle apps and consumer tools with “try-many-views” reasoning (consumer software; daily life)
- Use case: Mobile puzzle solvers that invisibly relabel/transform the puzzle multiple ways to raise solve success and speed; expose a “retry different perspective” button.
- Tools/workflows: Lightweight inference ensemble with time/energy caps; on-device caching of diverse perspectives.
- Assumptions/dependencies: Energy/latency budgets; small model size or efficient on-device ensembling.
Long-Term Applications
- General CSP and optimization engines powered by latent-space ensembles (software; operations research; energy; telecom)
- Use case: Vehicle routing, network routing, grid scheduling, and resource allocation solved by HRM-like models augmented with systematic perturbations, rival-attractor avoidance, and fixed-point curricula.
- Tools/workflows: “Reasoning Ensemble Orchestrator” that learns domain-specific equivalence transforms (graph isomorphisms, factor rotations, resource relabelings) and manages checkpoint/model diversity.
- Assumptions/dependencies: Transferability of HRM insights beyond Sudoku; scalable verifiers; safety and cost constraints for multi-pass reasoning at industrial scale.
- Robotics and autonomous planning with multi-attractor-aware controllers (robotics; autonomy)
- Use case: Planners that recognize when they are trapped in spurious attractors (locally consistent but globally wrong plans) and proactively switch viewpoint (relabel objects/frames) or policy checkpoints.
- Tools/workflows: Controller that monitors latent conflict metrics or plan-inconsistency signals; “checkpoint bootstrapper” for planners trained with different seeds/curricula; ACT-like compute control.
- Assumptions/dependencies: Reliable surrogate metrics for plan correctness; safety certification for perturbation-based retries.
- Program synthesis, formal methods, and theorem proving via stabilized latent reasoning (software engineering; verification)
- Use case: Neural provers/synthesizers that train with near-solution subgoals to enforce fixed points; during inference, use input perturbations (symbol renaming/alpha-conversion, goal reordering) and ensemble checkpoints to avoid false proofs.
- Tools/workflows: Data mixing over partial proofs; “equivalence transform” libraries for logic/ASTs; ensemble orchestration with majority or proof-checker voting.
- Assumptions/dependencies: Strong verifiers/checkers to validate outputs; scalable transform libraries for code/logic.
- Clinical and operational decision support with multi-hypothesis exploration (healthcare ops; public sector)
- Use case: For complex, rule-constrained workflows (bed management, referral routing, OR block allocation), deploy latent reasoning with structured retries across symmetry-equivalent formulations; exploit curricula to stabilize near-feasible solutions.
- Tools/workflows: Human-in-the-loop verifier interfaces; robust audit trails of retries and chosen hypotheses.
- Assumptions/dependencies: Regulatory approvals; rigorous safety constraints; clear objective/constraint definitions.
- Finance and portfolio construction under constraints (finance)
- Use case: Constraint-rich portfolio optimization and risk-parity allocations where false attractors correspond to locally consistent yet suboptimal allocations; apply factor/asset relabeling, checkpoint ensembles, and near-solution curriculum.
- Tools/workflows: Adapter that produces symmetry-equivalent factorizations (e.g., rotations of factor bases) and aggregates solutions subject to risk/return verifiers.
- Assumptions/dependencies: Reliable, domain-appropriate equivalence transformations; robust backtesting and risk controls.
- Scientific design under constraints (materials/molecules; bioengineering)
- Use case: Generate candidates that satisfy complex discreto-structural constraints (valency, symmetry, motifs); use perturbation-based retries and ensembles to escape chemically plausible but incorrect attractors.
- Tools/workflows: Domain verifiers (e.g., rule-based or simulator-in-the-loop); curricula with partial/near-valid scaffolds.
- Assumptions/dependencies: Accurate verifiers; scalable training data of diverse “difficulty”; alignment with physical feasibility.
- Standards and governance for reasoning model safety (policy; standards bodies)
- Use case: Define guidance that distinguishes “guessing” from “reasoning” in iterative models; mandate tests for fixed-point stability, robustness to symmetry transforms, and transparency of multi-pass strategies in safety-critical deployments.
- Tools/workflows: Compliance test suites and reporting schemas for segment-wise stability, multi-attractor sensitivity, and ensemble behaviors.
- Assumptions/dependencies: Multi-stakeholder agreement; domain-specific safety cases; availability of open test artifacts.
Notes on feasibility across applications:
- Dependencies that help: identifiable equivalence transformations; cheap verifiers (rule-checkers); access to segment-wise outputs/ACT; ability to run small ensembles; curricula that include easier subproblems to restore fixed-point stability.
- Risks/constraints: compute overhead of multi-pass inference; absence of symmetries in some domains; potential overfitting to transforms; need for rigorous verifiers in safety-critical contexts; unknown generalization from Sudoku to other complex tasks without domain-tailored designs.
Glossary
- Adaptive computation time (ACT): A mechanism that adaptively decides whether to continue or stop computation in a recursive model based on progress. "an adaptive computation time (ACT) mechanism~\cite{graves2017adaptivecomputationtimerecurrent} is introduced to decide whether to halt the computation after each segment."
- Attractor: A point in state space toward which the model’s latent dynamics converge; can be correct or misleading. "there appear to be two attractors (left: correct; right: misleading), the interaction between which create a clear boundary of two regions."
- Backpropagation through time (BPTT): The training method for recurrent-like models that propagates gradients through sequential steps. "the computation required for one back propagation through time (BPTT)~\cite{Rumelhart1986LearningIR, werbos1990bptt} of all these segment losses scales at "
- Band (Sudoku): A group of three adjacent rows (or columns) in Sudoku used in symmetry-preserving transformations. "Such transformations include relabeling the tokens, swapping bands, swapping rows or columns within a band, and reflecting/rotating the entire puzzle."
- Chain-of-thought (CoT) prompting: A technique that elicits step-by-step reasoning by generating intermediate textual thoughts. "It either relies on chain-of-thought (CoT) prompting~\cite{wei2023chainofthoughtpromptingelicitsreasoning, chen2025survey} or fine-tuning with reinforcement learning~\cite{guo2025deepseek,wen2025reinforcement,yue2025does}"
- Deep supervision: A training strategy that applies losses to intermediate states/outputs to enable reasoning depth scaling. "The core training technique to achieve reasoning depth scaling is deep supervision~\cite{wang2025hierarchicalreasoningmodel}."
- Energy barrier: An increase in an energy-like metric that impedes transition between states, indicating non-monotonic difficulty. "The ridge shows that this metric is non-monotonic (has an “energy barrier”) between the rival attractors."
- Energy function: A label-agnostic scalar objective hypothesized to be implicitly minimized, e.g., measuring conflicts in outputs. "We hypothesize that the segment dynamics of HRM are implicitly doing minimization on some (label-agnostic) energy function, measuring ‘how good the current output is’ by counting conflicts."
- Fixed point property: The assumption that once the correct latent state is found, further updates leave it unchanged. "HRM theory assumes the fixed point property, i.e., the ability to maintain stability after finding the solution;"
- Grokking: A sudden transition from failure or plateau to success after prolonged training or recursion. "Per-sample analysis shows “grokking” dynamics along segments."
- Heuristic error metric: A problem-specific measure (e.g., conflict count) used to evaluate output quality without labels. "We show that these false attractors can be interpreted as local optima of a heuristic error metric measuring the number of conflicts."
- Implicit models: Models defined via fixed-point conditions or implicit relations where gradients are approximated without full unrolling. "as long as $I-\left.J_{\mathcal{F}\right\rvert_{z^*} \approx I$ (a common approximation for implicit models)"
- Input perturbation: Modifying inputs via symmetry-preserving transformations to explore different latent trajectories and guesses. "input perturbation (scaling the number of guesses by leveraging inference randomness)"
- Latent-space reasoning model: A model that performs reasoning by evolving continuous hidden representations rather than explicit tokens. "latent-space reasoning models~\cite{hao2025traininglargelanguagemodels, wang2025hierarchicalreasoningmodel} rise as a new paradigm of reasoning depth scaling."
- Local minima: Suboptimal minima in a nonconvex landscape that can trap optimization dynamics. "In nonconvex optimization, gradient methods are susceptible to being trapped by local minima."
- Majority vote: Aggregating multiple model runs by selecting the most frequent outcome among successful halts. "a majority vote is done among those that successfully halted."
- Mean-field analysis: An averaging-based perspective to study loss scaling laws across samples. "Mean-field Analysis: Scaling Laws of Loss Curves"
- Model bootstrapping: Leveraging diversity across training checkpoints to produce multiple distinct guesses. "model bootstrapping (scaling the number of guesses by leveraging training randomness)"
- Nonconvex optimization: Optimization over landscapes with multiple basins, saddles, and local minima. "In nonconvex optimization, gradient methods are susceptible to being trapped by local minima."
- One-step gradient: A training method computing gradients only for the current segment, detaching previous states. "a dual technique called one-step gradient~\cite{wang2025hierarchicalreasoningmodel} is used: during optimization, the gradient of is only computed with respect to the -th segment."
- Outer loop: The top-level recursion over segments in HRM’s forward pass. "allowing us to focus mainly on the outer loop."
- Pass@k: An evaluation protocol that considers success across multiple independent attempts, commonly in code LLMs. "these methods are essentially different from pass@k~\cite{chen2021evaluatinglargelanguagemodels} used in LLM evaluation."
- Principal component analysis (PCA): A dimensionality reduction method used to visualize latent trajectories. "projecting them onto the plane defined by their first two PCA components."
- Spurious fixed point: A stable but incorrect latent state that traps the model away from the true solution. "spurious fixed points being malignant attractors."
Collections
Sign up for free to add this paper to one or more collections.