Reasoning Models Reason Well, Until They Don't (2510.22371v1)
Abstract: LLMs have shown significant progress in reasoning tasks. However, recent studies show that transformers and LLMs fail catastrophically once reasoning problems exceed modest complexity. We revisit these findings through the lens of large reasoning models (LRMs) -- LLMs fine-tuned with incentives for step-by-step argumentation and self-verification. LRM performance on graph and reasoning benchmarks such as NLGraph seem extraordinary, with some even claiming they are capable of generalized reasoning and innovation in reasoning-intensive fields such as mathematics, physics, medicine, and law. However, by more carefully scaling the complexity of reasoning problems, we show existing benchmarks actually have limited complexity. We develop a new dataset, the Deep Reasoning Dataset (DeepRD), along with a generative process for producing unlimited examples of scalable complexity. We use this dataset to evaluate model performance on graph connectivity and natural language proof planning. We find that the performance of LRMs drop abruptly at sufficient complexity and do not generalize. We also relate our LRM results to the distributions of the complexities of large, real-world knowledge graphs, interaction graphs, and proof datasets. We find the majority of real-world examples fall inside the LRMs' success regime, yet the long tails expose substantial failure potential. Our analysis highlights the near-term utility of LRMs while underscoring the need for new methods that generalize beyond the complexity of examples in the training distribution.
Summary
- The paper demonstrates that large reasoning models perform well on simple tasks but rapidly fail as reasoning complexity increases.
- Methodology employs the DeepRD benchmark with controlled lookahead and branching metrics to assess both symbolic queries and natural language proof planning.
- Error analysis identifies propagation errors like omitted or hallucinated edges, highlighting challenges for multi-step reasoning in real-world applications.
Limits of Large Reasoning Models: Performance Collapse at High Complexity
Introduction
The paper "Reasoning Models Reason Well, Until They Don't" (2510.22371) presents a systematic investigation into the reasoning capabilities of Large Reasoning Models (LRMs)—LLMs fine-tuned for stepwise argumentation and self-verification—on tasks with scalable complexity. The authors introduce the Deep Reasoning Dataset (DeepRD), a synthetic benchmark designed to probe reasoning depth and branching factor, and analyze LRM performance on both symbolic graph connectivity and natural language proof planning. The paper reveals that while LRMs excel on low-complexity tasks, their performance collapses abruptly as problem complexity increases, with implications for the deployment of LLMs in real-world, reasoning-intensive domains.
Figure 1: An example from DeepRD, illustrating a graph with lookahead and number of branches , rendered as both a symbolic graph query and a natural language proof planning prompt.
Complexity Metrics and Dataset Construction
The authors formalize reasoning complexity using two metrics: lookahead (), the number of BFS iterations required to determine the next correct node in a path, and number of branches (), the out-degree of the start node. These metrics allow precise control over the difficulty of synthetic reasoning tasks. DeepRD is generated via a parameterized process that produces directed acyclic graphs (DAGs) with specified and , avoiding isomorphisms and ensuring unique solution paths. Each graph is rendered both as a symbolic connectivity query and as a natural language proof planning prompt, enabling cross-modal evaluation.
Model Evaluation: Graph Connectivity
LRMs (DeepSeek-R1, o3-mini, o3) and baseline LLMs (DeepSeek-V3, GPT-4o) are evaluated on NLGraph-hard and DeepRD. On NLGraph-hard, LRMs achieve near-perfect accuracy, outperforming LLMs and chain-of-thought/self-consistency prompted baselines. However, NLGraph-hard examples have low lookahead (1.8), limiting their diagnostic value.
Figure 2: Full path accuracy for V3, R1, 4o, o3-mini, and o3 on DeepRD graph connectivity tasks, as a function of and .
On DeepRD, as increases, all models exhibit a sharp drop in accuracy, with the collapse occurring at lower for higher . LRMs maintain higher accuracy than LLMs at moderate , but ultimately fail to generalize beyond the complexity seen in training. Notably, even in chain graphs (), where the task is trivial, performance degrades rapidly with increasing depth.
Figure 3: Full path accuracy for chain graphs () as a function of graph depth, showing rapid performance collapse even in the absence of search complexity.
Token usage analysis demonstrates that performance collapse is not attributable to context length or truncation; LRMs rarely hit token limits, and completion token usage decreases with increasing .
Figure 4: Average token completion count for and between 2 and 800, indicating that token limits do not explain accuracy drops.
Model Evaluation: Proof Planning
The same graphs are rendered as natural language proof planning tasks, where models must predict the next step in a deductive chain. The performance cliffs observed in symbolic graph reasoning persist, with accuracy collapsing at even lower than in the symbolic setting. Residual accuracy at high and matches the $1/B$ chance level, indicating stochastic guessing rather than genuine reasoning.
Figure 5: Next step prediction accuracy for proof planning tasks, as a function of and .
Error Analysis and Failure Modes
Manual inspection of LRM "thinking tokens" reveals three dominant error types: omission of necessary edges, failure to consider all branches, and hallucination of nonexistent edges. These errors propagate through the reasoning chain, leading to locally consistent but globally incorrect solutions. The analysis aligns with prior work on "propagation errors" in transformers, where early local mistakes undermine global correctness as depth increases.
Real-World Complexity Distributions
The authors compute lookahead and branching distributions for large real-world graphs (ConceptNet, ogbl-wikikg2, ogbn-papers100M, NaturalProofs). Most real-world queries fall within the LRMs' success regime, but the long tail of high-complexity instances lies beyond current model capabilities.
Figure 6: Histograms of lookahead and number of branches for real-world datasets, with percentile markers indicating the regime where LRM performance collapses.
Verification of Real-World Proofs
LRMs are evaluated on error detection in the NaturalProofs dataset, using minimally perturbed proof lines. Error detection accuracy drops precipitously as proof length increases, mirroring the synthetic results and confirming that depth-sensitive failure is not an artifact of synthetic data.
Figure 7: Error detection accuracy with respect to proof length when a single perturbation is introduced, showing dramatic performance collapse.
Figure 8: Error detection accuracy on unperturbed proofs, indicating that performance drop is not solely due to perturbation.
Implications and Future Directions
The findings demonstrate that current LRMs are tightly bound to their training distribution and do not exhibit robust generalization to high-complexity reasoning tasks. This has direct implications for the deployment of LLMs in domains requiring deep, multi-step reasoning, such as scientific discovery, mathematics, and law. The DeepRD framework enables controlled evaluation and future research into methods for improving out-of-distribution generalization, such as curriculum learning, architectural modifications, or explicit search mechanisms.
Conclusion
The paper establishes that LRMs, despite impressive performance on low-complexity benchmarks, fail abruptly as reasoning complexity increases. The DeepRD dataset provides a scalable testbed for probing these limits and highlights the necessity for new approaches to achieve robust, human-like reasoning in LLMs. Bridging the gap between current capabilities and the demands of real-world, long-tail reasoning tasks remains a critical challenge for the field.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper asks a simple but important question: Can today’s AI “reasoning” models keep reasoning well as problems get harder, or do they suddenly fail? The authors build a new test set to steadily make reasoning tasks more complex and then check how different AI models perform as the difficulty rises.
In short: Reasoning models look great on easy and medium problems—but their performance drops off a cliff once the problems get complex enough.
What questions did the authors ask?
The authors focused on three easy-to-understand questions:
- How does AI performance change as graph problems get more complex?
- How does AI performance change as natural-language proof problems get more complex?
- How complex are real-world problems compared to what these models can actually handle?
How did they test this?
To measure reasoning fairly, the authors used two related tasks and a way to control how hard each example is.
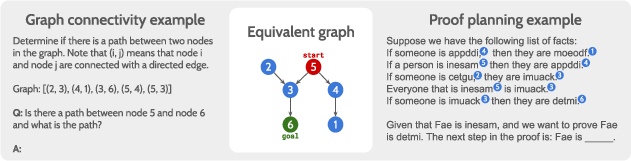
- Task 1: Graph pathfinding
- Imagine a map of cities (called “nodes”) connected by roads (called “edges”).
- The question: Is there a route from Start City to Goal City? If yes, what is the next step or the full path?
- Task 2: Natural-language proof planning
- The input is a list of simple “if A then B” facts (like “If someone is a cat, then they are a mammal”).
- The question: Given a starting fact and a goal fact, what is the next correct step toward proving the goal?
- This is really the same as the graph task, but written in everyday language: each fact is like a road, and each statement is like a city.
To control difficulty, they used two simple ideas:
- Lookahead (L): How many rounds of “peeking ahead” you must do to be sure which next step is correct. Think of it like standing at a fork and needing to look 2, 10, or 100 steps ahead to know which path eventually reaches the goal.
- Branches (B): How many choices you have at the current step (like how many roads leave this intersection). More branches means more chances to go wrong.
They built a new dataset called DeepRD that lets them generate unlimited problems with exact control over L and B:
- They tested models on L ranging from small (like 2) to very large (like 800), and B from 1 (a single straight road) to 16 (many choices).
- They tested both graph and natural-language proof versions of the same underlying problems.
They also checked real-world data (like big knowledge graphs and proof collections) to see how complex real problems are and how that compares to what models can handle.
Finally, they tested several well-known AI models:
- “LRMs” (Large Reasoning Models) trained to show their steps and self-check: DeepSeek R1, OpenAI o3-mini (and some tests on full o3)
- Regular “LLMs” (LLMs) without special reasoning training: DeepSeek V3, GPT-4o
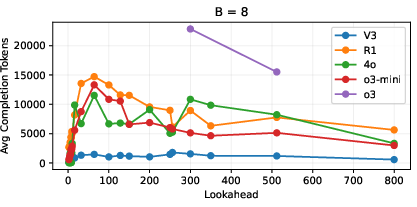
They also made sure failures weren’t just because the models ran out of space (token limits) by tracking how many tokens the models used. They found the failures weren’t caused by length limits.
What did they find?
Here are the main results, in plain terms:
- On existing benchmarks that look big but are actually easy (low lookahead), LRMs do great. This can make it seem like they’ve mastered reasoning.
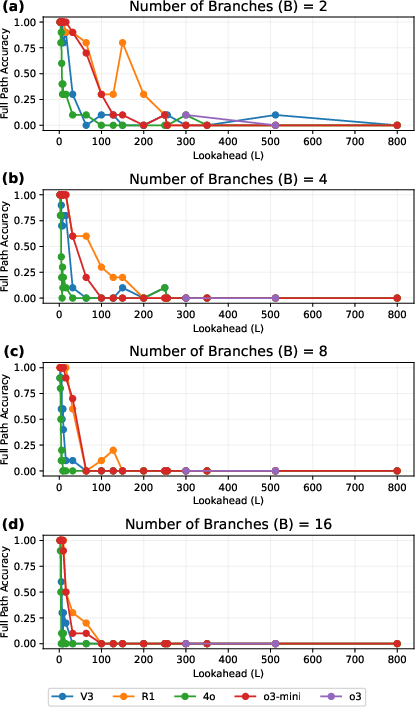
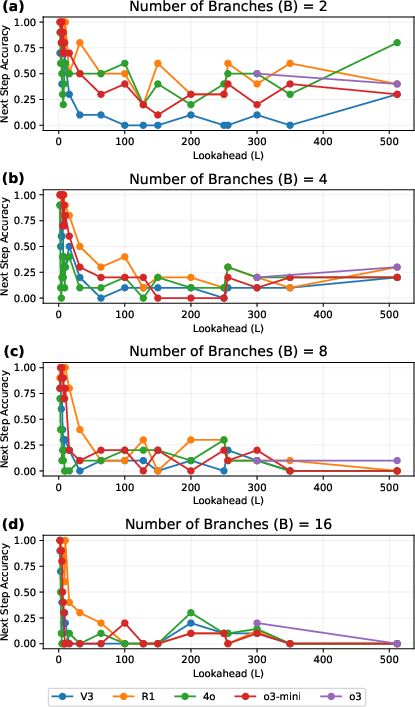
- But when the authors carefully scale up complexity (higher L and/or more branches B), performance suddenly collapses:
- All models, including the reasoning-tuned ones, hit a “cliff” where accuracy drops sharply to near zero once L and B get large enough.
- This drop happens earlier when there are more branches (more choices).
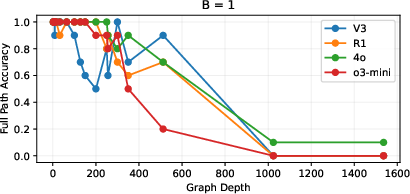
- Even when there’s only one road forward (B = 1)—the easiest possible kind of graph—the models still fail once the path is long enough. So the problem isn’t just picking among many options; it’s sustaining correct reasoning over long chains.
- In natural-language proof planning, the collapse happens even earlier than in the graph version. When B is big, models often fall back to guessing:
- With 2 choices, random guessing gives 1/2 accuracy.
- With 4 choices, random guessing gives 1/4 accuracy.
- The models’ accuracy often hovers around these “chance” levels at high complexity, which means they’re not really reasoning—they’re guessing.
- The failures are not due to token limits. In fact, for harder cases, the models often use fewer tokens, and the collapse still happens.
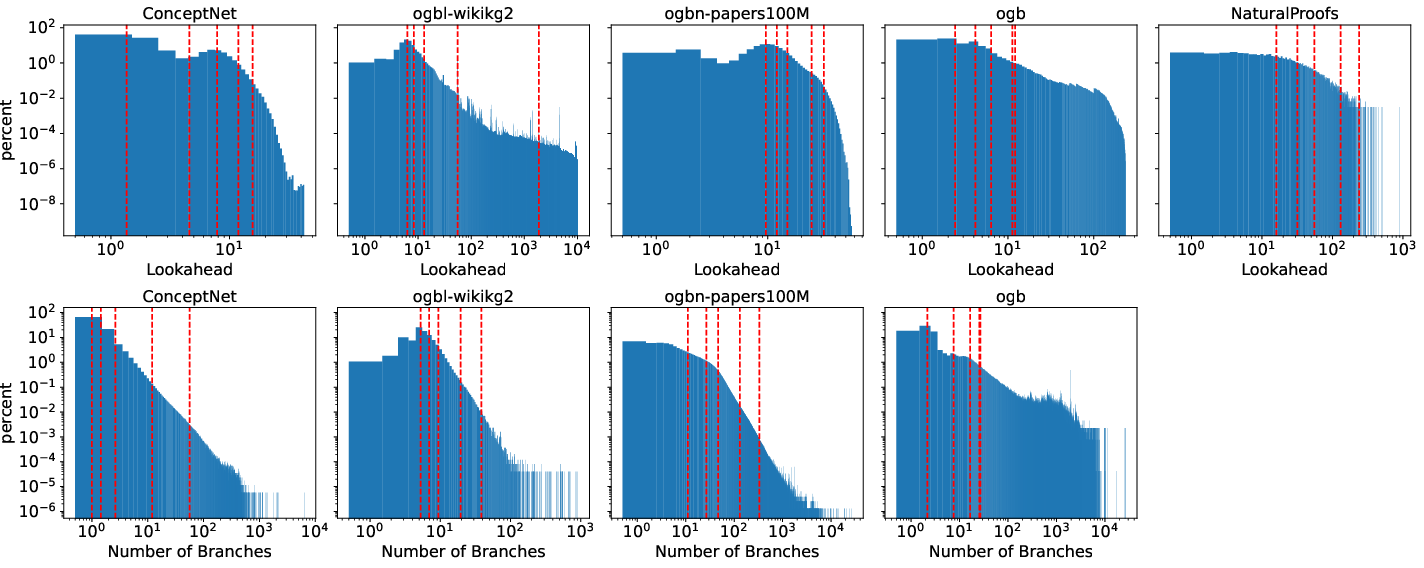
- When checking real-world datasets (knowledge graphs and proof corpora), most problems are relatively simple and fall inside the “safe zone” where models do well. But there’s a long tail of hard cases where lookahead and branching explode—and that’s exactly where models fail badly.
- Common failure modes (from looking at the models’ internal “thinking” logs) include:
- Missing an available road (edge) that’s actually listed,
- Ignoring one branch entirely,
- Imagining (hallucinating) a road that doesn’t exist.
- A small early mistake often “propagates” through the rest of the reasoning and ruins the final answer.
Why this matters:
- The models’ strong performance on currently popular benchmarks may be misleading because those benchmarks don’t push complexity very far.
- In real life, there are many simple queries (where models will look great) but also important hard ones (where they can fail unexpectedly).
Why does it matter?
- Near-term usefulness: LRMs are very helpful on lots of everyday problems that don’t require deep, branching reasoning. That’s good news for many practical uses like simple Q&A, short proofs, and small graph tasks.
- Limits on deep reasoning: When problems require long chains of logic or many alternative paths, current models don’t generalize well and can break suddenly. That’s risky for high-stakes tasks in science, medicine, law, and complex planning.
- Better tests and training needed: We need new methods that truly teach models to handle harder reasoning—and new benchmarks (like DeepRD) that steadily scale difficulty to reveal where models actually stand.
In one sentence: These models reason well—until they don’t. DeepRD shows exactly where and why they fall off, and it gives researchers a tool to build models that can go deeper without collapsing.
Knowledge Gaps
Unresolved gaps, limitations, and open questions
Below is a single, concrete list of what remains missing or unexplored, designed to be directly actionable for future research.
- Complexity metrics are narrowly defined (lookahead L and branching B); extend to cyclic graphs, multi-relational/typed edges, weighted edges, dynamic graphs, and alternative structural complexities (e.g., diameter, path multiplicity, trap states, distractor density).
- Input encoding is fixed to a particular textual format; systematically ablate graph encodings (edge lists vs adjacency, canonicalization, ordering, separators, node naming) and quantify sensitivity.
- Output-path extraction uses a secondary LLM (GPT‑4o‑mini) without auditing; measure extraction error, robustness to formatting variance, and its effect on accuracy estimates.
- Proof planning is evaluated only as “next-step” prediction; test full end-to-end proof generation, iterative step-by-step planning with verification, and formal tooling integration (e.g., Lean checkers).
- The NaturalProofs perturbation pipeline is noisy; build cleaner, controlled perturbations with guaranteed semantic changes and provide human-verified gold labels and baselines.
- Real-world graph complexity is summarized via pairwise node lookaheads; evaluate task-specific query distributions (e.g., multi-hop QA neighborhoods) rather than uniform node pairs to better reflect deployed workloads.
- For proofs, branching is treated as “effectively infinite”; develop operational branching measures (e.g., admissible inference fan-out under a fixed rule set and premise budget).
- Token-limit conclusions are based on stop_reason inspection and average usage; perform controlled experiments varying max_tokens, scratchpad budgets, and context window sizes to isolate working-memory vs planning failures.
- The observed “1/B” accuracy plateau is inferred; verify by controlled interventions (e.g., disabling chain-of-thought, forcing single-token answers, or explicit random-choice prompts) to confirm stochastic guessing.
- Failure-mode analysis is limited in sample size and model coverage (R1 only); scale to thousands of traces across models (including o3/o3‑mini) and quantify error-type prevalence as a function of L, B, and encoding.
- Strong sensitivity to input order is noted (near-perfect accuracy when edges are in traversal order) but not characterized; measure invariance to permutations and design order-robust prompts or encodings.
- DeepRD sampling provides only 10 examples per (L,B) cell; increase per-cell sample sizes, report confidence intervals, and perform power analyses to ensure statistical reliability of cliff locations.
- Contamination claims (synthetic DAGs) are stronger for symbolic graphs than for natural-language proofs; conduct leakage scans against public pretraining corpora and common template libraries used for NL inference.
- No ablations on decoding settings (temperature, top_p, top_k, repetition penalties); quantify how sampling strategy affects reasoning depth, hallucinations, and plateau behavior.
- Tool-augmented reasoning (code execution, graph DB queries, BFS planners) is not evaluated; test whether tool use mitigates cliffs and under what latency/cost trade-offs.
- Algorithmic prompting (explicit BFS/DFS plans, agenda-based search, frontier caching) is not explored; evaluate whether structured search templates reduce early local missteps and propagation errors.
- Calibration is unmeasured; assess whether models can detect when they are in the “tail” (high L/B) and abstain or defer to tools, and whether confidence correlates with correctness.
- Cross-lingual robustness and domain breadth are untested; extend to multilingual proofs, math-heavy corpora, biomedical reasoning with typed relations, and law contracts, measuring complexity-specific performance.
- No comparison to non-LLM baselines (GNNs, classical planners, theorem provers); establish reference curves to contextualize LLM/LRM failures and identify hybrid designs that surpass LLM-only cliffs.
- No scaling-law modeling of cliff transitions; fit parametric models to predict accuracy as a function of L, B, token budget, and prompt length, and identify regime boundaries.
- o3/o3‑mini internal “thinking” tokens are unavailable; prioritize instrumentation or proxy methods (e.g., forced scratchpad logging) to enable cross-model failure analysis.
- Iterative next-step prompting to build full paths/proofs (compounding errors, recovery) is not evaluated; measure cumulative accuracy, error recovery strategies, and the value of backtracking.
- Error propagation mitigation strategies (structured caches, premise tracking, pointer/reference mechanisms) are not tested; evaluate designs that keep consistent state across deep reasoning.
- Real-world graph lookahead estimates rely on node sampling; quantify sampling bias, provide variance/CI on percentiles, and validate against exhaustive computations where feasible.
- Edge hallucination rates are reported but not causally connected to specific behaviors; distinguish copy errors, search failures, and formatting mismatches, and test targeted mitigations.
- Model refusals and API constraints are excluded from accuracy; analyze refusal rates by complexity, their causes (safety, budget), and their impact on practical deployment.
- Fine-tuning on DeepRD high-complexity regimes is proposed but not executed; run controlled fine-tuning and test transfer to natural-language proofs and real-world graphs, including out-of-distribution generalization.
- Prompting strategies (few-shot, structure-aware demonstrations, self-consistency, retrieval) are not systematically varied for LRMs; ablate these to see if cliffs move or soften.
- The mapping from symbolic graphs to NL facts may be template-biased; diversify linguistic realizations (paraphrases, coreference, negation, quantifiers) and measure semantic robustness at high L/B.
Practical Applications
Practical Applications Derived from the Paper
The paper introduces DeepRD (a controllable generator and dataset for scalable reasoning complexity), demonstrates abrupt failure modes of Large Reasoning Models (LRMs) beyond modest complexity, and quantifies real-world complexity distributions that include significant long-tail risks. Below are actionable applications, grouped by time horizon, with sector links, potential tools/workflows, and feasibility notes.
Immediate Applications
The following can be deployed now using current models, the released DeepRD generator, and standard orchestration frameworks.
- Complexity stress-testing and model certification
- Sectors: software (AI vendors), enterprise AI governance, procurement, standards bodies.
- What: Use DeepRD to benchmark LLMs/LRMs under controlled lookahead L and branching B, publish “complexity profile” reports (e.g., accuracy plateaus for L≤32 in natural language proofs; L≈100–200 for symbolic connectivity; B sensitivity).
- Tools/products: DeepRD Benchmark Kit; CI/CD gate for “pass/fail by complexity tier”; vendor evaluation rubric.
- Assumptions/dependencies: Access to model APIs and DeepRD; internal policy to require stress-tests; compute budget for batch runs.
- Complexity-aware task routing in LLM orchestration
- Sectors: software platforms, customer support automation, developer copilots, data analytics.
- What: Estimate problem complexity (approximate lookahead/branching) at runtime and route:
- Low L/B → LRM/LLM with CoT/self-verification.
- Moderate/High L or B → external algorithmic solvers (e.g., BFS/DFS over graphs, formal verifiers) or human-in-the-loop.
- Tools/workflows: “Complexity Sentinel” middleware that:
- Maps tasks to graph-like structures (dependency DAGs, KG paths).
- Computes/estimates L and B (heuristics, sampling).
- Switches to programmatic graph search, SPARQL/Gremlin, or theorem provers when thresholds are exceeded.
- Assumptions/dependencies: Availability of graph backends or verifiers; task-to-graph adapters; latency tolerance for routing.
- Guardrails for knowledge-graph question answering
- Sectors: search/QA, enterprise knowledge management.
- What: For KG QA, cap reliance on LLM path-finding beyond a threshold (e.g., L>64 or B>4) and default to deterministic path algorithms; require model-produced paths to be validated against the KG before finalizing answers.
- Tools/products: KG-aware router; path validator; SPARQL/Gremlin executors; edge-hallucination checkers (given high hallucination rates observed).
- Assumptions/dependencies: KG access; transformation of NL queries to graph queries; performance budgets.
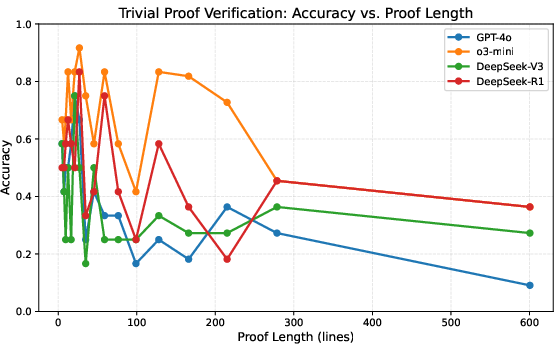
- Proof-assistance with depth-aware verification
- Sectors: education (STEM tutoring), software (formal methods), law (argument structuring), scientific writing.
- What: Use LRMs for local inference steps but impose:
- Depth caps for end-to-end plans (given collapse ≈16–32 steps).
- Mandatory verification via formal provers (Lean, Coq, Isabelle) or rule checkers when proofs exceed caps.
- Tools/workflows: “Next-step suggester” integrated with formal verifiers; chunked proof planning with windowed validation; error-line locator (mirroring the NaturalProofs perturbation setup).
- Assumptions/dependencies: Access to formal systems; proof formalization or weakly formal templates; acceptance of partial proofs/hints.
- MLOps monitoring of encountered complexity
- Sectors: enterprise AI ops, safety/risk teams.
- What: Telemetry that logs estimated L/B for real user queries and correlates with error rates; trigger escalation when tail complexity spikes.
- Tools/products: Complexity dashboards; drift alerts when traffic distribution shifts toward higher L/B; auto-escalation policies.
- Assumptions/dependencies: Instrumentation to compute proxies for L/B; privacy-safe logging.
- Data and training curriculum design
- Sectors: model providers, research labs, applied ML teams.
- What: Use DeepRD to generate controllable curricula that scale depth and branching; measure transfer from symbolic (graphs) to natural language proof planning.
- Tools/products: Depth/branching curriculum generator; evaluation harness; error taxonomy (omission, missed branch, hallucinated edge) to guide fine-tuning.
- Assumptions/dependencies: Training budget; capacity to run ablations on curricula; alignment with licensing constraints.
- Safety policies and escalation criteria in regulated domains
- Sectors: healthcare (clinical decision support), finance (risk analysis), legal (compliance).
- What: Define complexity thresholds beyond which automated decisions are disallowed without human review; log provenance and verified paths for audit.
- Tools/workflows: Decision policies tied to complexity estimates; human-review queues; provenance capture (record of graph paths and verifications).
- Assumptions/dependencies: Governance frameworks; clear SLAs and audit requirements; integration with existing workflow tools.
- Education: teaching reasoning limits and robust methods
- Sectors: higher education, professional training.
- What: Classroom labs illustrating performance cliffs; assignments using DeepRD to compare CoT vs. algorithmic search; pedagogy on neuro-symbolic hybrids.
- Tools/products: Course modules; notebooks; graded complexity exercises.
- Assumptions/dependencies: Instructor adoption; student compute.
- Cost control and model selection
- Sectors: software, platform ops.
- What: Prefer LRMs for shallow tasks; switch to cheaper LLMs or deterministic solvers when L/B predicts failure or random guessing; set token budgets knowing token limits are not the driver of failures.
- Tools/workflows: Cost-aware routers; concise-output prompting (avoid spurious “chance-level wins” that mask failure).
- Assumptions/dependencies: Telemetry on accuracy vs. complexity; prompt libraries.
- Robotics and planning with hybrid controllers
- Sectors: robotics, operations research, process automation.
- What: For short-horizon plans, use LRMs; for longer horizons/branching, delegate to classical planners (A*, MCTS) with LLM for natural language grounding/explanations.
- Tools/workflows: Planning router; explanation layer that converts planner outputs to NL.
- Assumptions/dependencies: Simulator/planner integration; latency bounds.
Long-Term Applications
These require further research in generalization, architecture, or tooling maturity.
- Neuro-symbolic reasoning systems that scale beyond training complexity
- Sectors: software, scientific computing, autonomous research.
- What: Architectures that combine LLMs with explicit search/planning/verification modules to maintain correctness at high L and B (e.g., learned controllers over BFS/DFS, theorem provers, constraint solvers).
- Tools/products: Reasoning kernels co-executed with LLMs; verifier-first decoders; proof-carrying responses.
- Assumptions/dependencies: Advances in interfaces between neural policies and symbolic engines; efficient verifier APIs; training on mixed modalities.
- Depth-aware RL with verifiable rewards at scale
- Sectors: model providers, academia.
- What: New post-training that rewards success at increasing depth/branching, with curriculum schedules and breadth-aware task samplers; penalties for propagation errors and edge hallucinations.
- Tools/workflows: Depth-conditioned reward functions; scalable verification oracles; synthetic-to-natural transfer pipelines.
- Assumptions/dependencies: Stable training regimes; affordable verification at scale; mitigation of overfitting to generator artifacts.
- Universal complexity estimators for NL tasks
- Sectors: platform orchestration, evaluation science.
- What: Methods to map arbitrary NL problems to latent DAGs and estimate lookahead/branching without explicit graphs; uncertainty-aware thresholds to drive routing.
- Tools/products: Task-to-DAG mappers; proxy metrics (e.g., retrieval graph diameter, dependency distance); calibration tooling.
- Assumptions/dependencies: Reliable structural parsers; domain-specific ontologies; validation datasets.
- Industry standards for “complexity stress testing” and disclosures
- Sectors: standards bodies, regulators, AI assurance.
- What: Require vendors to disclose performance vs. depth/branching; certify safe operating envelopes; mandate guardrails for long-tail complexity.
- Tools/products: Standardized stress-test suites; reporting templates; certification programs.
- Assumptions/dependencies: Multi-stakeholder consensus; alignment with regulatory frameworks.
- Next-generation KG QA stacks with dynamic planning
- Sectors: enterprise search, biomedical informatics.
- What: Hybrid stacks that decompose NL queries, invoke planner/search over KGs, and surface verifiable paths; adaptive re-querying when branch factor explodes.
- Tools/products: NL→KG planner compilers; interactive decomposition UIs; user-traceable justifications.
- Assumptions/dependencies: High-quality KGs; robust entity/relation grounding; user experience design for verifiability.
- Scalable proof planning assistants
- Sectors: formal methods, education, law.
- What: Systems that maintain global proof DAGs, prune branches efficiently, and interleave LLM suggestions with formal proof search; depth-adaptive curricula for learners.
- Tools/products: Lean/Coq co-pilots with planner backends; proof-difficulty classifiers; curriculum generators from DeepRD-like engines.
- Assumptions/dependencies: Improved search heuristics; low-latency proof checking; datasets with clean annotations.
- Autonomously-assisted scientific research agents
- Sectors: R&D across STEM, pharma, materials.
- What: Mixed-initiative agents that leverage graph-of-knowledge traversal, formal hypothesis testing, and tool-verified derivations; reserve LRMs for local reasoning and language mediation.
- Tools/products: Research planners; experiment simulators tied to verifiers; provenance and reproducibility logs.
- Assumptions/dependencies: Integration with domain tools (CAS, simulators, ELNs); robust verification; data access/governance.
- Hardware and runtime co-design for search + LLMs
- Sectors: semiconductor, cloud providers.
- What: Accelerators and runtimes that co-schedule neural inference with symbolic search/verifiers, minimizing overhead for deep reasoning.
- Tools/products: Unified execution frameworks; memory models optimized for graph expansion and caching.
- Assumptions/dependencies: Hardware-software co-design; workload characterization for search-heavy pipelines.
- Provenance and compliance infrastructure for reasoning
- Sectors: finance, healthcare, public sector.
- What: Proof-of-correctness and path provenance embedded in outputs; audit-ready records that include verified traversals and error bounds tied to complexity.
- Tools/products: Verifiable reasoning ledgers; red-team simulators that probe long-tail complexity.
- Assumptions/dependencies: Standards for explainability artifacts; secure storage; acceptance by regulators.
- Depth-adaptive tutoring and assessment
- Sectors: education technology.
- What: Tutors that adapt exercise depth/branching to student proficiency; explicitly teach failure modes (omissions, hallucinated links) and corrective strategies.
- Tools/products: Complexity-calibrated item banks; analytics on student vs. model complexity curves.
- Assumptions/dependencies: Content authoring aligned to DAG structures; measurement validity.
Cross-cutting assumptions and dependencies
- Complexity estimation is imperfect for unstructured NL; practical systems will use proxies (retrieval graph diameter, dependency distance, branching in candidate steps) and calibrate thresholds empirically.
- Graph encoding and prompt formats affect performance; standardized encodings reduce variance.
- Availability of graph databases, formal verifiers, and programmatic solvers is critical to realize hybrid workflows.
- Token limits are not the main bottleneck per the paper; generalization beyond training complexity is the core limitation—solutions must incorporate explicit search/verification.
- Real-world graphs often sit within the “head” of the distribution where LRMs work, but long-tail queries must be anticipated and safely handled by routing and verification.
Glossary
- Chain graph: A linear graph where each node has exactly one successor, forming a single path without branching. "Consider a chain graph (a graph of nodes connected one after the other)"
- Chain‑of‑thought (CoT): A prompting technique that elicits step‑by‑step reasoning from LLMs to improve accuracy and reduce hallucinations. "chainâofâthought"
- Clever Hans cheat: A shortcut strategy where a model exploits superficial cues (like single-child nodes) to answer without genuine search or reasoning. "termed the ``Clever Hans cheat'' in \citealt{DBLP:conf/icml/BachmannN24}"
- ConceptNet: A large, multilingual commonsense knowledge graph used for reasoning and knowledge tasks. "We also include ConceptNet"
- Deep Reasoning Dataset (DeepRD): A synthetic, parameterized benchmark that scales reasoning complexity for graph connectivity and natural‑language proof planning. "Deep Reasoning Dataset (DeepRD)"
- Directed acyclic graph (DAG): A directed graph with no cycles, often used to represent dependencies in proofs or computations. "directed acyclic graphs (DAGs)"
- Erdős–Rényi distribution: A random graph model where each edge is independently present with a fixed probability, used to generate benchmark graphs. "Erd\H{o}s--R " enyi distribution"
- Euler–Mascheroni constant: A mathematical constant (γ ≈ 0.57721) appearing in analytic number theory and graph path length estimates. "the Euler-Mascheroni constant"
- Graph coloring: The computational problem of assigning colors to vertices so adjacent ones differ, often used to test algorithmic reasoning. "graph coloring"
- Hamiltonian path: A path that visits each vertex exactly once; finding such paths is a classic combinatorial search problem. "finding Hamiltonian paths"
- Lean: A formal proof assistant and language used to write and verify mathematical proofs. "in Lean or unstructured natural language"
- LogicTree: An inference‑time method for structured proof exploration that uses caching and linearized premise selection. "LogicTree"
- Lookahead (L): A complexity metric defined as the number of BFS iterations needed to determine the next correct node toward a goal. "lookahead metric "
- MA‑LoT: A multi‑agent framework that separates natural‑language planning from formal verification in proof reasoning. "MAâLoT"
- Multi‑hop question‑answering: QA tasks requiring reasoning over multiple linked facts or entities through several steps. "multi-hop question-answering"
- Multi‑hop search: A search strategy that explores paths across multiple intermediary nodes to reach a target. "multi-hop search"
- NaturalProofs: A corpus of formal and natural‑language proofs used to evaluate proof verification and reasoning. "NaturalProofs"
- NaturalProver: A grounded proof generator that improves short proofs via retrieval and constrained decoding. "NaturalProver"
- NetworkX faster_could_be_isomorphic: A heuristic function that quickly filters graph pairs that could be isomorphic, reducing expensive checks. "faster_could_be_isomorphic"
- NLGraph: A benchmark that encodes graphs as natural‑language edge lists to test LLMs on graph reasoning tasks. "NLGraph"
- OGB (Open Graph Benchmark): A suite of large‑scale graph datasets (e.g., citation, knowledge, biomedical) for standardized evaluation. "Open Graph Benchmark (OGB;"
- ogbl‑wikikg2: A large Open Graph Benchmark knowledge graph dataset focused on Wikidata relations. "ogbl-wikikg2"
- ogbn‑papers100M: A massive OGB citation network dataset with 100M paper nodes used for graph learning tasks. "ogbn-papers100M"
- Out‑degree: The number of outgoing edges from a node, used as a measure of branching complexity. "(i.e., out-degree)"
- Out‑of‑distribution generalization: The ability of models to perform reliably on examples whose complexity or structure differs from their training data. "out-of-distribution generalization"
- Proof planning: The process of selecting and sequencing inference steps to construct a valid proof. "proof planning"
- Propagation error: A failure mode where an early local mistake causes later steps to be consistent but wrong, degrading end‑to‑end correctness. "``propagation error''"
- Reinforcement learning with verifiable rewards (RLVR): A training paradigm where models receive rewards for producing outputs that can be checked for correctness. "reinforcement learning with verifiable rewards (RLVR)"
- Selection‑inference framework: A method that separates premise selection from inference to improve reasoning reliability. "selectionâinference framework"
- Self‑consistency (SC): A technique that samples multiple reasoning chains and selects the most consistent answer to improve accuracy. "selfâconsistency"
- Self‑verification: A reasoning strategy where the model checks and validates its own intermediate deductions. "selfâverification"
- Thinking tokens: Special tokens (in some LRMs) that reveal intermediate reasoning steps used before producing the final answer. "thinking tokens"
- Wikidata5M: A large knowledge graph subset of Wikidata with millions of entities and facts used for multi‑hop reasoning. "Wikidata5M"
- Number of branches (B): The count of outgoing options from the start node; higher B increases ambiguity and guessing difficulty. "number of branches "
Collections
Sign up for free to add this paper to one or more collections.