DeepSeekMath-V2: Towards Self-Verifiable Mathematical Reasoning (2511.22570v1)
Abstract: LLMs have made significant progress in mathematical reasoning, which serves as an important testbed for AI and could impact scientific research if further advanced. By scaling reasoning with reinforcement learning that rewards correct final answers, LLMs have improved from poor performance to saturating quantitative reasoning competitions like AIME and HMMT in one year. However, this approach faces fundamental limitations. Pursuing higher final answer accuracy doesn't address a key issue: correct answers don't guarantee correct reasoning. Moreover, many mathematical tasks like theorem proving require rigorous step-by-step derivation rather than numerical answers, making final answer rewards inapplicable. To push the limits of deep reasoning, we believe it is necessary to verify the comprehensiveness and rigor of mathematical reasoning. Self-verification is particularly important for scaling test-time compute, especially for open problems without known solutions. Towards self-verifiable mathematical reasoning, we investigate how to train an accurate and faithful LLM-based verifier for theorem proving. We then train a proof generator using the verifier as the reward model, and incentivize the generator to identify and resolve as many issues as possible in their own proofs before finalizing them. To maintain the generation-verification gap as the generator becomes stronger, we propose to scale verification compute to automatically label new hard-to-verify proofs, creating training data to further improve the verifier. Our resulting model, DeepSeekMath-V2, demonstrates strong theorem-proving capabilities, achieving gold-level scores on IMO 2025 and CMO 2024 and a near-perfect 118/120 on Putnam 2024 with scaled test-time compute.
Sponsor
Summary
- The paper introduces a novel verifier-guided generation pipeline that shifts from final-answer rewards to detailed, stepwise proof evaluation.
- It integrates meta-verification to ensure reported errors and scores align with expert judgments, boosting analysis quality from 0.85 to 0.96.
- The architecture demonstrates superhuman results on IMO, CMO, and Putnam benchmarks, paving the way for autonomous, research-grade theorem proving.
DeepSeekMath-V2: Advancing Self-Verifiable Mathematical Reasoning
Motivation and Limitations of Final-Answer-Based Reward
Traditionally, reinforcement learning for mathematical reasoning with LLMs relies on rewarding models based solely on the correctness of final answers in quantitative competitions. This paradigm has yielded rapid progress, with models saturating major benchmarks such as AIME and HMMT. However, final-answer-centric evaluation fundamentally misrepresents reasoning correctness: a model can arrive at the right answer through flawed steps, and the metric itself is inapplicable to theorem-proving tasks where rigorous, stepwise derivation holds primacy over a mere solution.
Models trained in this regime reliably produce proofs that lack validity and rigor, exhibiting high false-positive rates when verifying their own or external proofs. The generation-verification gap remains unaddressed, with models often recognizing their outputs as valid when a mathematical expert would not.
Architecture: Verifier-Guided Generation and Meta-Verification
DeepSeekMath-V2 introduces a principled framework for self-verifiable mathematical reasoning with LLMs. The system employs an LLM-based verifier, trained to robustly identify and summarize defects in candidate proofs and assign scores based on rigor and completeness. Proof generators are then optimized using the verifier’s reward signal—transitioning away from final-answer reward to detailed scrutiny of reasoning steps.
A critical advance is the incorporation of meta-verification. The meta-verifier is trained to evaluate not only proofs but also the verifier’s analyses: it ensures that reported issues in a proof are real and that scores are justified per high-level rubrics. Incorporating this second-order feedback in the training loop reduces hallucinated errors and aligns verification outputs with expert mathematical judgment, producing consistent verification outcomes with a substantial increase in analysis quality (from 0.85 to 0.96 on held-out data).
Additionally, the generator is explicitly prompted to produce self-analyses of its own solutions, learning to accurately score and diagnose its outputs. A composite reward function combines rigorous proof synthesis and self-evaluation fidelity, incentivizing the generator to recognize and fix issues before considering a proof final.
Automated Data Curation and Scaling Compute
DeepSeekMath-V2 employs an iterative cycle: the generator improves by resolving shortcomings surfaced by verifier scrutiny; the verifier, originally initialized via manually curated datasets from AoPS contest problems, is re-trained on challenging instances surfaced as models improve. To scale training to IMO-level hardness and beyond, the pipeline fully automates labeling. For each proof, multiple independent verifier and meta-verifier assessments are sampled, issues are majority-validated, and only proofs confidently labeled are retained for further optimization—bypassing expensive manual annotation without loss in alignment to expert judgments.
Sequential refinement via self-verification and search—where candidate proofs are iteratively improved in response to identified flaws—demonstrates significant increases in both pass@1 and best@k verification scores across high-difficulty benchmarks.
Empirical Results and Benchmarking
Theorem Proving Performance
DeepSeekMath-V2 exhibits consistent superhuman performance across established theorem-proving suites and international competitions. On an internally curated set of 91 CNML-level problems spanning algebra, geometry, number theory, combinatorics, and inequality, the model achieves clear gains over GPT-5-Thinking-High and Gemini 2.5-Pro.
Figure 1: Average proof scores on CNML-level problems by category and model, as evaluated by our verifier.
For high-stakes benchmarks:
- IMO 2025: Solves 5 out of 6 problems outright, achieving gold-level scores.
- CMO 2024: Solves 4, with partial credit on a fifth, again attaining gold-medal status.
- Putnam 2024: Achieves 118/120, surpassing the top human score (90).
Notably, on the IMO-ProofBench, DeepSeekMath-V2 outperforms DeepThink (IMO Gold) and all prior systems on the Basic subset, and remains competitive at the Advanced level.
Figure 2: Expert evaluation results on the Basic and Advanced subsets of IMO-ProofBench. All results are sourced from \cite{imobench}.
The model demonstrates robust capacity for recognizing its own errors via self-verification and systematically refining proofs, with scaled compute yielding further improvements in rigor and coverage at test time. For unsolved cases, it generally identifies genuine issues—an essential precursor for automated mathematical research.
Theoretical and Practical Implications
The research establishes that self-verification through LLM-based verifiers and meta-verifiers substantially closes the reasoning correctness gap historically present in open-ended mathematical tasks. This framework for automated, scalable proof verification and generation enables the development of models capable of research-grade mathematical reasoning—with high-confidence proof production, rigorous error diagnosis, and the ability to improve by iterative self-aware judgment.
Practically, these capabilities will accelerate mathematical discovery, assist in formal theorem proving pipelines (with systems such as Lean and Isabelle), and facilitate downstream advancements in AI-driven science. The synergy of informal, natural-language reasoning with formal verification opens pathways for hybrid systems achieving state-of-the-art performance in proof synthesis and validation.
Ongoing work is warranted to address lingering limitations, especially in scaling to open problems and extending reliability in domains with highly entangled, multi-step logical structures.
Conclusion
DeepSeekMath-V2 delivers a comprehensive architecture for self-verifiable mathematical reasoning by integrating stringent LLM-based proof verification, meta-verification for analysis alignment, generator self-assessment, and scalable data automation. Empirical results verify strong gains over existing systems on competitive mathematical tasks. These advances suggest self-verifiable AI systems are technically feasible, setting foundations for autonomous agents capable of reliable, generalizable research-level theorem proving and mathematical discovery.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview: What this paper is about
This paper introduces DeepSeekMath-V2, an AI system that can both write math proofs and check whether those proofs are truly correct. Instead of only aiming for the right final answer (like “42”), it focuses on making sure every step of the reasoning is solid. The big idea is “self-verifiable reasoning”: the AI learns to spot problems in its own work and fix them before saying “I’m done.”
Key goals and questions
The authors wanted to solve three main problems:
- Final answers aren’t enough. A correct number can come from wrong steps. How can we judge the quality of the reasoning itself?
- Many math tasks (like theorem proving) don’t have a final number. How can an AI handle “show your work” problems?
- How can we build an AI that not only generates proofs but also reliably checks them, even when there’s no official solution to compare against?
In simple terms: Can we train an AI to be both a good problem solver and a trustworthy teacher-grader of proofs?
How they did it (methods in plain language)
Think of the system as three parts: a proof maker, a proof checker, and a checker of the checker.
- A proof checker (the Verifier)
- What it does: Given a math problem and a proof, it looks for issues and gives a score:
- 1 = fully correct and rigorous
- 0.5 = mostly right but with minor gaps
- 0 = seriously flawed
- How it learned: The team collected real contest problems and AI-written proofs, then had math experts score them. The verifier was trained to match expert judgments and to write clear explanations of what’s wrong or right.
- Why this matters: It’s like training a careful math teacher who can grade proofs and explain the grade.
- A checker of the checker (the Meta-Verifier)
- Problem: A checker could “hallucinate” issues — claiming mistakes that aren’t there — yet still guess the right final score.
- Solution: Train a second model to judge the first checker’s analysis. It asks: “Do the claimed issues actually exist? Do they justify the score?”
- Why this matters: It keeps the verifier honest and reduces made-up criticisms.
- A proof maker (the Generator) that learns to self-check
- What it does: Writes a proof, then writes a self-evaluation in the same format as the verifier.
- How it’s rewarded:
- It gets points for producing correct proofs (as judged by the verifier).
- It also gets points for being honest and accurate in its self-check (as judged by the meta-verifier).
- Why this matters: The model learns that admitting and fixing errors is better than pretending everything is perfect. It’s like a student who learns to grade their own work honestly and improve it before turning it in.
- The improvement loop (maker ↔ checker synergy)
- As the generator gets better, it creates new, harder-to-check proofs.
- The verifier then needs to level up, too.
- To do this efficiently, they “scale verification compute”: run many independent checks and meta-checks to automatically label whether a proof is good or not. If several checks agree there’s a real issue, that becomes a training label — without needing a human every time.
- Why this matters: This loop lets both the proof-maker and proof-checker keep improving together, even on hard problems.
- High-compute search (trying many ideas and refining)
- For the hardest problems, the system:
- Generates many different proof attempts.
- Runs many checks to find subtle mistakes.
- Iteratively refines the best candidates, guided by the verifier’s feedback.
- Think of it as exploring many possible solution paths in parallel, while a careful teacher points out where each path goes wrong.
Main findings and why they’re important
What the model achieved:
- Strong performance on real competitions:
- International Mathematical Olympiad (IMO 2025): solved 5 of 6 problems (gold-level performance).
- China Mathematical Olympiad (CMO 2024): solved most problems, plus partial credit on another (gold-level performance).
- Putnam 2024 (undergraduate level): scored 118/120, higher than the top human score reported.
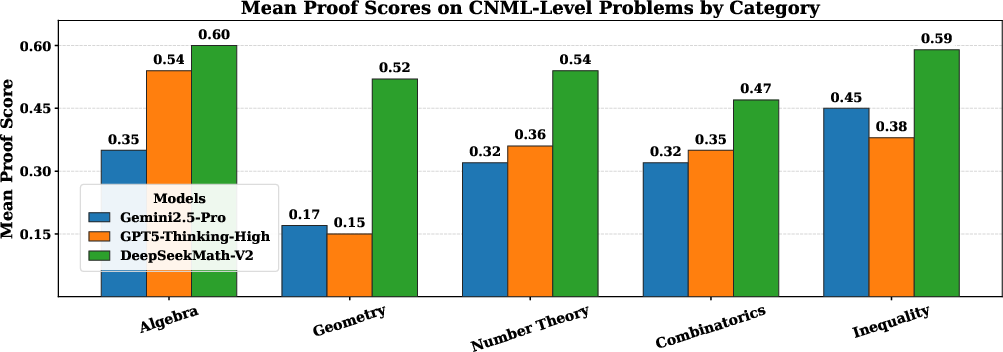
- On a range of theorem-proving benchmarks (across algebra, geometry, number theory, combinatorics, inequalities), it beat or matched leading AI systems.
- The model reliably improves its own proofs through self-verification and multiple rounds of refinement. It also gets better when given more “thinking time” and checking power.
Why this matters:
- It shows that AI can move beyond “final-answer guessing” to careful, step-by-step reasoning.
- It provides evidence that AI can judge proofs without needing an official solution — crucial for research problems where no answers exist yet.
- The “checker of the checker” reduces false alarms and builds trust in the AI’s assessments.
What this could mean for the future
- Better tools for learning and teaching: Imagine a math helper that not only solves problems but explains which steps are shaky and how to fix them.
- Help with open research problems: Since the system can verify reasoning without known answers, it may assist mathematicians in exploring new ideas more safely.
- Foundations for reliable scientific AI: This “self-verifiable reasoning” approach could guide AI in other fields that require careful logic and evidence, not just quick answers.
- Bridges to formal proof systems: Strong informal reasoning and checking can feed into formal proof tools (which guarantee correctness), speeding up rigorous mathematics.
In short: This work suggests a path to AI that doesn’t just get answers — it understands, checks, and improves its own reasoning, making it a more trustworthy partner for serious mathematics.
Knowledge Gaps
Below is a single, consolidated list of knowledge gaps, limitations, and open questions that remain unresolved in the paper. Each item is framed to enable concrete follow-up by future researchers.
- Quantify verifier reliability end-to-end: establish false-positive/false-negative rates of the verifier and meta-verifier across domains and difficulty levels, using independent expert panels or formal proof checkers instead of the model’s own meta-verifier.
- Avoid circular evaluation: many reported improvements (e.g., 0.85→0.96 analysis quality) are judged by the meta-verifier; design evaluations where neither the verifier nor meta-verifier participates (e.g., blinded external graders, formal systems).
- Step-level faithfulness: move beyond coarse overall scores {0, 0.5, 1} to fine-grained, step-by-step validation and error attribution; measure whether each inference is justified and track error propagation.
- Adversarial robustness: test whether generators can craft persuasive but incorrect proofs that systematically fool the verifier/meta-verifier; build adversarial test suites and red-teaming protocols.
- Generalization beyond competition-style math: evaluate on research-level proofs, multi-lemma arguments, probabilistic existence proofs, and areas requiring richer objects (e.g., measure theory, topology) to assess scope and limits.
- Geometry and diagrammatic reasoning: explicitly paper verification for geometry proofs that depend on constructions, diagrams, and non-textual constraints; integrate symbolic/diagram checks.
- Formal–informal alignment: quantify how often “verified” informal proofs can be converted to fully formal proofs in Lean/Isabelle and where the pipeline fails; create a mapping of failure causes.
- Data contamination controls: release decontamination procedures and evidence that IMO/CMO/Putnam/ISL test sets were not seen during pretraining/fine-tuning; provide dataset hashes and audit trails.
- Automated labeling calibration: the pipeline’s parameters (, , , “lowest score” rule) and majority-vote thresholds are unquantified; derive statistical confidence bounds and target error rates as functions of these parameters.
- Confidence estimation: passing 64 verification attempts is treated as “high confidence” without probabilistic calibration; provide well-calibrated confidence intervals and error guarantees under repeated verification.
- Sensitivity analyses: justify the reward weights (e.g., α=0.76, β=0.24), format rewards, and rubric choices via ablations; report how performance changes when these are perturbed.
- Compute–accuracy scaling laws: characterize how verification/generation performance scales with compute (threads, iterations, context length), and identify diminishing returns and optimal budget allocation strategies.
- Fairness of model comparisons: standardize prompts, sampling budgets, context limits, and verification budgets across baselines (GPT-5-Thinking-High, Gemini 2.5-Pro) to ensure apples-to-apples comparisons; publish configs and seeds.
- Inter-annotator agreement: when human experts are used, report agreement statistics, adjudication protocols, and grading rubrics; release representative annotated samples.
- Error taxonomy: provide a systematic breakdown of common failure modes (logical gaps, invalid lemmas, unjustified leaps, definition misuse, hidden case splits), stratified by domain (algebra, geometry, NT, combinatorics, inequalities).
- Cross-model verification: test whether heterogeneous verifiers (different base models/training) agree on proof validity; paper ensemble or cross-checking to reduce correlated errors.
- Aggregation robustness: majority-vote and “lowest score” aggregation may select spurious analyses; explore robust aggregation (e.g., Dawid–Skene, Bayesian truth inference) and adjudication of contradictory analyses.
- Counterexample search: integrate automated counterexample generation (symbolic, numeric) to detect flawed claims that textual verification misses, especially in inequalities and functional equations.
- Retrieval and long-context management: the 128K context limit constrains multi-iteration refinement; evaluate memory mechanisms, retrieval augmentation, or hierarchical proof state tracking across iterations/threads.
- Open-problem protocol: define safeguards for self-verification on unsolved problems to prevent false claims of resolution; require independent formalization or third-party expert review before asserting correctness.
- Provenance and theorem usage: verify that referenced lemmas/theorems are valid and appropriately invoked; build a vetted knowledge base and citation checking within the verifier.
- Robustness to format gaming: the format reward (key phrases, boxed scores) may incentivize superficial compliance; design format-agnostic scoring extraction and penalize templated but unsubstantiated evaluations.
- Transfer to other domains: test the self-verification framework in proofs outside mathematics (algorithms, logic, physics derivations) and identify necessary domain adaptations.
- Training cost transparency: report RL hyperparameters, total tokens/updates, wall-clock compute, and energy consumption; analyze efficiency vs. accuracy trade-offs and pathways to resource-constrained deployment.
- Release and reproducibility: clarify which models, code, prompts, datasets, and labels are publicly available; provide instructions to reproduce the automated labeling pipeline and evaluation results.
- Maintaining the generation–verification gap: formalize what “gap” means and track it quantitatively across training iterations; paper mechanisms to prevent generator–verifier collusion or convergence to shared biases.
- Partial-credit modeling: replace coarse {0, 0.5, 1} scores with richer rubrics aligned to competition grading schemes (point-based with criterion-level checks); evaluate effects on training and downstream scoring fidelity.
- Domain shift monitoring: AoPS-derived training may bias the verifier towards Olympiad-style reasoning; measure performance under distribution shift (textbook proofs, research papers, formal seminar notes).
- Meta-verifier learning dynamics: investigate whether meta-verification is truly easier/more sample-efficient; supply learning curves, sample complexity analyses, and transfer properties across tasks.
- Hardest-problem analysis: for IMO-hard items not fully solved, provide case studies showing exactly why verification/generation failed and what additional capabilities would be required.
Glossary
- AIME: The American Invitational Mathematics Examination, a U.S. high-school mathematics contest often used as a benchmark. "saturate mathematical competitions that primarily evaluate final answers, such as AIME and HMMT."
- AlphaProof: A DeepMind system specialized in formal proof search for mathematical problems. "AlphaProof \citep{alphaproof,alphageometry,alphageometry2}, a system specialized for formal proof search, achieved silver-level performance at IMO 2024 but required intensive computation."
- AoPS (Art of Problem Solving): An online community and resource hub for math competitions and problem solving. "We crawled problems from Art of Problem Solving (AoPS) contests \footnote{\url{https://artofproblemsolving.com/community/c13_contest_collections}, prioritizing math olympiads, team selection tests, and post-2010 problems explicitly requiring proofs, totaling 17,503 problems."
- Best@32: A selection metric indicating the best result among 32 independent attempts based on self-assigned scores. "We report two metrics in Figure~\ref{fig:seq_refine}: (1) Pass@1 -- the average score of the final proof from each thread, and (2) Best@32 -- the score of the best proof per problem, selected by self-assigned scores across all threads."
- CMO (China Mathematical Olympiad): China’s national high-school mathematics competition. "CMO 2024 (6 problems): The China Mathematical Olympiad, China's national championship"
- CNML (Chinese National High School Mathematics League): A Chinese national-level high-school mathematics league used as a difficulty benchmark. "comparable in difficulty to problems from Chinese National High School Mathematics League (CNML)"
- DeepSeek-Prover-V2: A system advancing formal mathematical reasoning via reinforcement learning for subgoal decomposition. "Systems like DeepSeek-Prover-V2 \citep{deepseekproverv2} and Seed-Prover \citep{seedprover} can now produce substantially more valid formal proofs within the same computational budget, with Seed-Prover solving 5 of 6 problems at IMO 2025."
- DeepSeekMath-V2: The paper’s LLM optimized for natural-language theorem proving with self-verification. "Built on DeepSeek-V3.2-Exp-Base \citep{deepseekv32}, we developed DeepSeekMath-V2, a LLM optimized for natural-language theorem proving that demonstrates self-verifiable mathematical reasoning."
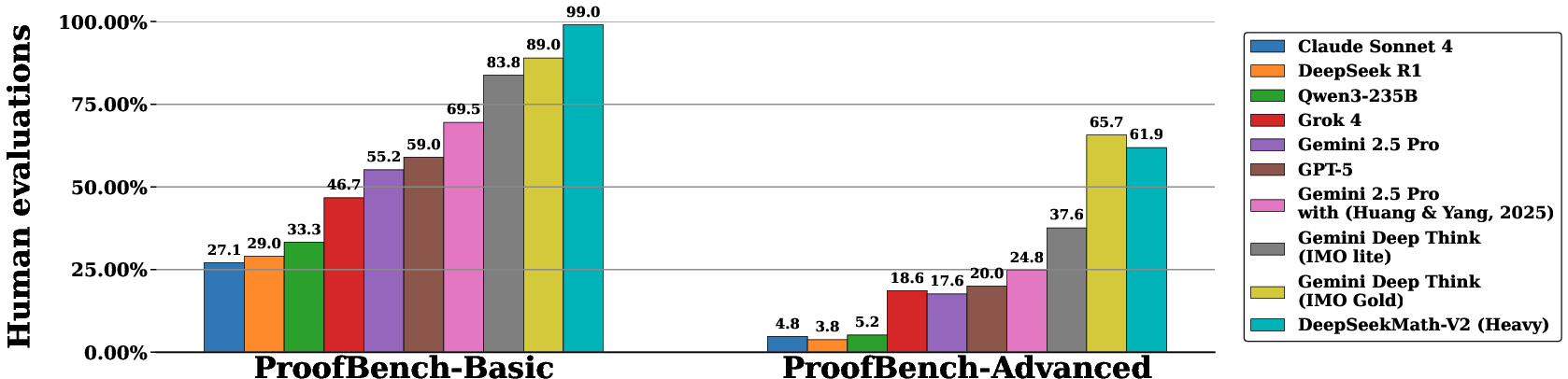
- DeepThink (IMO Gold): An internal DeepMind variant achieving gold-medal performance on IMO-level problems. "Developed by the DeepMind team behind DeepThink IMO-Gold \citep{deepthinkimo}, this benchmark \citep{imobench} is divided into a basic set (30 problems, pre-IMO to IMO-Medium difficulty) and an advanced set (30 challenging problems simulating complete IMO examinations, up to IMO-Hard level)"
- Gemini 2.5 Pro: A Google DeepMind LLM used as a baseline. "DeepSeekMath-V2 consistently outperforms GPT-5-Thinking-High \citep{gpt5} and Gemini 2.5-Pro \citep{gemini}, demonstrating superior theorem-proving ability across domains."
- Generative reward model: A model that provides reward signals for reinforcement learning to guide generation (here, a verifier scoring proofs). "With verifier $\pi_$ serving as a generative reward model, we train a proof generator with the RL objective:"
- Generation-verification gap: The discrepancy between a model’s ability to generate solutions and its ability to rigorously verify them. "The lack of a generation-verification gap in natural-language theorem proving hinders further improvement."
- GRPO (Group Relative Policy Optimization): A reinforcement learning algorithm for optimizing policies using grouped relative performance. "We employed Group Relative Policy Optimization (GRPO) \citep{deepseekmath} for reinforcement learning, iteratively optimizing proof verification and generation capabilities as described in Section~\ref{sec:method}."
- HMMT (Harvard–MIT Mathematics Tournament): A prestigious high-school mathematics competition used as a benchmark. "saturate mathematical competitions that primarily evaluate final answers, such as AIME and HMMT."
- IMO (International Mathematical Olympiad): The premier global mathematics competition for pre-university students. "IMO 2025 (6 problems): The International Mathematical Olympiad, the premier global mathematics competition for pre-university students"
- IMO-ProofBench: A benchmark of IMO-style problems designed to assess proof quality and robustness. "IMO-ProofBench (60 problems): Developed by the DeepMind team behind DeepThink IMO-Gold \citep{deepthinkimo}, this benchmark \citep{imobench} is divided into a basic set (30 problems, pre-IMO to IMO-Medium difficulty) and an advanced set (30 challenging problems simulating complete IMO examinations, up to IMO-Hard level)"
- ISL (IMO Shortlist): The collection of problems proposed by countries and considered for inclusion in the IMO. "ISL 2024 (31 problems): The IMO Shortlist, a collection of problems proposed by participating countries and considered by the Problem Selection Committee for potential inclusion in IMO 2024"
- Isabelle: A formal proof assistant used to verify proofs by compiling them into a formal language. "Proof assistants like Lean \citep{lean} and Isabelle \citep{isabelle} offer a reliable approach to verify proofs -- proofs must be written in formal language, but once compiled, correctness is guaranteed."
- LLM: A machine learning model trained to process and generate human language at scale. "LLMs have improved from poor performance to saturating quantitative reasoning competitions like AIME and HMMT in one year."
- Lean: A formal proof assistant for writing and checking mathematical proofs. "Proof assistants like Lean \citep{lean} and Isabelle \citep{isabelle} offer a reliable approach to verify proofs -- proofs must be written in formal language, but once compiled, correctness is guaranteed."
- Majority voting: An aggregation method that decides correctness based on the majority of verification outputs. "Proof correctness was measured by majority voting across 8 verification analyses produced by our final verifier."
- Meta-verification: A second-order evaluation that checks whether identified issues by the verifier are real and justify the score. "To address this problem, we introduce meta-verification: a secondary evaluation process that assesses whether issues identified by the verifier indeed exist and whether these issues logically justify the predicted proof score according to the evaluation rubrics ."
- Meta-verifier: A model trained to evaluate the verifier’s analysis for accuracy and justification. "We trained a dedicated meta-verifier using RL to perform this evaluation."
- Pass@1: A metric capturing the average score of the final proof from a single attempt per refinement thread. "We report two metrics in Figure~\ref{fig:seq_refine}: (1) Pass@1 -- the average score of the final proof from each thread, and (2) Best@32 -- the score of the best proof per problem, selected by self-assigned scores across all threads."
- Proof assistant: Software that checks the correctness of formal proofs written in a specific language. "Proof assistants like Lean \citep{lean} and Isabelle \citep{isabelle} offer a reliable approach to verify proofs -- proofs must be written in formal language, but once compiled, correctness is guaranteed."
- Proof generator: A model that produces candidate proofs for mathematical problems. "With verifier $\pi_$ serving as a generative reward model, we train a proof generator with the RL objective:"
- Proof verifier: A model that analyzes proofs, identifies issues, and assigns scores according to rubrics. "We then train a proof generator using the verifier as the reward model, and incentivize the generator to identify and resolve as many issues as possible in their own proofs before finalizing them."
- Putnam (William Lowell Putnam Competition): The leading undergraduate mathematics competition in North America. "Putnam 2024 (12 problems): The William Lowell Putnam Competition, the preeminent mathematics competition for undergraduate students in North America"
- Rejection fine-tuning: A training technique that consolidates capabilities by preferentially fine-tuning on accepted outputs after rejecting inferior ones. "Starting from the second iteration, the proof verifier was initialized with a checkpoint that consolidated both verification and generation capabilities from the previous iteration through rejection fine-tuning."
- Reinforcement learning (RL): A training paradigm where models learn by maximizing reward signals based on performance. "The conventional approach to reinforcement learning (RL) for mathematical reasoning involves rewarding LLMs based on whether their predicted final answers to quantitative reasoning problems match ground-truth answers \citep{deepseek-r1}."
- Reward model: A model that provides scalar rewards to guide another model’s learning process. "We then train a proof generator using the verifier as the reward model, and incentivize the generator to identify and resolve as many issues as possible in their own proofs before finalizing them."
- Seed-Prover: A system that generates valid formal proofs efficiently, achieving high performance on IMO problems. "Systems like DeepSeek-Prover-V2 \citep{deepseekproverv2} and Seed-Prover \citep{seedprover} can now produce substantially more valid formal proofs within the same computational budget, with Seed-Prover solving 5 of 6 problems at IMO 2025."
- Self-verification: A model’s ability to evaluate and improve its own proofs by identifying and addressing issues. "Self-verification is particularly important for scaling test-time compute, especially for open problems without known solutions."
- Test-time compute: The amount of computational resources allocated during inference, often scaled to improve solution quality. "Self-verification is particularly important for scaling test-time compute, especially for open problems without known solutions."
- Theorem proving: The task of producing rigorous, step-by-step proofs of mathematical statements. "we investigate how to train an accurate and faithful LLM-based verifier for theorem proving."
- Verification analyses: Multiple independent evaluations of a proof produced by the verifier. "Proof correctness was measured by majority voting across 8 verification analyses produced by our final verifier."
- Verification compute: The computational budget devoted to verifying proofs, which can be scaled to improve reliability. "we propose to scale verification compute to automatically label new hard-to-verify proofs, creating training data to further improve the verifier."
Practical Applications
Immediate Applications
Below are actionable use cases that can be deployed now, leveraging the paper’s verifier, meta-verifier, self-verification training, sequential refinement, and automated labeling pipeline.
- Industry (Software/DevTools): CI-integrated “Verified Reasoning Mode” for algorithm docs and technical design reviews
- What: Developers attach proof-like rationales (invariants, complexity arguments, safety claims) to PRs; the pipeline runs multi-sample verification and meta-verification to produce a score plus a concrete issue list before merge.
- Tools/Workflow: Verifier-as-a-Service API; auto-gating by majority-vote verification; standardized rubric prompts; issue summaries exported into PR comments.
- Assumptions/Dependencies: Domain-specific rubrics beyond olympiad math; long-context inference; budget for parallel verification (e.g., 8–64 analyses); human override for edge cases.
- Industry (Finance/Risk): Quant model validation assistant for pricing, hedging, and risk memos
- What: Checks derivations and consistency in model documentation; flags gaps and assigns confidence scores for audit trails.
- Tools/Workflow: Batch verification on internal model notes; meta-verification to vet identified issues; dashboard with “verification confidence” and issue taxonomy.
- Assumptions/Dependencies: Secure on-prem deployment; adaptation to finance math (stochastic calculus, numerical schemes); careful handling of proprietary data; human quant sign-off.
- Industry (Engineering/Energy/Robotics): Safety-case reasoning QA for constraint proofs and formal claims in design documents
- What: Verifies the logical soundness of safety claims, stability proofs, and constraint satisfaction arguments in engineering artifacts.
- Tools/Workflow: Sequential refinement to resolve flagged issues; verification logs appended to certification packages.
- Assumptions/Dependencies: Strong domain rubrics; clear linkage between informal proofs and formal requirements; human-in-the-loop for sign-off.
- Industry (ML Ops): Automated labeler for reasoning datasets
- What: Uses scaled verification + meta-verification (n/m/k majority gating) to auto-score synthetic proofs and reduce manual annotation.
- Tools/Workflow: Orchestrated candidate sampling (e.g., 64 analyses); quality checks; routing uncertain cases to experts; dataset versioning.
- Assumptions/Dependencies: Compute budget; careful selection of n, m, k; monitoring for label drift and false negatives.
- Academia (Education): Auto-grading and formative feedback for proof-based assignments
- What: Scores student proofs, gives constructive issue summaries, and supports partial credit aligned with course rubrics.
- Tools/Workflow: LMS plug-in; instructor-defined rubrics; iterative refinement suggestions; gradebook integration.
- Assumptions/Dependencies: Rubric customization; safeguards against bias and grading errors; instructor review of borderline cases.
- Academia (Mathematics Research): Proof polishing and triage assistant
- What: Helps authors detect gaps in natural-language proofs, iterate with self-verification, and elevate proof quality prior to submission.
- Tools/Workflow: Sequential refinement within a notebook/IDE; “pass-all-verifications” threshold as a confidence indicator; exportable verification reports.
- Assumptions/Dependencies: High compute for difficult proofs; remains a heuristic (not a formal guarantee); domain-specific tuning for subfields.
- Academia (Bridging to Formal Methods): Subgoal decomposition for formalization (Lean/Isabelle)
- What: Use self-verified natural-language proofs to propose formal subgoals and structure for downstream formal proof assistants.
- Tools/Workflow: Verifier-guided outline → subgoal tree → formalization scripts/templates; integration with existing provers.
- Assumptions/Dependencies: Mappings from informal steps to formal tactics; coverage of domain libraries; human oversight for formal correctness.
- Publishing/Peer Review: Meta-reviewer triage for proof-heavy papers
- What: Flags missing steps and unsubstantiated leaps in submitted proofs; helps editors direct reviewers to critical sections.
- Tools/Workflow: Batch verification; meta-verifier validates issue lists; report attached to submission package.
- Assumptions/Dependencies: Domain adaptation (e.g., algebraic geometry, combinatorics); editorial acceptance; confidentiality controls.
- Policy/Compliance: “Self-Verification Report” attachment for quant-heavy proposals and regulatory filings
- What: Requires a standardized verification log and issue list for high-stakes quantitative claims in public policy or compliance documents.
- Tools/Workflow: Template-based rubric evaluation; thresholding (e.g., must pass N verifications); archivable reports for auditing.
- Assumptions/Dependencies: Institutional buy-in; review guidelines; human adjudication for contested findings.
- Daily Life (Learning/Tutoring): Olympiad-level proof tutor and paper companion
- What: Guides learners with step-by-step feedback; encourages iteration until the proof passes verification.
- Tools/Workflow: Interactive prompt templates; sequential refinement loop; score-based progress tracking.
- Assumptions/Dependencies: Availability of long-context models; caution on edge cases; user education about limitations.
Long-Term Applications
These use cases are promising but require further research, domain adaptation, scaling, or productization beyond current capabilities.
- Cross-Domain Reasoning Verification (Healthcare, Physics, Economics, Law)
- What: Extend the self-verification paradigm to diverse disciplines (clinical evidence chains, physical derivations, economic models, legal argumentation).
- Tools/Workflow: Domain-specific rubrics; curated training corpora; multi-expert benchmarking; cross-modality inputs (figures, data tables).
- Assumptions/Dependencies: Significant rubric/ontology design; potential multimodal context; higher stakes require stringent human oversight.
- End-to-End Formalization of Advanced Proofs
- What: Automatically transform self-verified natural-language proofs into fully formal Lean/Isabelle proofs at scale.
- Tools/Workflow: Verifier-guided subgoal decomposition; tactic synthesis; counterexample search; tight feedback loops with proof assistants.
- Assumptions/Dependencies: Robust mapping from informal to formal semantics; expanded libraries; compute-intensive search; rigorous evaluation.
- Open-Problem Co-Research with Scaled Test-Time Compute
- What: Orchestrate parallel candidate pools and verifier-guided refinement to explore new proof strategies on research-level problems.
- Tools/Workflow: High-compute search (64+ candidates × iterations); confidence thresholds (pass-all-verifications); collaboration dashboards for human-AI teams.
- Assumptions/Dependencies: Substantial compute budgets; careful deduplication and novelty detection; human mathematician guidance.
- Verified Scientific Methods Checker across STEM Publishing
- What: Standardize “verification certificates” for methods sections, derivations, and statistical claims in journal submissions.
- Tools/Workflow: Journal-integrated pipelines; cross-field rubric libraries; meta-verification audits; provenance tracking.
- Assumptions/Dependencies: Community standards; legal/ethical frameworks; acceptance by publishers and funders.
- Safety Assurance in Autonomy (Robotics/Transportation/Energy)
- What: Require self-verification logs for control proofs (stability, reachability, safety envelopes) before deployment of autonomous systems.
- Tools/Workflow: Continuous verification on updated policies; fail-safe thresholds; integration with formal safety monitors.
- Assumptions/Dependencies: Bridging informal verification with certified formal components; regulator acceptance; incident response protocols.
- Regulatory Standards for “Self-Verifiable AI”
- What: Define minimum verification thresholds (e.g., number of independent analyses, meta-verification agreement rates) for AI systems used in high-stakes contexts.
- Tools/Workflow: Compliance dashboards; audit trails; standardized reporting schemas; independent third-party evaluators.
- Assumptions/Dependencies: Policy-making processes; sector-specific calibration; evolving best practices.
- Personalized, Curriculum-Scale Proof Learning Systems
- What: Adaptive learning platforms that scaffold from informal reasoning to formal proofs, guided by self-verification scores and issue taxonomies.
- Tools/Workflow: Longitudinal learner models; fine-grained rubrics; automated pathway generation; formative analytics.
- Assumptions/Dependencies: Data privacy; fairness; robust error remediation; sustained compute for large cohorts.
- General-Purpose “Reasoning Label Factory” for LLM Training
- What: Industrial-scale auto-labeling of reasoning datasets across domains using multi-sample verification and meta-verification to replace most human annotation.
- Tools/Workflow: Orchestration for n/m/k sampling; quality checks; continuous improvement via hard-case mining; cost-aware scheduling.
- Assumptions/Dependencies: Stable base models; guardrails against spurious consensus; adaptive thresholds to control precision/recall.
- Enterprise “Proof Ops” Platforms
- What: End-to-end infrastructure for managing proof generation, verification, meta-verification, sequential refinement, and high-compute search in mission-critical workflows.
- Tools/Workflow: Job schedulers; candidate pools; verifier scoreboards; human-in-the-loop gates; compliance logging.
- Assumptions/Dependencies: Organizational change management; cloud/on-prem hybrid deployment; robust SLAs; governance frameworks.
Cross-cutting assumptions and dependencies to monitor
- Domain transfer: Rubrics and verifier reliability must be adapted and validated for each sector; math-specific training will not generalize perfectly.
- Compute and latency: Many workflows rely on parallel verification (8–64+ analyses) and long-context inference; costs need careful management.
- Format and process fidelity: Consistent, enforceable output formats (score + issue summary) are essential for automation and gating.
- Human oversight: High-stakes decisions require human review and adjudication; use verification scores as triage, not ground truth.
- Robustness: Guard against correlated model errors and spurious majority consensus; maintain calibration and perform adversarial testing.
- Data governance: Protect proprietary or sensitive documents; ensure reproducible verification logs and auditability.
Collections
Sign up for free to add this paper to one or more collections.