Deep Self-Evolving Reasoning (2510.17498v1)

Abstract: Long-form chain-of-thought reasoning has become a cornerstone of advanced reasoning in LLMs. While recent verification-refinement frameworks have enabled proprietary models to solve Olympiad-level problems, their effectiveness hinges on strong, reliable verification and correction capabilities, which remain fragile in open-weight, smaller-scale models. This work demonstrates that even with weak verification and refinement capabilities on hard tasks, the reasoning limits of such models can be substantially extended through a probabilistic paradigm we call Deep Self-Evolving Reasoning (DSER). We conceptualize iterative reasoning as a Markov chain, where each step represents a stochastic transition in the solution space. The key insight is that convergence to a correct solution is guaranteed as long as the probability of improvement marginally exceeds that of degradation. By running multiple long-horizon, self-evolving processes in parallel, DSER amplifies these small positive tendencies, enabling the model to asymptotically approach correct answers. Empirically, we apply DSER to the DeepSeek-R1-0528-Qwen3-8B model. On the challenging AIME 2024-2025 benchmark, DSER solves 5 out of 9 previously unsolvable problems and boosts overall performance, enabling this compact model to surpass the single-turn accuracy of its 600B-parameter teacher through majority voting. Beyond its immediate utility for test-time scaling, the DSER framework serves to diagnose the fundamental limitations of current open-weight reasoners. By clearly delineating their shortcomings in self-verification, refinement, and stability, our findings establish a clear research agenda for developing next-generation models with powerful, intrinsic self-evolving capabilities.

• The paper introduces DSER, a probabilistic framework that guides open-weight LLMs toward correct solutions using iterative self-evolving reasoning.
• It reformulates the verification–refinement loop as a Markov chain, statistically biasing improvement and outperforming traditional methods on AIME benchmarks.
• Empirical evaluations show DSER enhances DS-8B’s Pass@1 accuracy and reliably solves hard math problems through majority voting over iterative refinements.

Deep Self-Evolving Reasoning: Extending the Reasoning Boundaries of Open-Weight LLMs

Introduction

The paper "Deep Self-Evolving Reasoning" (DSER) (2510.17498) presents a probabilistic framework for iterative reasoning in LLMs, specifically targeting open-weight, small- and medium-scale models with limited verification and refinement capabilities. The central thesis is that long-horizon, self-evolving reasoning—conceptualized as a Markov chain—can asymptotically guide models toward correct solutions, even when individual reasoning steps are unreliable. This paradigm is empirically validated on the DeepSeek-R1-0528-Qwen3-8B model, demonstrating substantial improvements on the AIME 2024-2025 mathematical competition benchmarks.

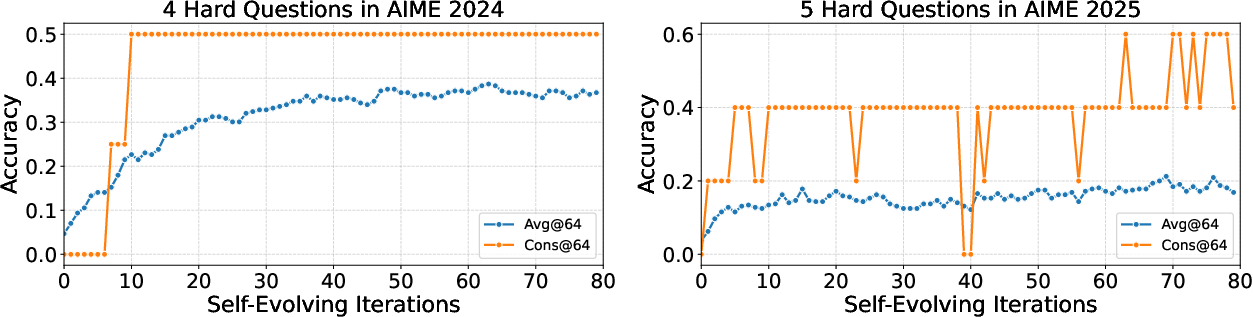
Figure 1: DSER enables DeepSeek-R1-0528-Qwen3-8B to solve 5 of 9 previously unsolvable AIME problems, with majority voting over the last ten self-evolving iterations yielding the correct answer.

Probabilistic Formulation of Iterative Reasoning

DSER reframes the classic verification–refinement loop as a stochastic process governed by a Markov chain. Each reasoning iteration is a transition in the solution space, with the transition matrix $P$ parameterized by the probabilities of improvement ($p_{IC}$: incorrect $\to$ correct) and degradation ($p_{CI}$: correct $\to$ incorrect). The stationary distribution $\pi$ of this chain is:

$$\pi_C = \frac{p_{IC}}{p_{IC} + p_{CI}}, \quad \pi_I = \frac{p_{CI}}{p_{IC} + p_{CI}}$$

As long as $p_{IC} > p_{CI}$, repeated self-evolving iterations guarantee convergence to a majority of correct solutions, regardless of the reliability of individual verification or refinement steps. This insight is critical for open-weight models, which often lack robust self-verification and correction mechanisms.

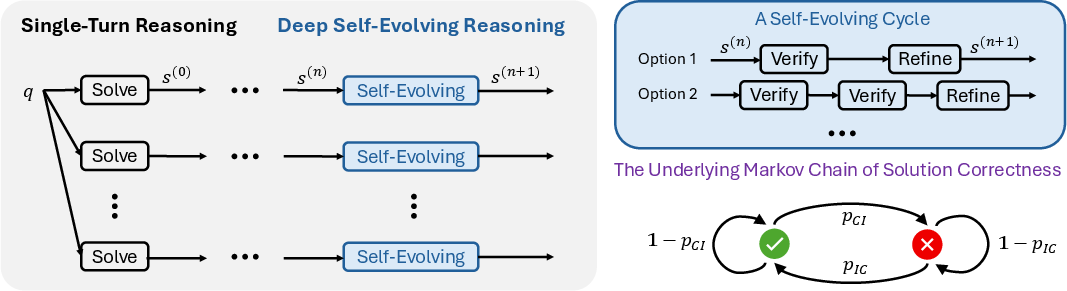
Figure 2: DSER framework overview—each "Solve", "Verify", and "Refine" block is a reasoning call; deep self-evolution is sufficient for hard problems.

Empirical Evaluation and Performance Analysis

The DSER framework is instantiated on DeepSeek-R1-0528-Qwen3-8B (DS-8B), an 8B-parameter model distilled from a 600B teacher. On the AIME 2024-2025 benchmarks, DS-8B initially fails to solve 9 out of 60 problems using standard majority voting over 128 parallel trials. Applying DSER, the model solves 5 of these 9 hard problems, including cases with zero initial Pass@1 accuracy. DSER also improves overall Pass@1 accuracy by 6.5% (AIME 2024) and 9.0% (AIME 2025), with majority-vote accuracy surpassing the teacher model's single-turn performance.

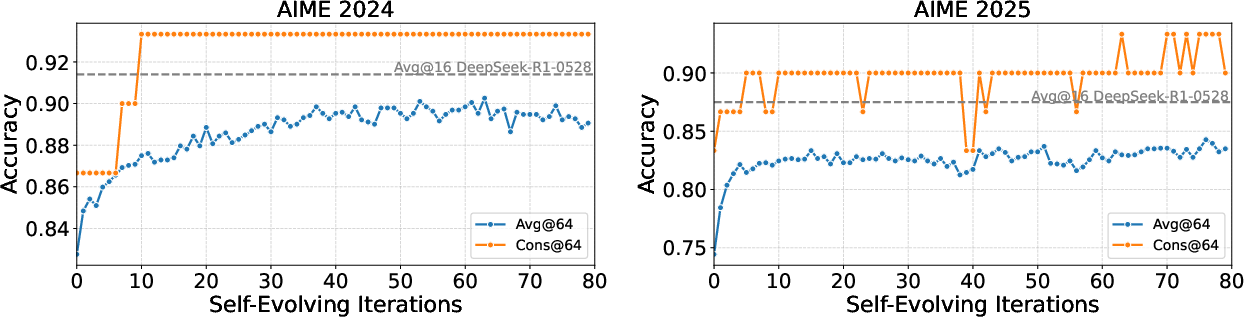
Figure 3: DSER boosts DS-8B's performance over iterations, with majority-vote accuracy exceeding the 600B teacher's Pass@1.

Per-question analysis reveals diverse convergence speeds and stationary distributions, reflecting the varying improvement probabilities across problems. Some problems exhibit rapid convergence to high correctness, while others converge slowly or stabilize at suboptimal distributions, highlighting the model's limitations in maintaining correct solutions for the hardest cases.

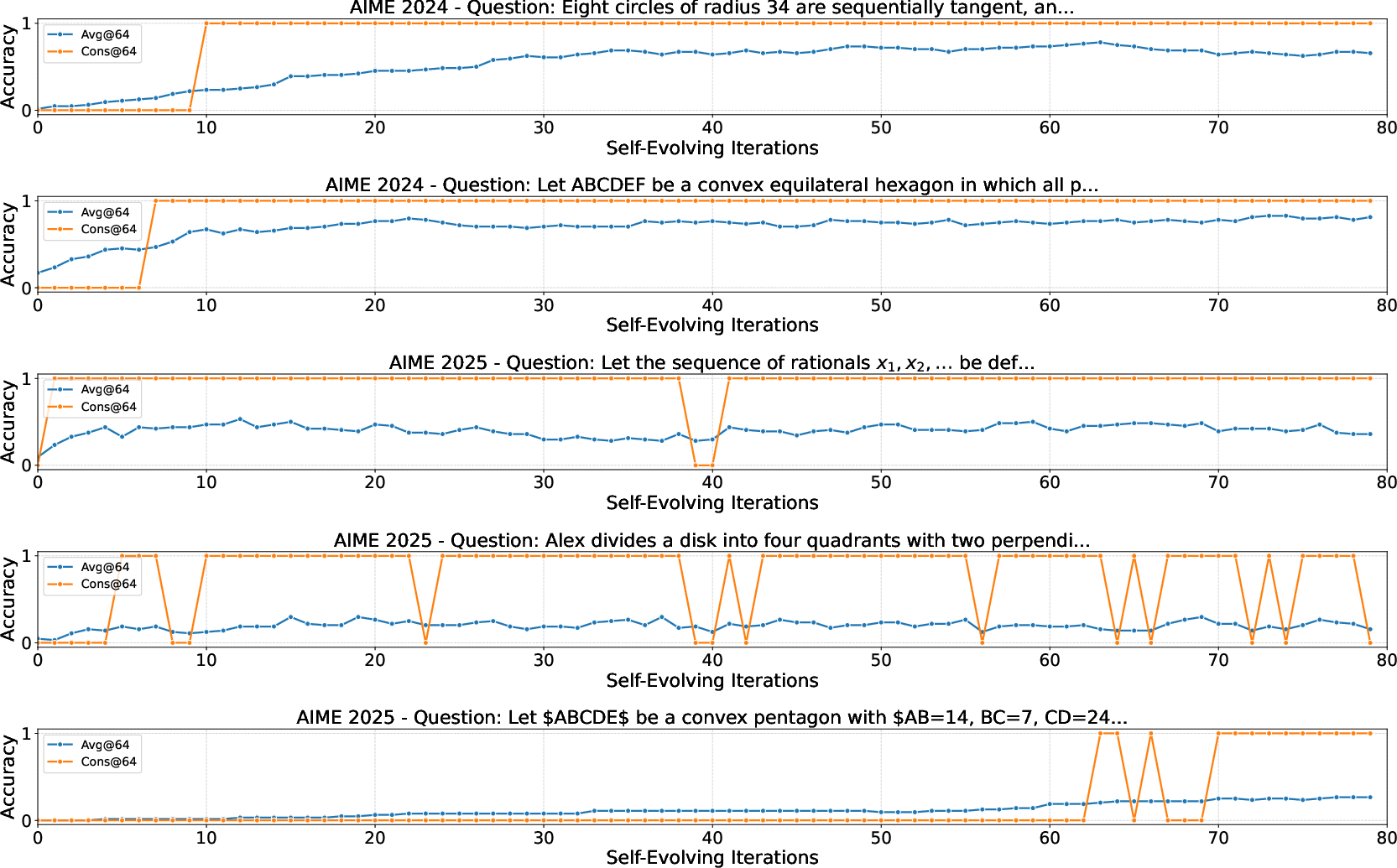
Figure 4: Per-question performance improvements on hard problems, illustrating different convergence rates and stationary distributions.

Comparison with Verification-Dependent Frameworks

The paper contrasts DSER with the verification-dependent self-evolving framework of Huang & Yang (Huang et al., 21 Jul 2025), which relies on absorbing states triggered by consecutive verification passes or failures. This design is analytically fragile for open-weight models: premature rejection exits and false-positive acceptances are common when verification is unreliable, leading to poor performance on hard problems.

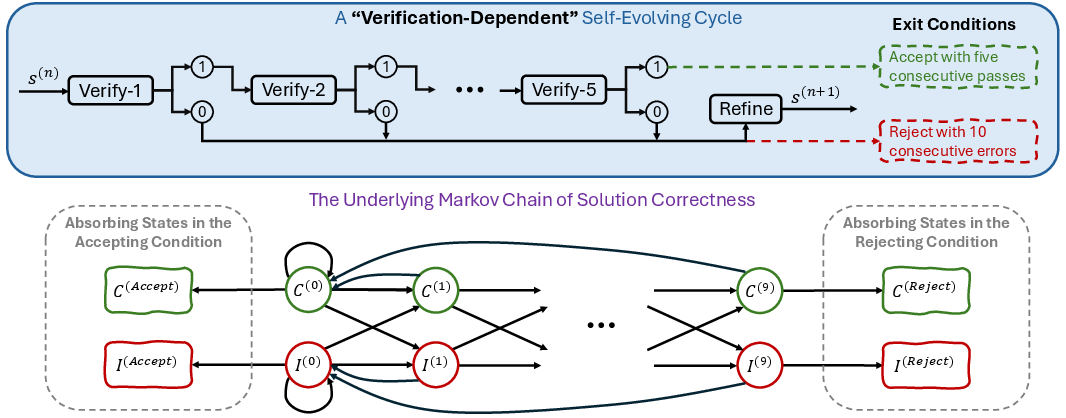
Figure 5: Markov chain analysis of verification-dependent iterative refinement, with multiple states indexed by consecutive rejections and refinements.

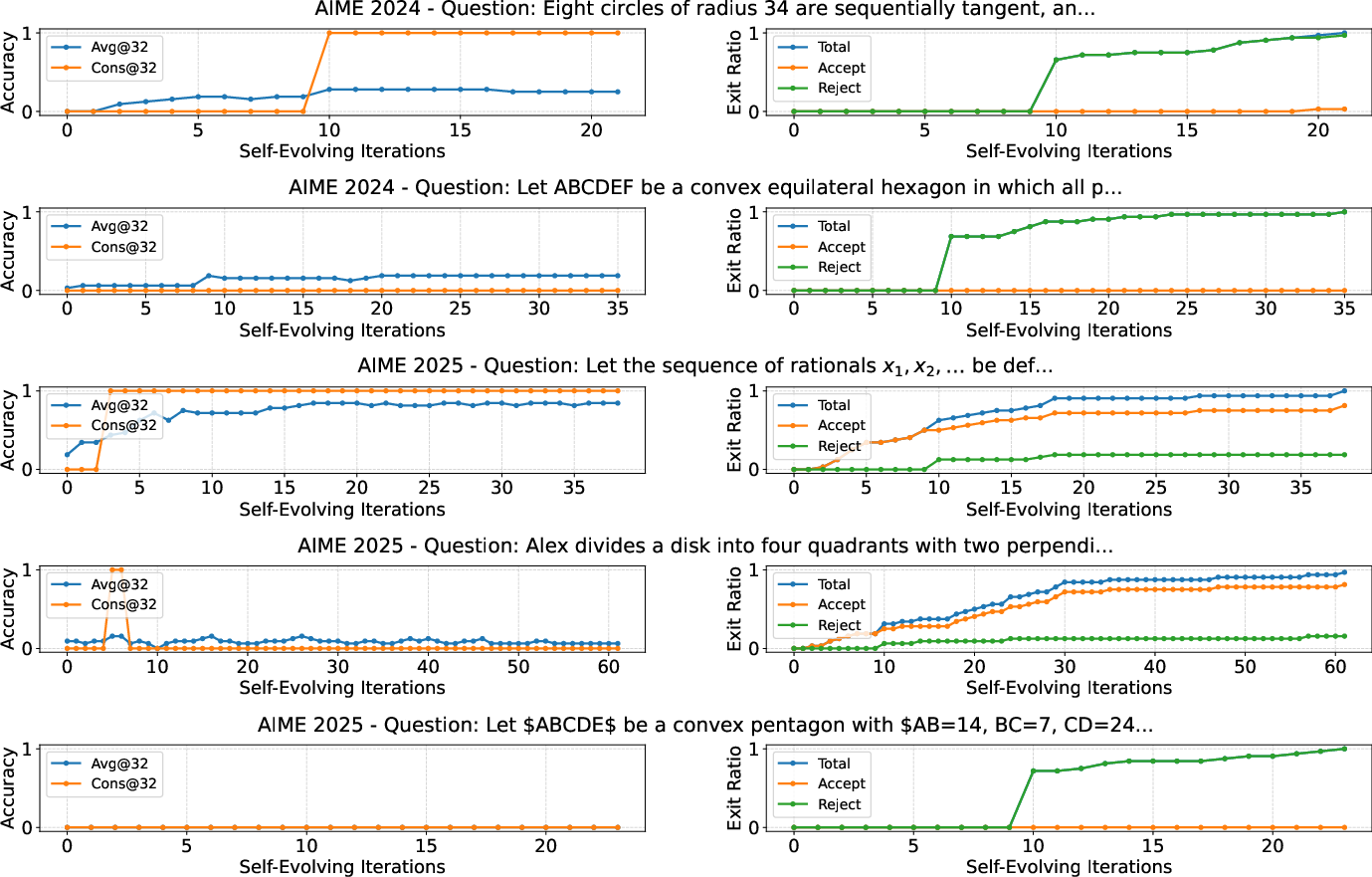
Figure 6: Verification-dependent self-evolving approach—per-question improvements and exit ratios, showing premature exits and limited success on hard problems.

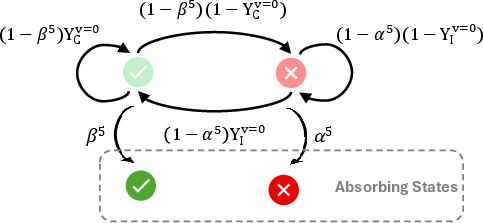
Figure 7: Simplified Markov transition graph for verification-dependent self-evolving, illustrating absorbing states and analytical intractability.

DSER, by marginalizing over verification outcomes and focusing on the statistical bias toward improvement, circumvents these limitations and achieves more stable, scalable reasoning.

Implementation Details

DSER is implemented via concise, model-agnostic prompts for verification and refinement. Each self-evolving iteration consists of:

• Verification Prompt: Requests step-by-step checking and a binary judgment.
• Refinement Prompt: Instructs the model to reconsider and correct its previous solution based on the verification report.

Parallel DSER processes are run for each problem, with majority voting over the final iterations to determine the answer. The approach is computationally intensive, requiring up to 10 million reasoning tokens for the hardest problems, but is highly parallelizable and agnostic to model architecture.

Theoretical and Practical Implications

The DSER framework provides a robust theoretical foundation for test-time scaling in LLMs, demonstrating that model capacity can be effectively traded for computation. It exposes the limitations of current open-weight models in self-verification and refinement, suggesting new directions for training objectives that explicitly optimize $p_{IC}$ and minimize $p_{CI}$. DSER can also be integrated into the exploration phase of RL-based reasoning algorithms (e.g., GRPO), potentially uncovering successful reasoning traces for extremely difficult tasks.

Future Directions

Key avenues for future research include:

• Training Objectives: Developing RL or SFT objectives that directly incentivize self-evolving capabilities, robust self-critique, and constructive correction.
• Framework Extensions: Incorporating advanced search algorithms, learnable verification modules, or adaptive iteration schedules to improve efficiency and success rates.
• Broader Applications: Applying DSER to other domains (e.g., code synthesis, theorem proving) and integrating with agentic tool-use frameworks.

Conclusion

DSER establishes a principled, probabilistic approach to deep iterative reasoning in LLMs, enabling open-weight models to solve problems previously deemed intractable. By leveraging the convergence properties of Markov chains and parallel computation, DSER unlocks latent reasoning capacity without requiring flawless stepwise execution. This paradigm shift from scaling model size to scaling inference-time computation is poised to drive the next generation of reasoning systems, bridging the gap between open-weight and proprietary models.