- The paper introduces an open-source theorem proving system that integrates verifier-guided self-correction and scaffolded data synthesis.
- It demonstrates that even smaller models (8B) can outperform larger counterparts through iterative self-correction and strategic model averaging.
- Benchmark results on MiniF2F and PutnamBench highlight significant performance gains, with self-correction consistently boosting proof accuracy.
Introduction
Goedel-Prover-V2 presents a series of open-source LLMs for automated theorem proving in Lean, achieving state-of-the-art performance with significantly reduced model size and computational requirements. The system is designed to generate complete formal proofs and iteratively refine them using verifier feedback, integrating innovations in data synthesis, self-correction, and model averaging. The flagship 32B model achieves 88.1% pass@32 on MiniF2F and 90.4% with self-correction, outperforming previous models such as DeepSeek-Prover-V2-671B and Kimina-Prover-72B, while the 8B variant surpasses DeepSeek-Prover-V2-671B despite being 80 times smaller.

Figure 1: Performance of Goedel-Prover-V2 on different benchmarks under pass@32.
Framework Innovations
Verifier-Guided Self-Correction
Goedel-Prover-V2 formalizes the integration of Lean compiler feedback into the proof generation loop. After an initial proof attempt, verification failures are parsed and fed back to the model, which then generates targeted repairs. This iterative self-correction process leverages error messages and tactic outcomes, enabling the model to diagnose and fix errors in long chain-of-thought (CoT) reasoning. Ablation studies confirm that compiler feedback is essential for effective revision, with removal of error messages resulting in significant performance degradation.
Scaffolded Data Synthesis
When the prover fails on a challenging problem, the extract_goal tactic in Lean is used to capture unsolved subgoals, which are then formalized as new, simpler statements. Both the extracted statements and their negations are added to the training set, enhancing the model's ability to distinguish true and false propositions.
LLMs are prompted to generate simpler subproblems or harder variants in natural language, which are then formalized into Lean statements. Quality control is enforced via LLM-based filters for correctness and difficulty, discarding trivial or incorrect statements and adding negations where appropriate. This pipeline accelerates data augmentation and ensures a diverse, high-quality training set.
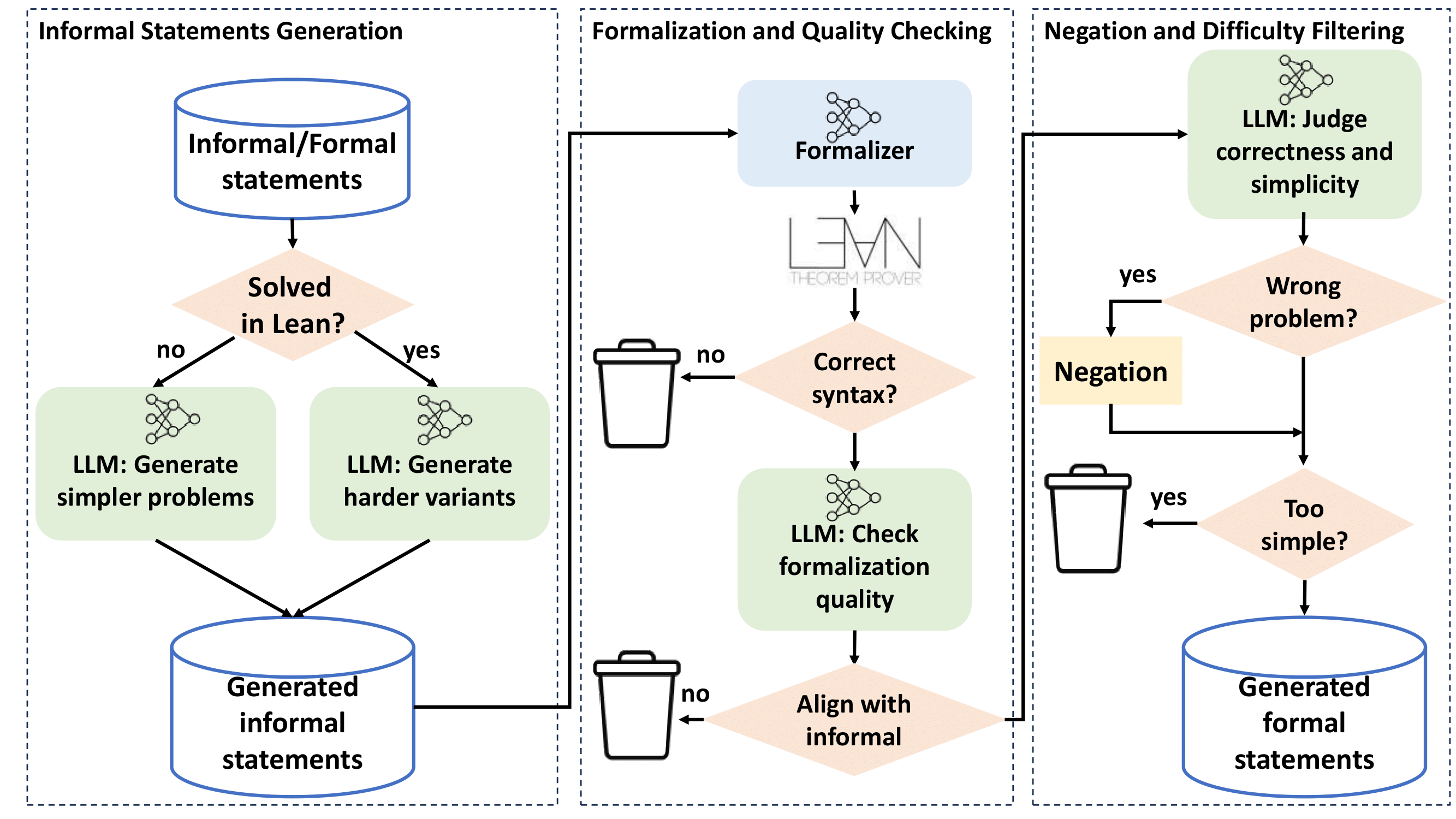
Figure 2: Our informal-based scaffolded data synthesis pipeline with three parts: (1) informal statement generation; (2) formalization and quality checking; and (3) negation and difficulty filtering.
Training Pipeline
The training process follows expert iteration, alternating between large-scale inference, supervised fine-tuning (SFT), and reinforcement learning (RL). Model averaging is applied after SFT and RL to mitigate diversity collapse, using a convex combination of base and fine-tuned model parameters. RL is implemented in a multi-task setup, optimizing both whole-proof generation and first-round self-correction, with dynamic sampling focused on problems of intermediate difficulty.
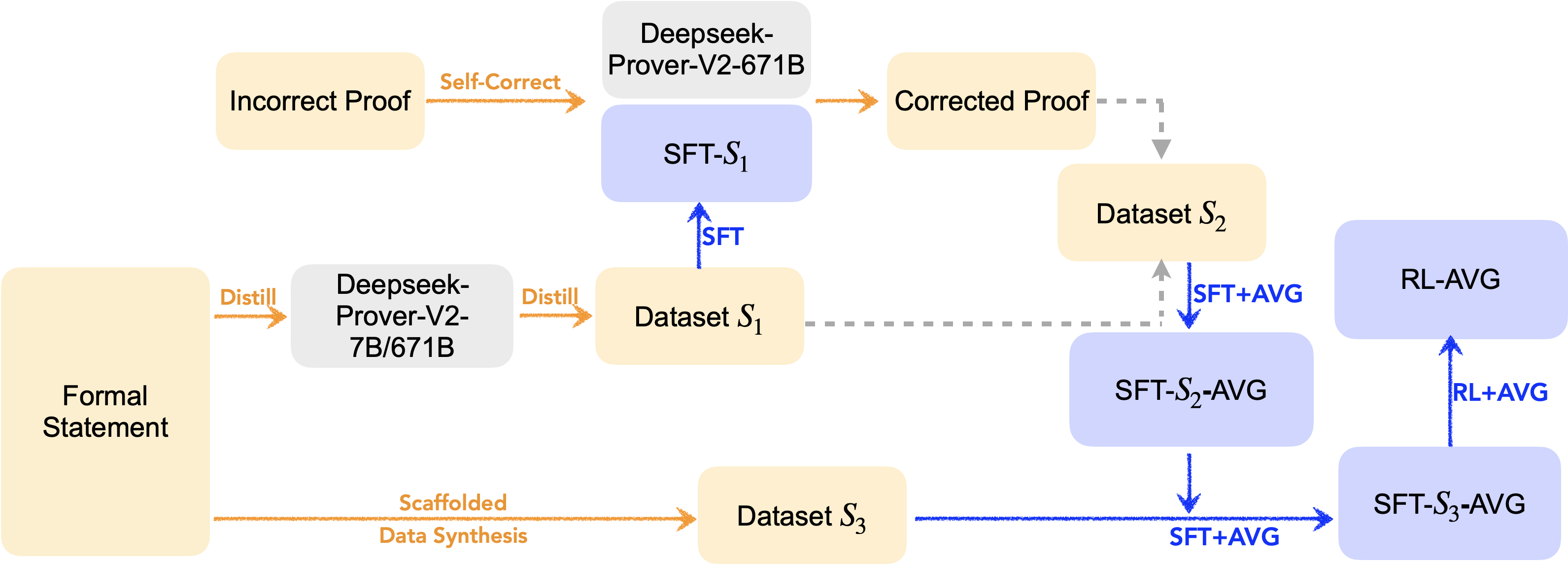
Figure 3: The overall workflow of model training. +AVG" denotes that the trained model is averaged with the base model after training.RL-AVG" is the final output model.
Evaluation and Results
Benchmarks
Goedel-Prover-V2 is evaluated on MiniF2F, PutnamBench, and MathOlympiadBench, covering high-school and college-level competition problems across diverse mathematical domains.

Figure 4: Distribution of problems in MathOlympiadBench by category.
Main Results
- MiniF2F: Goedel-Prover-V2-32B achieves 88.1% pass@32, rising to 90.4% with self-correction. The 8B model attains 84.6%, outperforming DeepSeek-Prover-V2-671B.
- PutnamBench: The 32B model solves 43 problems at pass@32, 57 with self-correction, and 86 at pass@184, surpassing DeepSeek-Prover-V2-671B's record of 47 at pass@1024.
- Sample Efficiency: High pass@N is achieved with minimal inference overhead, indicating strong internalization of reasoning strategies.
Scaling Analysis
Goedel-Prover-V2 demonstrates robust scaling behavior, maintaining superior accuracy across inference budgets. Self-correction consistently provides a 2-point gain in pass@32 and pass@64, with extended context and more revision iterations further improving sample efficiency.
RL and Model Averaging
Model averaging enhances diversity and pass@N, with optimal ratios maximizing performance. RL steps increase pass@1, while correction settings benefit more from RL due to the scarcity of high-quality self-correction data in SFT.
Implications and Future Directions
Goedel-Prover-V2 establishes that state-of-the-art formal theorem proving is achievable without massive models or proprietary infrastructure. The integration of verifier-guided self-correction with long CoT reasoning sets a new paradigm for efficient, scalable ATP. The open-source release of models, code, and data provides a foundation for further research in formal reasoning, proof repair, and inference-time scaling strategies.
The approach suggests several avenues for future work:
- Enhanced proof repair strategies leveraging subgoal extraction and targeted correction.
- Exploration of multi-turn RL and tool-use protocols for more complex revision loops.
- Extension to other formal systems and domains beyond Lean.
Conclusion
Goedel-Prover-V2 advances the frontier of automated theorem proving by combining scaffolded data synthesis, verifier-guided self-correction, and model averaging within a rigorous training pipeline. The models achieve state-of-the-art results on major benchmarks with modest computational resources, demonstrating that efficient, high-performance formal reasoning is attainable in open-source settings. The release of Goedel-Prover-V2 is poised to accelerate progress in AI-driven formal mathematics and provide a robust platform for future innovations.




