Back to Basics: Let Denoising Generative Models Denoise (2511.13720v1)

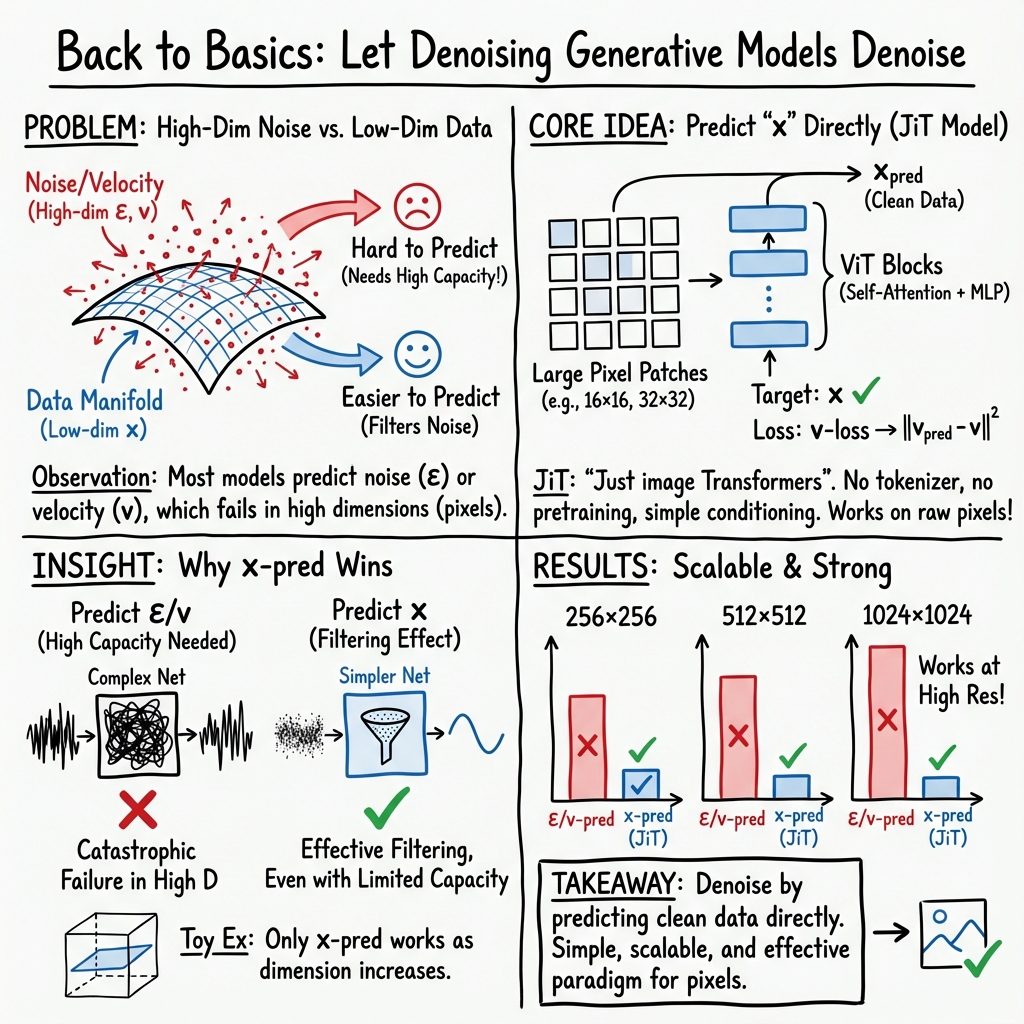
Abstract: Today's denoising diffusion models do not "denoise" in the classical sense, i.e., they do not directly predict clean images. Rather, the neural networks predict noise or a noised quantity. In this paper, we suggest that predicting clean data and predicting noised quantities are fundamentally different. According to the manifold assumption, natural data should lie on a low-dimensional manifold, whereas noised quantities do not. With this assumption, we advocate for models that directly predict clean data, which allows apparently under-capacity networks to operate effectively in very high-dimensional spaces. We show that simple, large-patch Transformers on pixels can be strong generative models: using no tokenizer, no pre-training, and no extra loss. Our approach is conceptually nothing more than "$\textbf{Just image Transformers}$", or $\textbf{JiT}$, as we call it. We report competitive results using JiT with large patch sizes of 16 and 32 on ImageNet at resolutions of 256 and 512, where predicting high-dimensional noised quantities can fail catastrophically. With our networks mapping back to the basics of the manifold, our research goes back to basics and pursues a self-contained paradigm for Transformer-based diffusion on raw natural data.

• The paper highlights that directly predicting clean data (x-prediction) leads to more tractable learning in high-dimensional settings than conventional noise predictions.
• Experimental results on synthetic and ImageNet data show that JiT models using x-prediction achieve superior FID scores and generate more coherent samples.
• The work advocates simpler transformer architectures without auxiliary losses, emphasizing manifold learning theory to enhance diffusion generative modeling.

Reconsidering Denoising Targets in Diffusion Models: An Expert Review

Abstract and Motivation

The paper "Back to Basics: Let Denoising Generative Models Denoise" (2511.13720) provides a critical reexamination of the ubiquitous practice in diffusion generative models of predicting noise or noised quantities, rather than directly predicting the clean data. Motivated by the manifold hypothesis—that natural signals reside on a low-dimensional manifold—this work hypothesizes that direct clean data prediction ($x$-prediction) is fundamentally more tractable, especially in high-dimensional pixel spaces, than conventional approaches such as $\epsilon$-prediction or $v$-prediction, which force the model to operate off-manifold. The authors demonstrate that even ostensibly under-complete models can perform well if restricted to $x$-prediction, and introduce the "Just image Transformers" (JiT) paradigm: plain Vision Transformers applied directly to large patches of pixel data, with no auxiliary losses, pre-training, or latent tokenization.

Background and Theoretical Analysis

The trajectory of diffusion generative models has moved from classical direct denoising—predicting clean samples from their corrupted versions—to reparameterizations wherein networks predict the noise ($\epsilon$) or flow velocity ($v$). Prior works have interpreted these parameterizations as equivalent under suitable loss reweightings, yet this paper elucidates that such equivalency breaks down in high-dimensional regimes. The low-dimensional manifold assumption, foundational in semi-supervised learning and representation learning, makes it clear that clean data and noise are categorically different targets for generative modeling: noise is spread throughout the full ambient space, while clean data is concentrated on a low-dimensional structure.

The authors formalize diffusion in terms of an interpolation between data and noise:

$z_t = t x + (1 - t) \epsilon$

and relate the different prediction targets through explicit mappings. They enumerate nine possible choices based on prediction and loss spaces ($x$, $\epsilon$, $v$), showing none are mathematically equivalent in practice. Crucially, the generator always operates by solving an ODE, but the choice of prediction space dictates the tractability of learning in extremely high-dimensional settings.

Experiments and Numerical Evidence

A series of toy experiments and ImageNet studies substantiate the theoretical claims. In synthetic setups where low-dimensional data is projected into a high-dimensional observed space via an unknown random projection, only $x$-prediction survives the curse of dimensionality as the observed space grows (Figure 1).

Figure 1: $d$-dimensional ($d=2$) underlying data is buried in a $D$-dimensional observed space. Only $x$-prediction recovers structure as $D$ increases.

On ImageNet at 256×256 and 512×512 resolution, using Transformers with patch sizes of 16 and 32, resulting in per-patch dimensions of 768 and 3072 respectively, only $x$-prediction yields strong FID scores and stable qualitative generations. Other parameterizations degrade catastrophically, even when the model's hidden dimension is much smaller than the input (patch) dimension.

Further analysis demonstrates that architectural modifications traditionally deployed to deal with high-dimensionality—such as increasing width, dense convolutions, or hierarchical patches—are only necessary when the model is tasked with off-manifold predictions. Conspicuously, bottleneck architectures with aggressively reduced linear embedding dimensions perform robustly when restricted to $x$-prediction, lending support to manifold learning theory.

JiT: Just Image Transformers for Diffusion

The practical instantiation of these insights is the JiT model—plain Vision Transformers applied to large pixel patches without pre-training or extra loss components. The architecture is fully self-contained and computes denoised outputs directly from the noised input and time step. Class conditioning is applied through standard methods, and further improvements leverage general-purpose Transformer upgrades (e.g., SwiGLU, RMSNorm, RoPE, qk-norm).

Comprehensive experiments demonstrate competitive FID scores at 256, 512, and 1024 resolution, scaling with model size and patch dimension but remaining robust even in regimes where the network width is significantly less than the patch dimension. JiT models outperform baseline pixel-space diffusion methods and rival the performance of latent diffusion methods despite greater simplicity and efficiency.

Figure 2: Qualitative examples from JiT-H/32 on ImageNet 512×512, evidencing visually coherent high-resolution samples without latent tokenization or auxiliary pre-training.

Loss Surface Analysis and Training Dynamics

Comparisons of convergence dynamics between $x$-prediction and $v$-prediction with the same loss reveal consistently lower training losses and fewer artifacts for $x$-prediction. Attempts to adapt techniques from EDM (preconditioning the network output) or to rescue catastrophic cases with aggressive noise-level shifts or greater model width are empirically ineffective.

Figure 3: Training loss and output images for $x$- and $v$-prediction, showing that $v$-prediction leads to higher loss and visible artifacts, even with matched loss space.

Implications and Future Directions

The findings reinstate first-principles manifold learning as a guiding paradigm for generative modeling in high-dimensional pixel space. By focusing network capacity on modeling clean data and leveraging architectural advances from general Transformers, diffusion generative models can be simplified while retaining competitive performance.

Practically, JiT obviates the need for pre-trained latent tokenizers and domain-specific components, opening avenues for generative modeling in scientific domains where raw data is high-dimensional and complex (e.g., protein folding, molecular generation, climate modeling). The approach encourages further scaling and transfer of Transformer progress to diffusion modeling, with potential for enhanced cross-domain applicability.

On a theoretical level, these results challenge the assumption of loss reweighting equivalence in high-dimensional network settings and highlight the need for a reexamination of standard training and inference protocols in generative modeling.

Conclusion

This work rigorously argues that diffusion models should return to predicting clean data, especially when operating in regimes of high-dimensional inputs. Empirical and theoretical evidence demonstrates that plain Transformers employing $x$-prediction can generate high-quality samples without architectural excesses or auxiliary components. This re-centering on the denoising objective and the adoption of task-agnostic model structures portend wider universality and efficiency for future generative frameworks across domains.