Is Your Conditional Diffusion Model Actually Denoising? (2512.18736v1)
Abstract: We study the inductive biases of diffusion models with a conditioning-variable, which have seen widespread application as both text-conditioned generative image models and observation-conditioned continuous control policies. We observe that when these models are queried conditionally, their generations consistently deviate from the idealized "denoising" process upon which diffusion models are formulated, inducing disagreement between popular sampling algorithms (e.g. DDPM, DDIM). We introduce Schedule Deviation, a rigorous measure which captures the rate of deviation from a standard denoising process, and provide a methodology to compute it. Crucially, we demonstrate that the deviation from an idealized denoising process occurs irrespective of the model capacity or amount of training data. We posit that this phenomenon occurs due to the difficulty of bridging distinct denoising flows across different parts of the conditioning space and show theoretically how such a phenomenon can arise through an inductive bias towards smoothness.
Sponsor
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper asks a simple question with big consequences: when a diffusion model is told to generate something based on a “condition” (like a text prompt or an extra input), does it really follow the clean, step‑by‑step “denoising” process the math says it should? The authors find that, in practice, conditional diffusion models often drift away from the ideal cleaning process. They introduce a new measurement, called Schedule Deviation, to track how much and how fast this drift happens, and explain why it occurs.
Key questions the paper explores
- Do conditional diffusion models follow the ideal, consistent “cleaning” (denoising) route from noise to a final sample?
- How can we measure when and where a model’s behavior departs from that ideal route?
- Does this drift go away with larger models or more training data?
- Can this drift explain why different sampling methods (like DDPM and DDIM) sometimes give noticeably different results?
- What causes the drift in the first place?
Methods and ideas explained simply
Think of diffusion models like a careful cleaning process:
- You start with a very noisy picture.
- At each small step, you remove some noise and sharpen the image.
- If you knew the perfect cleaning plan, you’d follow the same “path” every time, just with different small random variations.
Now add “conditioning”—extra information that guides what to clean toward. For example:
- Text describing “a dog in the park”
- A known target style
- Or a robot state that needs the next action
In theory, even with conditioning, the model should trace an ideal route from noise to the final result. But the authors find that real models don’t always do this.
Here’s what they introduce to study the problem:
Schedule Deviation (SD)
Schedule Deviation is a way to quantify how quickly a model’s actual “cleaning” path starts to differ from the ideal denoising path. You can think of it like a “drift meter”:
- If SD is small, the model’s steps align closely with the ideal cleaning route.
- If SD is large, the steps are steering off that route.
Why is SD useful?
- It doesn’t need access to the original training data or the true “perfect” score function.
- It can be computed using only the trained model and its own samples.
- It ties directly to how the model moves probability around during the cleaning process.
The authors also show that SD is mathematically linked to how different the entire path of generated samples becomes (in terms of probability), not just at one moment. That means SD is a meaningful, principled signal about path‑level inconsistency.
Datasets used to test SD
To make the ideas concrete and visual:
- MNIST and Fashion‑MNIST images conditioned on a 2D embedding (a simple stand‑in for text conditioning).
- A maze path‑planning task conditioned on start/end positions (so the model generates plausible routes).
They compare common samplers like DDPM and DDIM and measure how far their results differ using Earth Mover’s Distance (EMD)—imagine reshaping one pile of sand to match another, and the “effort” to move all the grains is the distance.
Main findings and why they matter
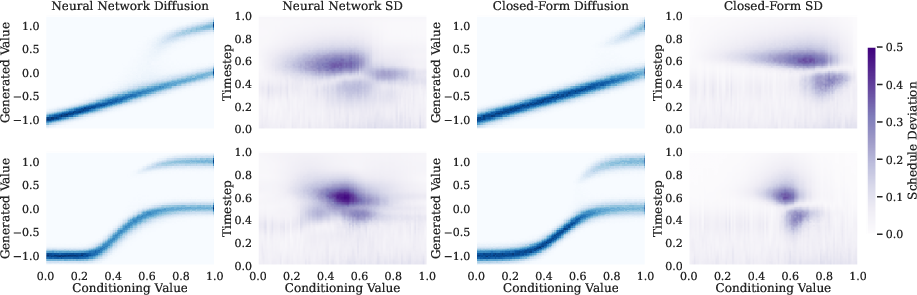
- Conditional models often are not strictly “denoising.”
- Across tasks and datasets, the Schedule Deviation is frequently non‑zero.
- That means the model’s actual cleaning steps depart from the ideal path, especially in the middle of the process (not at the beginning or end).
- Bigger models and more data don’t fully fix the issue.
- While capacity and data help a bit, SD often stays substantial.
- SD can vary a lot depending on the particular condition (e.g., different classes or prompts), even when those conditions are equally represented in training.
- SD predicts sampler disagreement (DDPM vs DDIM).
- Where SD is high, DDPM and DDIM produce more different samples.
- This makes sense: if the “ideal path” is not being followed, samplers that are supposedly equivalent in theory will diverge in practice.
- Why does the drift happen? Smoothness and “self‑guidance.”
- Neural networks tend to prefer smooth changes—especially with respect to the conditioning variable.
- The model blends guidance from nearby conditions (like mixing advice from similar prompts) instead of strictly following the denoiser for just one condition.
- The authors call this “self‑guidance” (similar in spirit to classifier‑free guidance): the learned flow at a condition becomes a combination of flows from neighboring conditions.
- Mathematically, combining flows like this does not match a single ideal denoising path, so drift is expected.
- Toy examples and theory back up the explanation.
- In settings where the condition is discrete (like a few prompt points), the model “fills in” the gaps using smooth interpolation (like cubic splines).
- In settings with a continuous condition (like a range of prompts), adding a smoothness penalty leads to a local averaging (a kind of “convolution”) over nearby conditions.
- Both mechanisms produce self‑guidance and, therefore, Schedule Deviation.
Implications and potential impact
- Be cautious when assuming all samplers (DDPM, DDIM, etc.) will behave the same. In practice, conditional models often drift from the ideal denoising path, and different samplers can then generate meaningfully different outputs.
- Schedule Deviation gives researchers and practitioners a practical tool to diagnose and understand where and why a model departs from denoising. That can guide:
- Better sampler design
- Training strategies that manage or exploit smoothness
- Debugging mismatches between sampling methods
- Understanding self‑guidance may help in applications like text‑to‑image, robotics, and scientific generation, where the condition matters a lot. Sometimes blending nearby conditions can be helpful; other times it causes unwanted artifacts. Knowing when SD is high lets you act accordingly.
In short, this paper shows that conditional diffusion models aren’t always doing pure “cleaning.” They often blend guidance across conditions due to a natural smoothness bias, and that blending explains why different sampling methods can disagree. Schedule Deviation shines a light on this hidden behavior and offers a way to measure and study it.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, actionable list of what remains missing, uncertain, or unexplored in the paper.
- High-dimensional scalability of Schedule Deviation (SD): quantify estimator variance, bias, and sample complexity when computing ∇·v and scores in high-dimensional x (e.g., 256×256 images); provide confidence intervals and convergence diagnostics.
- Sampler-dependence of p0 in SD computation: the paper estimates p0 using a particular sampler (e.g., DDPM), making SD potentially sampler-dependent; define a sampler-invariant or canonical way to obtain p0 or study SD’s sensitivity to the choice of sampler used to define p0.
- Sensitivity to diffusion schedules and objectives: systematically evaluate how SD changes across VP/VE schedules, EDM schedules, rectified flows, flow matching, and consistency training; clarify whether SD is an artifact of a specific schedule or a general phenomenon.
- Discretization confounds: isolate DDPM/DDIM disagreement due to schedule inconsistency from disagreement due to finite-step discretization errors; perform ablations over step counts and adaptive solvers to bound discretization effects.
- Generalization beyond low-res, low-dim conditioning: validate SD on large-scale, high-resolution text-to-image and video models (with realistic CLIP/text embeddings) and on policy models in control; test higher-dimensional z to assess whether the phenomenon persists.
- t-SNE conditioning limitations: t-SNE distorts global geometry of z; repeat experiments with semantically meaningful, metric-preserving embeddings (e.g., CLIP, supervised attribute encoders) and quantify how geometry of z influences SD.
- Unconditional setting: measure and compare SD in unconditional models to establish whether schedule inconsistency is uniquely conditional or also prevalent without conditioning.
- Architectural and training dependencies: go beyond U-Nets—evaluate transformers, DiT-like backbones, attention variants, and different conditioning mechanisms (FiLM, cross-attention) to identify which design choices amplify or reduce SD.
- Relation to sample quality: rigorously test whether higher SD correlates with (or causally affects) FID, precision/recall, and human preference; clarify if SD is detrimental, beneficial, or neutral to perceptual quality.
- Mitigation strategies: design and evaluate training-time regularizers (e.g., denoiser self-consistency losses, SD-penalty surrogates) and their trade-offs with sample quality and speed; determine whether SD can be reduced without degrading fidelity/diversity.
- Theoretical assumptions: current analyses rely on discrete support or uniform p(z) and smoothness penalties; generalize to non-uniform, high-dimensional p(z), realistic z geometries, and non-convex implicit biases induced by SGD and network architectures.
- Multimodality–SD link: provide rigorous conditions connecting multimodality/topological complexity of p(x|z) to necessary SD; characterize when self-guidance necessarily induces non-denoising flows.
- Alternative path discrepancy metrics: compare SD to KL-based path discrepancy, integral probability metrics, and pathwise Wasserstein; quantify tightness and calibration of the TV bounds and identify regimes where SD is most informative.
- Efficient SD estimation: develop scalable estimators that avoid explicit divergence computation (e.g., Hutchinson tricks with variance control, score-matching surrogates); provide error bounds and computational budgets for practical use.
- Robustness across samplers: extend SD–disagreement analysis to DPM-Solver, ODE solvers, ancestral samplers, consistency sampling, and varying noise/discretization schedules; quantify consistency of the observed correlations.
- Guidance effects: measure SD under classifier-free guidance across guidance scales and other guidance schemes; determine whether guidance systematically increases/decreases schedule inconsistency and why.
- Time-local analysis: decompose SD over s to identify which timesteps contribute most; study whether re-timing, schedule warping, or adaptive step allocation can reduce high-SD phases.
- Data quantity and class imbalance: provide controlled experiments explaining non-monotonic SD vs. data size and class-dependent SD; determine whether data curation (balancing, augmentation) systematically affects SD.
- Detecting self-guidance in trained models: devise probes to test whether learned flows are linear/nonlinear combinations of neighboring-z flows; validate the self-guidance hypothesis in real networks beyond toy settings.
- Conditioning mechanism choices: study how specific conditioning implementations (FiLM, cross-attention, concatenation) alter the smoothness bias in z and thereby SD; recommend conditioning designs that mitigate SD.
- Loss parameterization effects: assess SD under ε-prediction, v-prediction, and x0-prediction parameterizations and across different noise level parameterizations; determine which choices are more schedule-consistent.
- Downstream task impacts: for control/trajectory generation, quantify how SD influences policy performance, safety, and robustness; for image editing/inversion tasks, assess whether SD affects edit fidelity or inversion stability.
- Reparameterization of z: analyze how SD behaves under nonlinear reparameterizations of the conditioning (e.g., t-SNE, PCA, isotropic scalings); propose z-invariant or geometry-aware SD variants.
- SD-aware samplers: design samplers that remain close to the model’s IMCF even when v deviates (e.g., correcting drift to track the intended path); test whether such samplers reduce cross-sampler disagreement.
- Statistical rigor of correlations: report formal correlation metrics, uncertainty estimates, and hypothesis tests for SD vs. OT-distance relationships; verify reproducibility across seeds, datasets, and training runs.
- Simplified SD on CelebA: the divergence-free SD proxy used for CelebA is noisy and unvalidated; quantify the bias introduced by omitting ∇·v, identify when this proxy is acceptable, and propose improved high-dim approximations.
Glossary
Below is an alphabetical list of advanced domain-specific terms used in the paper, each with a short definition and a verbatim usage example.
- Bezier curve: A parametric curve commonly used to model smooth paths and shapes; here used to smoothly fit maze trajectories. "smooth Bezier curve fit to the path"
- Classifier-free guidance: A sampling technique that linearly combines conditional and unconditional diffusion guidance to steer generation. "Prior work has shown that classifier-free guidance causes the resulting diffusion to no longer constitute a denoising process"
- Consistency distillation: A training approach that enforces agreement between few-step generators and the integrated ODE flow induced by a model’s velocity field. "Consistency distillation enforces a related condition: that a few-step model is consistent with the integrated flow map of the ODE induced by the flow-field "
- Consistency Models: A class of models trained to produce consistent outputs across steps; distinct from the paper’s notion of schedule consistency. "our notion of consistency is unrelated to that of Consistency Models"
- Conditional diffusion models: Diffusion models whose generation depends on a conditioning variable (e.g., text or observations). "Conditional diffusion models routinely and consistently deviate from the idealized model-consistent diffusion probability path, $$."</li> <li><strong>Conditional normalizing flow</strong>: A flow-based generative model where the flow and densities are conditioned on an external variable. "We say $(v,p)vp_s$ of the probability path"</li> <li><strong>DDIM</strong>: Deterministic Diffusion Implicit Models, a popular diffusion sampling method with reduced stochasticity. "inducing disagreement between popular sampling algorithms (e.g. DDPM, DDIM)."</li> <li><strong>DDPM</strong>: Denoising Diffusion Probabilistic Models, a canonical stochastic diffusion sampler. "inducing disagreement between popular sampling algorithms (e.g. DDPM, DDIM)."</li> <li><strong>Denoising training objective</strong>: The objective that trains diffusion models to predict and remove noise, stabilizing generative training. "via the denoising training objective"</li> <li><strong>Dirac delta</strong>: A generalized function representing an infinitely concentrated point mass, used in analysis of limiting behavior. "behaves like a Dirac $\updeltaz$"</li> <li><strong>Earth Mover Distance (EMD)</strong>: A metric (1-Wasserstein) for measuring distributional differences via optimal transport. "as measured by $1$-Wasserstein/Earth-Mover-Distance"</li> <li><strong>Flow-based generative models</strong>: Models that generate data by evolving samples through a continuous-time velocity (flow) field. "Flow-based generative models parameterize a time-varying family of conditional densities $p_s(x | z), s \in [0,1]$"</li> <li><strong>Frobenius norm</strong>: A matrix norm equal to the square root of the sum of squared entries; here used to penalize curvature in the conditioning variable. "with respect to the Frobenius norm of the appropriate Hessian:"</li> <li><strong>Gradient-Estimation (GE) sampling algorithm</strong>: A diffusion sampling method that estimates gradients to improve sampling efficiency. "such as the Gradient-Estimation (GE) sampling algorithm \citep{permenter2023interpreting}"</li> <li><strong>Hessian</strong>: The matrix of second derivatives (curvatures) of a function; used to regularize smoothness over the conditioning variable. "the joint Hessian $\nabla_{x,z}^2 v(x,z)$"</li> <li><strong>Ideal Model-Consistent Flow (IMCF)</strong>: The unique velocity-minimizing flow whose induced path matches the model’s diffusion probability path. "The ideal denoising diffusion flow (IMCF) of $\hat{p}$"</li> <li><strong>Langevin dynamics</strong>: A stochastic process that performs gradient ascent on log-density with noise; used to analyze guidance mechanisms. "alternatively, as a combination of Langevin dynamics on the weighted product distribution"</li> <li><strong>Manifold of equiprobable density</strong>: The set of points with equal probability density, used to interpret certain guidance mechanisms. "either sampling from the manifold of equiprobable density"</li> <li><strong>Ordinary Differential Equation (ODE)</strong>: A deterministic continuous-time formulation for diffusion inference and sampling. "Ordinary Differential Equation (ODE) \citep{karras2022elucidating} formalisms"</li> <li><strong>Optimal transport distance</strong>: A measure of distributional difference based on the minimal cost of transporting mass between distributions. "optimal transport distance between DDPM/DDIM samples"</li> <li><strong>Performance Difference Lemma</strong>: A result from reinforcement learning relating performance gaps to occupancy measures; used to motivate SD bounds. "closely resembles the formulation of the classical Performance Difference Lemma in Reinforcement Learning"</li> <li><strong>Probability path</strong>: The time-indexed family of marginal densities produced by a flow-based generative model. "marginal densities $p_s$ of the probability path"</li> <li><strong>Schedule Deviation (SD)</strong>: A metric quantifying how a model’s flow instantaneously departs from its ideal denoising diffusion path. "We introduce Schedule Deviation (SD), our new metric which quantifies the extent to which a diffusion model (conditional or otherwise) deviates from the idealized diffusion probability path"</li> <li><strong>Score function</strong>: The gradient of the log-density, used to express diffusion flows and guide sampling. "represents the MCF in terms of the score functions $\nabla_x \log p_s(x \mid z)$"</li> <li><strong>Self-guidance</strong>: An implicit guidance phenomenon where conditional flows are locally combined across conditioning values due to smoothness bias. "we term ``self-guidance," can naturally arise"</li> <li><strong>Stochastic Differential Equation (SDE)</strong>: A stochastic continuous-time formulation for diffusion inference and sampling. "Stochastic Differential Equation (SDE) \citep{ho2020denoising}"</li> <li><strong>Stochastic interpolants</strong>: A framework that represents diffusion paths as stochastic mixtures of signal and noise schedules. "The stochastic interpolants framework \citep{albergo2023stochastic} provides an alternative description for flow-based models"</li> <li><strong>Tangent process</strong>: A stochastic process that initially matches a reference path and then evolves under a potentially different flow. "We refer to the random variable $X^v_{s|t}$ as a tangent process \citep{falconer2003local}"</li> <li><strong>Total Schedule Deviation</strong>: The aggregated Schedule Deviation across time, summarizing overall path inconsistency. "We additionally define the Total Schedule Deviation of $vz \in Z$"</li> <li><strong>Total variation distance</strong>: A measure of difference between probability distributions based on their maximum discrepancy over events. "closely related to the average total variation distance between path measures"</li> <li><strong>Transport equation</strong>: A continuity equation relating density evolution to divergence of the flow; used to compute SD. "can be efficiently evaluated as a consequence of the transport equation (\Cref{prop:easy_sd})."</li> <li><strong>t-SNE embedding</strong>: A nonlinear dimensionality reduction technique used to construct low-dimensional conditioning variables. "we condition on the t-SNE embedding of the images"</li> <li><strong>U-Net architecture</strong>: A convolutional neural network with skip connections, widely used as the backbone for diffusion models. "We use a U-Net architecture similar to \cite{dhariwal2021diffusion}"</li> <li><strong>Wasserstein distance (1-Wasserstein)</strong>: An optimal transport metric equivalent to EMD under certain cost functions. "as measured by $1$-Wasserstein/Earth-Mover-Distance"
Practical Applications
Below are practical, real-world applications grounded in the paper’s findings, methods, and innovations. Each item is an actionable use case and includes sector links and feasibility notes.
Immediate Applications
- Diagnostic metric for conditional diffusion reliability
- Sector: software/MLOps, generative media, robotics
- Use Schedule Deviation (SD) to continuously monitor when a conditional diffusion model’s generations depart from ideal denoising, and flag “risky” conditioning regions. Deploy as a model-health indicator in training and inference dashboards, similar to drift or calibration metrics. (Assumptions/Dependencies: access to model’s velocity/score outputs or the ability to estimate them; added compute for divergence and score estimation; chosen diffusion schedule must match production sampler.)
- Adaptive sampler routing at inference
- Sector: creative tools (text-to-image/video), robotics simulation/planning, molecule design
- Predict DDPM/DDIM (or other sampler) disagreement from SD and automatically pick the sampler or noise level per conditioning input to reduce artifacts and improve stability. Implement a “sampler router” that selects DDPM vs DDIM or hybrid schemes based on prompt-level SD scores. (Assumptions/Dependencies: reliable per-prompt SD estimation; thresholds calibrated against downstream quality metrics; minimal latency overhead.)
- Prompt/condition stability feedback for end users
- Sector: daily life (creators), education (teaching diffusion), media apps
- Show a “stability meter” next to the prompt or conditioning embedding that warns users when generation is likely to be inconsistent across samplers or vary across runs. Provide suggestions (e.g., adjust guidance strength, rephrase prompts, tweak conditioning embeddings). (Assumptions/Dependencies: mapping from text to conditioning vectors; UX integration; empirical calibration of SD-to-quality mappings.)
- Dataset curation and coverage mapping
- Sector: academia, industry (data engineering), healthcare imaging pipelines
- Use SD heatmaps over the conditioning space to identify sparse or multimodal regions that induce high deviation; prioritize targeted data collection or create local submodels for those regions. Incorporate SD into dataset acceptance tests. (Assumptions/Dependencies: robust conditioning-space representation—e.g., t-SNE/CLIP embeddings; SD does not necessarily decrease with more data—balance vs structure matters.)
- Reliability triggers in observation-conditioned control
- Sector: robotics/autonomy, industrial automation
- Monitor SD during policy inference; if SD exceeds a threshold, switch to a conservative controller or classical planner (fail-safe), or slow down and request human oversight. (Assumptions/Dependencies: real-time SD estimation feasible; policy’s inference stack exposes velocity/score outputs; latency budgets and safety certification constraints.)
- Reproducibility planning and sampler policy
- Sector: research labs, enterprise ML governance
- Precompute SD profiles to anticipate sampler-induced variability and set organizational defaults (e.g., DDPM for high-SD regions, DDIM otherwise) to improve experiment reproducibility and auditability. (Assumptions/Dependencies: SD correlates with sampler differences in your domain; standardized diffusion schedules across teams.)
- Training-time model selection and ablations
- Sector: academia, ML engineering
- Use SD as a validation metric alongside FID, EMD, and task metrics to compare architectures, guidance strengths, schedules, and data augmentation. Enable early stopping or hyperparameter search guided by SD trends. (Assumptions/Dependencies: compute overhead; stable SD estimation across seeds; alignment between chosen schedule and training objective.)
- Out-of-distribution (OOD) conditioning detection
- Sector: healthcare (conditional augmentation), finance (scenario generation), safety-critical simulations
- Treat sustained high SD for certain conditions as a signal of problematic bridging across conditioning space; gate or quarantine such requests and apply additional verification or human review. (Assumptions/Dependencies: careful thresholding to avoid false positives; domain-specific validation workflows.)
Long-Term Applications
- Schedule-consistent training objectives
- Sector: ML research, platform tooling
- Develop differentiable losses that penalize SD (e.g., transport-equation residuals vs the model-consistent IMCF), yielding models that remain close to true denoising paths under conditioning. Package as a training library extension for PyTorch/TF. (Assumptions/Dependencies: efficient SD approximation during training; stability of added regularizers; theoretical guarantees for convergence.)
- Samplers robust to schedule deviation
- Sector: generative media, robotics/control, molecular design
- Design new samplers that explicitly correct for v–IMCF mismatch (e.g., add divergence-based correction terms or use transport-informed updates) or orchestrate mixtures-of-samplers tailored to local SD profiles. (Assumptions/Dependencies: theory and empirical validation; potential extra steps/compute; integration with existing diffusion schedules.)
- Model governance standards and “schedule-consistency” reporting
- Sector: policy/regulation, enterprise AI governance
- Establish SD profiling as part of model cards and compliance documentation; require disclosure of SD distributions across conditioning space, sampler disagreement statistics, and mitigation policies in consumer-facing generative systems. (Assumptions/Dependencies: community consensus, standard SD estimation protocol; auditability of conditioning representations.)
- Safety certification for conditional diffusion in critical domains
- Sector: healthcare imaging, aviation/automotive autonomy, energy grid operations
- Use SD bounds and runtime monitors to define safety envelopes for conditional generation or control policies (e.g., trigger fallbacks if SD spikes). Integrate into formal verification toolchains. (Assumptions/Dependencies: formal bounds linking SD to risk; low-latency monitors; regulators accept SD-based criteria.)
- Conditioning-aware architectures and data curricula
- Sector: ML platform engineering, industry R&D
- Build mixture-of-experts or region-specific submodels to avoid brittle cross-region smoothing (“self-guidance”); design curricula that progressively cover multimodal conditioning regions to reduce bridging difficulty. (Assumptions/Dependencies: high-quality conditioning space partitioning; training orchestration; extra parameter count and serving complexity.)
- Interactive prompt-space analytics
- Sector: creative tools, content moderation
- Provide SD heatmaps and self-guidance diagnostics over prompt embeddings to guide prompt engineering and identify risky prompt regions (e.g., likely to produce unstable or divergent outputs). (Assumptions/Dependencies: reliable embedding space; visualization scaling to large vocabularies; privacy concerns.)
- Consistency distillation with SD constraints
- Sector: software tooling, accelerated inference
- Combine consistency models with SD-penalization to produce few-step samplers that remain schedule-consistent, reducing disagreement across samplers and speeding up inference. (Assumptions/Dependencies: co-design of distillation objective; compatibility with existing CM frameworks; empirical tuning.)
- Reliability SLAs for generative services
- Sector: cloud ML platforms, enterprise IT
- Incorporate SD thresholds into service-level objectives; route high-SD workloads to more conservative paths or require extra validation; log SD alongside outputs for audit trails. (Assumptions/Dependencies: monitoring infrastructure; customer acceptance of variable latency/quality in high-SD cases.)
- Managing hallucination and self-guidance
- Sector: media/content creation, scientific simulation
- Use SD to detect when the model is likely mixing flows from disparate conditioning regions (self-guidance); adapt guidance strength or apply local models to maintain fidelity. (Assumptions/Dependencies: mechanisms to control guidance strength per sample; robust local gating.)
- Benchmarks and leaderboards for schedule deviation
- Sector: academia/open-source
- Create standardized datasets and metrics focused on SD and sampler divergence, encouraging models and samplers that remain consistent under conditioning. (Assumptions/Dependencies: community adoption; open-source evaluation tooling; reproducible conditioning embeddings.)
Notes on feasibility across applications:
- SD estimation requires sampling from the model and computing divergence and scores over generated samples; this is computationally intensive and depends on the chosen diffusion schedule.
- The paper’s empirical findings show SD can persist even with more data and larger models; improving SD may require architectural or objective changes, not just scale.
- Mapping text prompts to conditioning vectors (e.g., CLIP or t-SNE of attributes) impacts SD structure and should be selected carefully for production systems.
Collections
Sign up for free to add this paper to one or more collections.