2000 character limit reached
Less is More: Recursive Reasoning with Tiny Networks (2510.04871v1)
Published 6 Oct 2025 in cs.LG and cs.AI
Abstract: Hierarchical Reasoning Model (HRM) is a novel approach using two small neural networks recursing at different frequencies. This biologically inspired method beats LLMs on hard puzzle tasks such as Sudoku, Maze, and ARC-AGI while trained with small models (27M parameters) on small data (around 1000 examples). HRM holds great promise for solving hard problems with small networks, but it is not yet well understood and may be suboptimal. We propose Tiny Recursive Model (TRM), a much simpler recursive reasoning approach that achieves significantly higher generalization than HRM, while using a single tiny network with only 2 layers. With only 7M parameters, TRM obtains 45% test-accuracy on ARC-AGI-1 and 8% on ARC-AGI-2, higher than most LLMs (e.g., Deepseek R1, o3-mini, Gemini 2.5 Pro) with less than 0.01% of the parameters.
Summary
- The paper introduces the Tiny Recursive Model (TRM), which significantly reduces network complexity while maintaining competitive reasoning performance.
- It employs recursive updates of latent variables and predictions using a simple two-layer architecture to prevent overfitting and minimize computational overhead.
- Empirical evaluations on puzzles like Sudoku and Maze demonstrate TRM's robustness and superior generalization compared to hierarchical reasoning models.
Tiny Neural Networks for Recursive Reasoning
Introduction
"Less is More: Recursive Reasoning with Tiny Networks" introduces the Tiny Recursive Model (TRM), a simplified approach for recursive reasoning tasks. This model stands out by its ability to achieve higher generalization with significantly fewer parameters compared to existing Hierarchical Reasoning Models (HRM). TRM employs small two-layer networks and recursive techniques to solve challenging reasoning tasks such as Sudoku, Maze, and ARC-AGI with remarkable efficiency.
Figure 1: Tiny Recursion Model (TRM) recursively improves its predicted answer with a tiny network. It starts with the embedded input question and initial embedded answer , and latent .
Recursive Reasoning with Tiny Networks
The TRM demonstrates a paradigm shift by reducing network complexity while maintaining competitive performance. It utilizes a single recursion model instead of HRM’s dual-network structure, focusing on recursive improvements of predictions. The primary operations in TRM include recursively updating latent variables and subsequently refining predicted answers. This recursion significantly reduces computational overhead and overfitting while remaining parameter-efficient.
Model Architecture and Mechanisms
TRM operates with a tiny network containing merely 7 million parameters, employing a two-layer architecture. The recursive process iteratively enhances the latent variables and predictions. Each input is transformed into an embedded form that undergoes multiple improvement steps. Unlike HRM, which insists on hierarchically processing inputs with multiple networks, TRM maintains simplicity without compromising on task performance.
Key to its operation is avoiding reliance on complex theoretical constructs such as the Implicit Function Theorem. Instead, TRM utilizes full recursive processes, inherently enhancing the model’s knowledge retention and task accuracy over multiple iterations. This method negates the necessity for stringent fixed-point convergence conditions often problematic in hierarchical models.
Algorithmic Efficiency and Deep Supervision
TRM employs a form of deep supervision to counteract overfitting, iterating over embedded features, allowing the model to generalize effectively across tasks. The model capitalizes on a simplified adaptive computational time (ACT) strategy to optimize training efficiency, eliminating the need for excessive forward passes typical in HRM implementations.
An innovative aspect is the removal of redundant ACT computations, thus maintaining computational economy during both training and inference phases. By leveraging exponential moving averages (EMA), TRM stabilizes learning trajectories, which is particularly beneficial in data-scarce environments.
Evaluation and Performance
TRM demonstrated superior generalization in various challenging benchmarks, notably achieving increased accuracy across complex puzzles while maintaining reduced computational requirements. The rigorous ablation studies underscore TRM’s robustness, affirming its superiority over conventional HRM counterparts.
Conclusion
TRM exemplifies an efficient recursive reasoning framework, breaking new ground in achieving high performance with minimal architectural overhead. Its simplicity belies its capability, making TRM a compelling option for resource-constrained AI applications. Future developments may explore extensions into broader generative tasks, with TRM offering a promising foundation for continued advances in computational reasoning paradigms.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper introduces a new way for small AI models to solve tough puzzles (like Sudoku, mazes, and ARC-AGI tasks). The main idea is simple: instead of trying to get the right answer in one shot, a tiny model makes a guess and then improves it step by step. The authors call this approach the Tiny Recursive Model (TRM). Even though TRM is small, it beats bigger, famous AI models on several hard puzzles.
What questions does the paper try to answer?
The paper asks:
- Can a small, simple AI model solve hard reasoning puzzles by improving its answers in steps?
- Do we really need huge LLMs and long “chains of thought” to reason well?
- Can we make the process simpler than previous methods (like HRM) and still get better results?
How does the method work? (Explained with everyday analogies)
Think of solving a puzzle like editing an essay:
- First, you write a rough draft (an initial answer).
- Then, you read it, think, and fix mistakes.
- You repeat this a few times until it looks good.
TRM does the same thing with a tiny neural network:
- Neural networks are math systems with “knobs” called parameters. More parameters usually mean a bigger model. TRM has around 7 million parameters—very small compared to giant LLMs with billions or trillions.
- Recursion means “do a process, then use its result to do it again.” TRM uses recursion to improve its answer repeatedly.
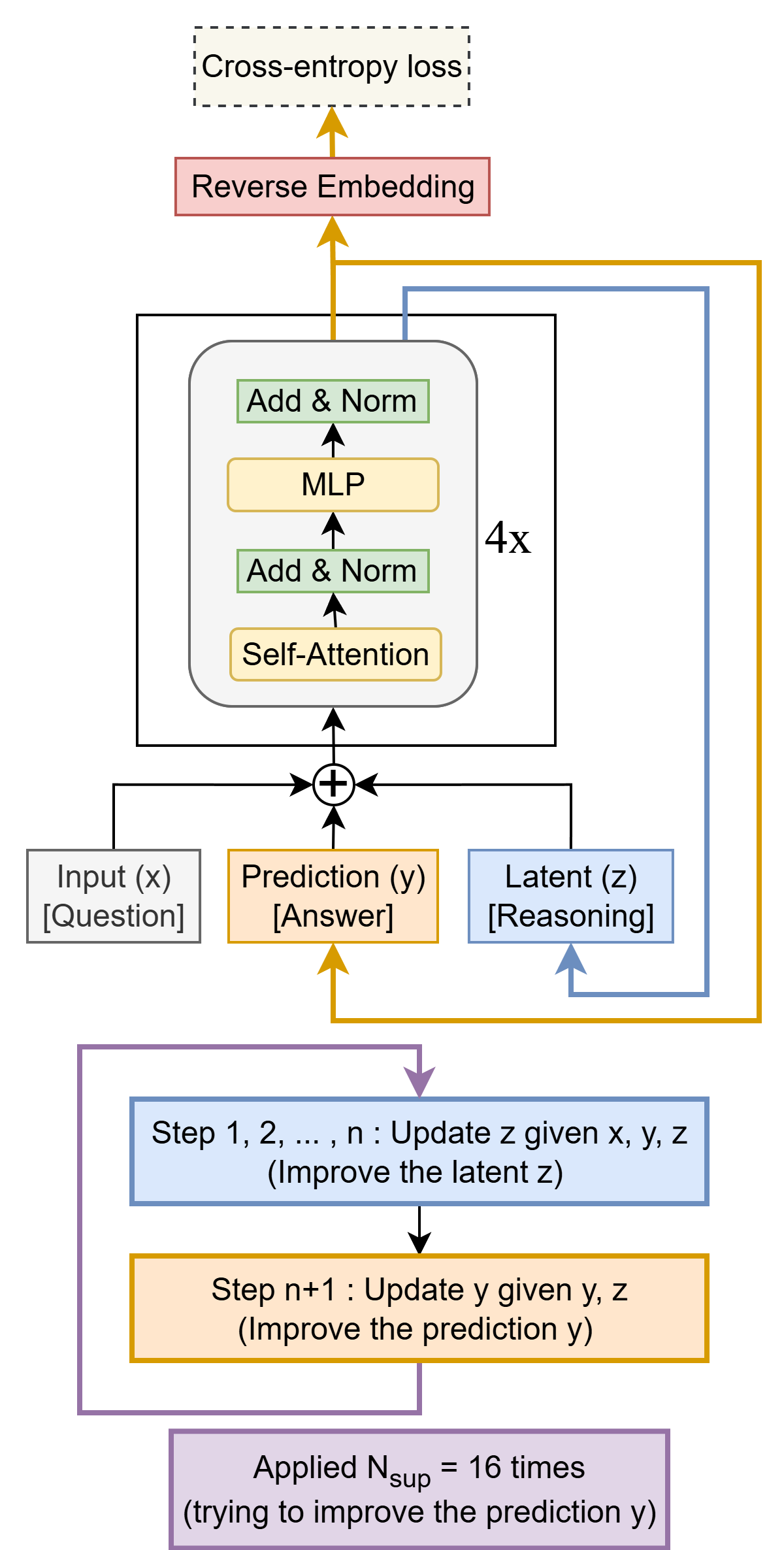
Here are the pieces inside TRM:
- Input question: the puzzle it needs to solve (like a grid for Sudoku).
- Current answer (y): its working guess for the solution.
- Hidden notes (z): like a scratchpad or memory of how it’s thinking.
The process:
- Start with the puzzle and a simple initial guess.
- Update the hidden notes (z) based on the puzzle and the current answer. This is like thinking through the puzzle again and writing better notes.
- Use those improved notes to update the answer (y). This is like revising your draft.
- Repeat steps 2–3 a few times. Each round makes the answer more accurate.
Training tricks that help:
- Deep supervision: during training, the model practices improving its answer over multiple steps, not just once. This teaches it to get better with iteration.
- Halting (early stopping): the model learns when it has likely reached the correct answer so it can stop early and save time.
- EMA (Exponential Moving Average): a stability trick that helps the model avoid overfitting on tiny datasets (think: smoothing its learning so it doesn’t jump around too much).
- Attention vs. MLP: for small, fixed-size grids (like 9×9 Sudoku), a simpler layer works better than attention. For bigger grids (like 30×30 mazes and ARC-AGI), attention works better.
What’s different from older methods (HRM)?
- HRM used two networks that ran at different speeds and relied on more complicated math assumptions. TRM uses one tiny network and trains through the full set of steps directly, which is simpler and works better.
Main findings and why they matter
The authors tested TRM on several puzzle benchmarks and compared it to HRM (the previous best small-model approach) and to big LLMs. TRM is tiny but very strong.
Key results:
- Sudoku-Extreme (very hard Sudoku, small training set): TRM reached around 87% test accuracy vs. HRM’s 55%.
- Maze-Hard (30×30 mazes): TRM reached about 85% vs. HRM’s 75%.
- ARC-AGI-1: TRM reached about 45% vs. HRM’s 40%; better than many popular LLMs.
- ARC-AGI-2: TRM reached about 8% vs. HRM’s 5%; higher than most LLMs tested.
Why this matters:
- Small models can beat big models on certain reasoning tasks if they improve their answers in steps.
- This is good news for doing more with less—lower cost, less data, and simpler training, while still getting great performance.
What’s the impact?
- More efficient AI: You don’t always need huge models and massive data to solve hard problems. Small, step-by-step reasoning can work extremely well.
- Practical for limited resources: TRM’s tiny size makes it easier to train and deploy on regular hardware.
- Clearer design: TRM avoids complicated math assumptions and complex “brain-inspired” setups. It shows that a simple loop—guess, think, improve—can be enough.
- Future directions: TRM is currently a “single-answer” system. Expanding it to generate multiple valid solutions (when puzzles allow more than one) could be a big next step. Also, understanding exactly why small-and-recursive beats big-and-flat in these cases could guide better model design across AI.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, focused list of unresolved issues that future work could address to strengthen, generalize, and better understand the proposed Tiny Recursion Model (TRM) and its comparisons to HRM and LLMs.
- Lack of theory for why recursion improves generalization: No formal explanation of why deep recursion with small networks outperforms deeper single-pass networks; derive hypotheses (e.g., implicit regularization, optimization dynamics) and validate via controlled experiments and theory (e.g., generalization bounds, bias–variance analysis).
- Stability and convergence of recursive dynamics: No guarantees or analysis of when TRM’s recursion is stable (contractive) and convergent; characterize conditions under which latent updates avoid cycles or divergence and quantify residuals across steps.
- Gradient behavior through long recursions: Unexplored risks of exploding/vanishing gradients when backpropagating through full recursion processes; paper gradient norms, stepwise Jacobians, and introduce stabilization techniques (checkpointing, reversible layers, norm constraints).
- ACT use at test time: Halting is used only in training, not at inference; evaluate learned halting at test time to trade off speed vs accuracy and paper calibration of the halting probability under distribution shift.
- ACT objective design: The simplified BCE-based halting removes the “continue” loss and the second forward pass; quantify its impact versus Q-learning ACT across tasks and compute budgets, and analyze calibration/thresholding for early stopping.
- Sensitivity to data augmentation: Performance heavily relies on extensive augmentation; systematically ablate augmentation quantity and types, assess overfitting/shortcut risks, and measure robustness when augmentations are reduced or varied.
- Puzzle-specific embeddings on ARC-AGI: The use of per-puzzle embeddings during training and testing can enable task memorization; evaluate performance without puzzle-specific identifiers and test transfer to unseen tasks or out-of-distribution puzzles.
- Voting over augmentations at test time: Accuracy is reported from selecting the most common answer across 1000 augmented runs; isolate the contribution of voting (TTC) by reporting performance without test-time augmentation and measure gains per additional augmentation.
- Comparability and fairness of baselines: Training budgets (epochs, augmentations, compute) differ across TRM, HRM, and LLM baselines; provide matched-compute comparisons and standardized protocols, including multiple random seeds and confidence intervals.
- Error taxonomy and failure modes: No analysis of where TRM fails (by puzzle types, transformation invariances, reasoning primitives); build a systematic error taxonomy to guide targeted architectural or training improvements.
- Robustness and distribution shift: Evaluate TRM under noisy inputs, occlusions, adversarial perturbations, and shifts in grid sizes/colors to verify resilience beyond curated benchmarks.
- Generalization to variable-length or large-context tasks: TRM’s attention-free variant works for small fixed grids (Sudoku) but underperforms on 30×30 grids; explore architectural changes for variable-length contexts and long-range dependencies.
- Scaling laws and compute–data trade-offs: No principled scaling laws guiding choice of parameters, recursion steps (n, T), and layers under different data regimes; establish compute-optimal configurations and learning curves across data sizes.
- Memory constraints and OOM: Full backpropagation through deep recursion leads to OOM for larger n and T; investigate memory-saving techniques (gradient checkpointing, reversible networks, truncated BPTT variants) and their effect on accuracy.
- Ratio of latent vs answer updates: TRM refines z multiple times per recursion and updates y less frequently; quantify how different update ratios affect convergence, accuracy, and training stability across tasks.
- Hyperparameter sensitivity: Limited exploration of sensitivity to n, T, EMA decay, learning rates, weight decay, and batch size; provide systematic sweeps and guidelines for robust configuration across datasets.
- Two-feature sufficiency claim: The “y and z” interpretation is compelling but supported by limited ablations on Sudoku; test whether multi-latent variants help on hierarchical or multi-stage reasoning tasks (e.g., ARC subtypes that need intermediate abstractions).
- EMA’s role and side effects: EMA improved stability/generalization, but mechanism and optimal decay rates are unexplored; analyze how EMA interacts with recursion, gradients, and overfitting across datasets.
- Loss functions and supervision signals: Use of stable-max loss and BCE on exact equality may be brittle where multiple valid solutions exist (ARC); explore alternative objectives (soft matching, structured losses, differentiable grid metrics).
- Deterministic single-answer limitation: TRM is a supervised deterministic predictor; develop a generative or probabilistic extension to represent multiple valid outputs and quantify uncertainty over candidate solutions.
- Interpretability of latent reasoning: The paper reinterprets z as latent reasoning but provides no tools to inspect or validate it; develop methods to visualize z across steps, measure monotonicity of improvement, and relate z to human-understandable reasoning traces.
- Transfer to non-grid tasks: No evidence TRM generalizes to textual, symbolic, or programmatic reasoning beyond grids; test TRM on math word problems, logic tasks, and combinatorial optimization to assess domain generality.
- Integration with LLMs and hybrid systems: Unexplored potential of combining TRM with LLMs (e.g., LLM-generated hints guiding z updates, or TRM as a verifier/solver module); design and evaluate hybrid pipelines.
- Training efficiency and sample efficiency: Despite “small data,” training runs use very many epochs; quantify sample efficiency with learning curves, early-stopping policies, and data-use efficiency compared to HRM and standard supervised baselines.
- Statistical reliability: Results lack error bars, seed variability, and significance testing; report means and standard deviations over multiple runs to assess stability and reproducibility.
Practical Applications
Immediate Applications
Below are specific, deployable use cases that can be built now with the paper’s Tiny Recursive Model (TRM) recipe (single tiny network with recursive improvement, deep supervision, halting head without extra pass, EMA, and heavy augmentation). Each item lists the sector(s), a potential tool/product/workflow, and key assumptions/dependencies.
- On-device puzzle solving and tutoring
- Sectors: consumer software, education
- Product/workflow: “TRM-Puzzles” mobile SDK to solve/give hints for Sudoku, Nonograms, Kakuro, mazes entirely offline on low-power devices; step-limited recursion and calibrated halting for snappy UX
- Assumptions/dependencies: tasks map cleanly to fixed-size grids (MLP mixer works best when L ≤ D); labeled examples or high-quality synthetic generators; augmentation (dihedral, color) to generalize
- Local path planning for small robots and toys (grid-based)
- Sectors: robotics, consumer electronics, warehousing (prototype)
- Product/workflow: “TRM-Route” module that iteratively repairs/shortens a path on discretized floor plans (30×30 attention variant); used to correct or validate A* outputs
- Assumptions/dependencies: grid discretization is acceptable; safety guardrails still rely on classical planners; domain-specific augmentations simulate obstacles/rotations
- Constraint satisfaction for configuration UIs and CPQ (small scope)
- Sectors: software, retail tech
- Product/workflow: “TRM-ConfigRepair” microservice that converts invalid UI configurations into valid ones; iterative repair loop invoked on form submit
- Assumptions/dependencies: constraints expressible on fixed-size discrete state; small curated training set + synthetic invalid/valid pairs; deterministic ground-truth exists
- Spreadsheet/CSV structure repair and validation
- Sectors: software, finance operations
- Product/workflow: “TRM-GridFix” plugin that turns invalid grids (missing totals, misaligned columns) into valid ones; runs locally and suggests minimal fixes
- Assumptions/dependencies: represent cell states and constraints in a bounded grid; high-quality labeled or programmatically generated correction pairs
- Small-scale scheduling and timetabling pilots (single ward/shift block)
- Sectors: healthcare, manufacturing (prototype scale)
- Product/workflow: “TRM-Schedule” pilot that repairs near-feasible schedules (e.g., shift swaps, lunch breaks) on compact grids; acts as post-processor to rule-based engines
- Assumptions/dependencies: scope limited to small instances; constraints codified discretely; easy-to-generate synthetic training examples with known feasible solutions
- Lightweight verification-and-repair for structured outputs
- Sectors: software engineering, MLops
- Product/workflow: “TRM-Repair” callable from apps/LLMs to validate and incrementally fix JSON schemas, matrix-like tensors, game boards; halting head used to cap compute
- Assumptions/dependencies: output can be checked for validity; a canonical corrected target exists; training data derived by corrupting valid examples
- Energy- and cost-efficient research baselines for reasoning
- Sectors: academia
- Product/workflow: Reproducible TRM baselines for ARC-AGI style tasks using 1–4 commodity GPUs; course labs on recursion vs depth, overfitting vs capacity
- Assumptions/dependencies: access to augmentation pipelines; careful selection of T and n to avoid OOM; EMA/stable-max loss to prevent divergence
- Public-sector demos of energy-efficient AI reasoning
- Sectors: policy, public sector IT
- Product/workflow: Benchmark kits showing answer-per-joule metrics on puzzles and grid planning; procurement pilots that prefer tiny, on-device reasoning
- Assumptions/dependencies: agreed-upon reporting (test-time compute, accuracy-at-budget); reproducible baselines
Long-Term Applications
The following are promising but require further research, scaling, or productization (e.g., variable-size inputs, larger contexts, safety verification, or generative extensions).
- Industrial-scale scheduling and routing
- Sectors: manufacturing, logistics
- Product/workflow: TRM++ as an iterative repair engine for job-shop/vehicle routing integrated with classical optimizers; warm-start from heuristics, then recursive improvement
- Assumptions/dependencies: variable-size support, attention scaling, domain safety constraints, rigorous benchmarking versus OR baselines
- Hospital-wide rostering and OR scheduling
- Sectors: healthcare
- Product/workflow: TRM-assisted post-processor that enforces complex constraints (skills, legal limits) with human-in-the-loop acceptance
- Assumptions/dependencies: regulatory/safety validation, explainability of repairs, robust handling of multiple valid solutions
- Discrete energy scheduling (microgrids, unit commitment prototypes)
- Sectors: energy
- Product/workflow: TRM-based local scheduler for small microgrids (battery/solar/genset on discrete time grids), later scaled to multi-asset plants
- Assumptions/dependencies: accurate simulators to synthesize training pairs; strong generalization under demand/weather shifts; integration with safety constraints
- EDA and PCB routing local improvements
- Sectors: semiconductors, CAD/EDA
- Product/workflow: TRM as a fast local router/fixer for congestion or DRC violations on discretized layouts; iterative repair in the place-and-route loop
- Assumptions/dependencies: large contexts and heterogeneous grids; co-design with existing EDA tools; high-stakes correctness guarantees
- Program repair on discrete representations (AST/CFG grids)
- Sectors: software engineering
- Product/workflow: TRM-driven iterative code fixers trained on synthetic bug/patch corpora; complements LLM codegen with deterministic repair passes
- Assumptions/dependencies: robust graph-to-grid encodings; multiple-valid-solution handling; extensive evaluation on real repositories
- Document layout and UI auto-layout correction
- Sectors: software, publishing
- Product/workflow: TRM that repairs overlaps/constraints in complex layouts, teaming with layout engines as a post-processor
- Assumptions/dependencies: large, varying grids; learnable constraint encodings; edge cases around typography and platform-specific rules
- Multi-agent/AV local planners with safety envelopes
- Sectors: robotics, transportation
- Product/workflow: TRM provides fast, local trajectory repair on occupancy grids; classical safety filters and cost maps supervise/verify
- Assumptions/dependencies: real-time constraints, robust adversarial edge-case handling, certified safety envelopes
- Finance: discrete order execution and lot-sizing heuristics
- Sectors: finance
- Product/workflow: TRM that adjusts discrete execution slices under constraints (min lot sizes, venue caps) as a post-processor to model-based policies
- Assumptions/dependencies: market non-stationarity, risk/regulatory constraints, strong backtesting and stress testing
- Generative TRMs for multi-solution problems
- Sectors: core ML, broad industry
- Product/workflow: Stochastic halting/sampling to produce diverse valid solutions; ensembles over augmentations; uncertainty-aware repair
- Assumptions/dependencies: loss design for diversity, calibration of halting head, evaluation protocols for multiple-correct outputs
- Variable-size and multimodal extensions
- Sectors: ML infrastructure, vision
- Product/workflow: Attention-based TRM that scales beyond 30×30; hybrid encoders for images/maps feeding the recursive repair core
- Assumptions/dependencies: memory-efficient attention or sparse operators; curriculum training; careful choice of T and n to avoid OOM
- LLM+TRM hybrid reasoning stacks
- Sectors: software, ML platforms
- Product/workflow: LLM delegates discrete, verifiable subproblems (routing, grid edits, schema validation) to TRM; TRM returns corrected artifacts
- Assumptions/dependencies: robust task decomposition; standardized interfaces; latency/QoS budgets and escalation to classical solvers
- Standard-setting for efficiency and compute transparency
- Sectors: policy, standards bodies
- Product/workflow: Benchmarks and reporting norms that include test-time compute/energy per correct answer; preferred procurement for energy-frugal models
- Assumptions/dependencies: multi-stakeholder coordination, reliable metrology, carrot-and-stick incentives
Common tooling and workflows that may emerge
- TRM-SDK (PyTorch) with ready-made components: augmentation ops (dihedral/color), halting head, EMA, stable-max loss, attention/MLP variants, and recipes for T/n selection based on context length and memory.
- “Recursive Repair” workflow template: initial solution (heuristic or naïve) → T−1 gradient-free improvement cycles → final gradient step (train-time) → halting-based early stop (inference) → optional majority vote over augmentations.
- Data generation kits: domain-specific synthetic pair generators (valid solution → corruptions) to create rich supervised corpora for constraint satisfaction tasks.
Global assumptions and dependencies affecting feasibility
- Tasks must be expressible as discrete, structured outputs with clear validity checks; TRM produces a single deterministic answer unless extended to generative settings.
- Performance benefits are strongest with small datasets plus heavy augmentation; overcapacity harms generalization (2-layer tiny models proved best in paper settings).
- Attention-free variant excels on small, fixed grids; attention is recommended for larger contexts (e.g., 30×30) or variable-size inputs.
- Memory grows with recursion depth n; T and n require tuning to balance accuracy, latency, and OOM risk; EMA and stability-focused losses are important for small-data regimes.
- Safety-critical deployments must pair TRM with rule-based verifiers or certified planners; human-in-the-loop review advisable for high-stakes domains.
Glossary
- 1-step gradient approximation: Technique that approximates gradients at an equilibrium by backpropagating only the final iteration(s) of a recursion. "the Implicit Function Theorem \citep{krantz2002implicit} with the 1-step gradient approximation \citep{bai2019deep} is used to approximate the gradient by back-propagating only the last and steps."
- Adaptive computational time (ACT): A learned halting mechanism that decides when to stop iterating on a sample during training to balance compute and data coverage. "HRM uses Adaptive computational time (ACT) during training to optimize the time spent of each data sample."
- ARC-AGI: A benchmark of human-intuitive pattern reasoning tasks (with ARC-AGI-1 and ARC-AGI-2 variants) designed to be hard for current AI systems. "While LLMs have made significant progress on ARC-AGI \citep{chollet2019measure} since 2019, human-level accuracy still has not been reached"
- Backpropagation Through Time (BPTT): Training method for recurrent models that unrolls computations across timesteps to propagate gradients. "Deep supervision and the 1-step gradient approximation provide a more biologically plausible and less computationally-expansive alternative to Backpropagation Through Time (BPTT) \citep{werbos1974beyond, rumelhart1985learning, lecun1985procedure} for solving the temporal credit assignment (TCA) \citep{rumelhart1985learning, werbos1988generalization, elman1990finding} problem \citep{lillicrap2019backpropagation}."
- Chain-of-thoughts (CoT): Prompting strategy that elicits step-by-step intermediate reasoning before producing the final answer. "LLMs rely on Chain-of-thoughts (CoT) \citep{wei2022chain}"
- Deep equilibrium models: Architectures that define outputs via fixed points of implicit layers, often trained using implicit differentiation. "Deep equilibrium models normally do fixed-point iteration to solve for the fixed point \citep{bai2019deep}."
- Deep supervision: Training scheme where intermediate iterative steps are supervised to improve effective depth and iterative refinement. "Deep supervision consists of improving the answer through multiple supervision steps while carrying the two latent features as initialization for the improvement steps (after detaching them from the computational graph so that their gradients do not propagate)."
- Exponential Moving Average (EMA): A running average of model parameters used to stabilize training and improve generalization. "To reduce this problem and improves stability, we integrate Exponential Moving Average (EMA) of the weights, a common technique in GANs and diffusion models \citep{brock2018large, song2020improved}."
- Fixed-point iteration: Procedure that repeatedly applies a function to approach a point where the input equals the output. "Deep equilibrium models normally do fixed-point iteration to solve for the fixed point \citep{bai2019deep}."
- Hierarchical Reasoning Model (HRM): A supervised model that uses two recurrent networks operating at different frequencies with deep supervision to iteratively refine answers. "Hierarchical Reasoning Model (HRM) is a novel approach using two small neural networks recursing at different frequencies."
- Implicit Function Theorem (IFT): Mathematical theorem enabling differentiation of implicitly defined functions, used here to justify gradient approximations at fixed points. "the Implicit Function Theorem \citep{krantz2002implicit} with the 1-step gradient approximation \citep{bai2019deep} is used to approximate the gradient"
- Mixture-of-Experts (MoE): Sparse neural architecture that routes inputs to different expert subnetworks to increase capacity efficiently. "We tried replacing the SwiGLU MLPs by SwiGLU Mixture-of-Experts (MoEs) \citep{shazeer2017outrageously, fedus2022switch}, but we found generalization to decrease massively."
- MLP-Mixer: Model architecture that mixes token and channel dimensions using only MLPs, removing attention. "Taking inspiration from the MLP-Mixer \citep{tolstikhin2021mlp}, we can replace the self-attention layer with a multilayer perceptron (MLP) applied on the sequence length."
- Q-learning: Reinforcement learning algorithm that learns action-value functions to guide decisions, used here to learn halting. "It is learned through a Q-learning objective that requires passing the through an additional head and running an additional forward pass (to determine if halting now rather than later would have been preferable)."
- RMSNorm: Normalization technique that scales activations by their root-mean-square without centering. "Each network is a 4-layer Transformers architecture \citep{vaswani2017attention}, with RMSNorm \citep{zhang2019root}, no bias \citep{chowdhery2023palm}, rotary embeddings \citep{su2024roformer}, and SwiGLU activation function \citep{hendrycks2016gaussian, shazeer2020glu}."
- Rotary embeddings: Positional encoding method that injects relative position information via rotations in attention. "Each network is a 4-layer Transformers architecture \citep{vaswani2017attention}, with RMSNorm \citep{zhang2019root}, no bias \citep{chowdhery2023palm}, rotary embeddings \citep{su2024roformer}, and SwiGLU activation function \citep{hendrycks2016gaussian, shazeer2020glu}."
- Self-attention: Mechanism that computes dependencies between all token pairs via attention weights. "Using an MLP instead of self-attention, we obtain better generalization on Sudoku-Extreme (improving from 74.7\% to 87.4\%; see Table \ref{tab:ablation})."
- Stable-max loss: A loss variant designed to improve optimization stability compared to standard softmax cross-entropy. "and stable-max loss \citep{prieto2025grokking} for improved stability."
- SwiGLU: Gated activation function combining Swish and GLU for improved expressivity. "Each network is a 4-layer Transformers architecture \citep{vaswani2017attention}, with RMSNorm \citep{zhang2019root}, no bias \citep{chowdhery2023palm}, rotary embeddings \citep{su2024roformer}, and SwiGLU activation function \citep{hendrycks2016gaussian, shazeer2020glu}."
- Temporal credit assignment (TCA): The problem of determining which past computations or states are responsible for current performance. "Deep supervision and the 1-step gradient approximation provide a more biologically plausible and less computationally-expansive alternative to Backpropagation Through Time (BPTT) \citep{werbos1974beyond, rumelhart1985learning, lecun1985procedure} for solving the temporal credit assignment (TCA) \citep{rumelhart1985learning, werbos1988generalization, elman1990finding} problem \citep{lillicrap2019backpropagation}."
- Test-Time Compute (TTC): Strategy of allocating extra inference-time computation (e.g., sampling multiple answers) to improve accuracy. "To improve their reliability, LLMs rely on Chain-of-thoughts (CoT) \citep{wei2022chain} and Test-Time Compute (TTC) \citep{snell2024scaling}."
- Tiny Recursive Model (TRM): The proposed single-network recursive reasoning approach that iteratively refines latent state and answer. "We propose Tiny Recursive Model (TRM), a much simpler recursive reasoning approach that achieves significantly higher generalization than HRM, while using a single tiny network with only 2 layers."
- TorchDEQ: A PyTorch library for Deep Equilibrium Models providing fixed-point solvers and implicit differentiation tools. "We tried using TorchDEQ \citep{geng2023torchdeq} to replace the recursion steps by fixed-point iteration as done by Deep Equilibrium Models \citep{bai2019deep}."
Collections
Sign up for free to add this paper to one or more collections.