Mixture-of-Recursions: Learning Dynamic Recursive Depths for Adaptive Token-Level Computation (2507.10524v2)

Abstract: Scaling LLMs unlocks impressive capabilities, but the accompanying computational and memory demands make both training and deployment expensive. Existing efficiency efforts typically target either parameter sharing or adaptive computation, leaving open the question of how to attain both simultaneously. We introduce Mixture-of-Recursions (MoR), a unified framework that combines the two axes of efficiency inside a single Recursive Transformer. MoR reuses a shared stack of layers across recursion steps to achieve parameter efficiency, while lightweight routers enable adaptive token-level thinking by dynamically assigning different recursion depths to individual tokens. This allows MoR to focus quadratic attention computation only among tokens still active at a given recursion depth, further improving memory access efficiency by selectively caching only their key-value pairs. Beyond these core mechanisms, we also propose a KV sharing variant that reuses KV pairs from the first recursion, specifically designed to decrease prefill latency and memory footprint. Across model scales ranging from 135M to 1.7B parameters, MoR forms a new Pareto frontier: at equal training FLOPs and smaller model sizes, it significantly lowers validation perplexity and improves few-shot accuracy, while delivering higher throughput compared with vanilla and existing recursive baselines. These gains demonstrate that MoR is an effective path towards large-model quality without incurring large-model cost.

• The paper presents adaptive token-level recursion where lightweight routers assign dynamic recursion depths for each token.
• It reduces FLOPs and memory usage while achieving lower validation loss and improved few-shot accuracy compared to baselines.
• Experiments across varying model sizes demonstrate significant inference speedups and scalable, compute-optimal performance.

Mixture-of-Recursions: Adaptive Token-Level Computation through Dynamic Recursive Depths

The paper "Mixture-of-Recursions: Learning Dynamic Recursive Depths for Adaptive Token-Level Computation" (2507.10524) introduces Mixture-of-Recursions (MoR), a framework that unifies parameter sharing and adaptive computation within Recursive Transformers. By training lightweight routers to assign token-specific recursion depths, MoR directs computation to where it is most needed, reducing both FLOPs and memory traffic. The paper demonstrates that MoR achieves a new Pareto frontier, improving validation loss, few-shot accuracy, and inference throughput compared to vanilla and recursive baselines across various model scales.

Architectural Overview

MoR builds upon the Recursive Transformer architecture, which reuses a shared stack of layers across multiple recursion steps (Figure 1). This parameter sharing reduces the model's memory footprint. The core innovation of MoR lies in its ability to dynamically adjust the recursion depth for each token, allowing the model to focus computation on more complex tokens. This is achieved through lightweight routers trained end-to-end to assign token-specific recursion depths.

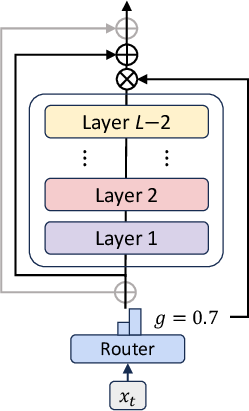
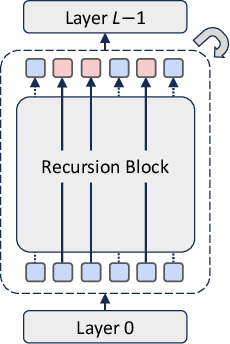
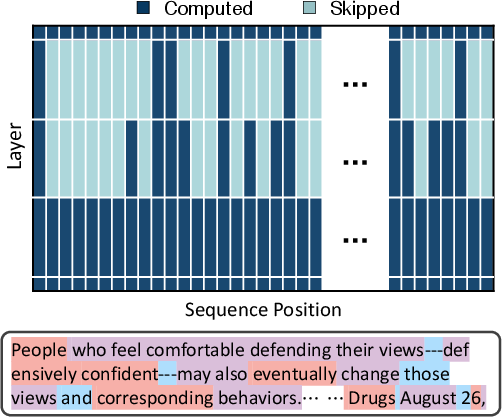
Figure 1: Overview of the Mixture-of-Recursions (MoR) framework, illustrating the shared recursion block, the overall model structure, and an example routing pattern showcasing token-wise recursion depth.

The routers determine how many times a shared parameter block is applied to each token based on its required depth of "thinking." This dynamic, token-level recursion facilitates recursion-wise key-value (KV) caching, selectively storing and retrieving KV pairs corresponding to each token’s assigned recursion depth.

Routing Strategies

The paper explores two routing strategies: expert-choice and token-choice (Figure 2).

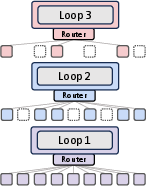
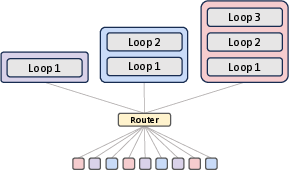
Figure 2: Architectural components of the Mixture-of-Recursions (MoR), depicting expert-choice routing, token-choice routing, and KV caching strategies.

In expert-choice routing, each recursion depth acts as an expert, selecting the top-$k$ tokens to continue to the next recursion step. This progressive narrowing of active tokens with depth allows deeper layers to focus on more abstract and sparse information. In token-choice routing, each token is assigned a fixed recursion depth at the outset via a single routing decision. This commits each token to a full sequence of recursion blocks from the start. The paper aligns the token allocation budgets of expert-choice with that of token-choice to compare routing strategies under equal compute. While expert-choice routing guarantees perfect load balancing with static top-$k$ selection, it suffers from information leakage. Token-choice is free from such leakage but typically requires a balancing loss due to its inherent load balancing challenges.

KV Caching Strategies

To address KV cache consistency during autoregressive decoding, the paper designs and explores two KV cache strategies tailored to MoR models: recursion-wise caching and recursive sharing. In recursion-wise caching, only tokens routed to a given recursion step store their key-value entries at that level. Attention is then restricted to those locally cached tokens. This design promotes block-local computation, improving memory efficiency and reducing IO demands. In recursive KV sharing, KV pairs are cached exclusively at the initial recursion step and reused across all subsequent recursions. This ensures all tokens can access past context without recomputation, despite any distribution mismatch.

Experimental Results

The paper pretrains models from scratch using a Llama-based Transformer architecture on a deduplicated subset of the FineWeb-Edu dataset. The models are evaluated on the validation set of FineWeb-edu and six few-shot benchmarks. The results demonstrate that MoR outperforms baselines with fewer parameters under equal training compute. Under an equal training budget of 16.5e18 FLOPs, the MoR model achieves a lower validation loss and surpasses the vanilla baseline in average few-shot accuracy (43.1% vs. 42.3%), despite using nearly 50% fewer parameters.

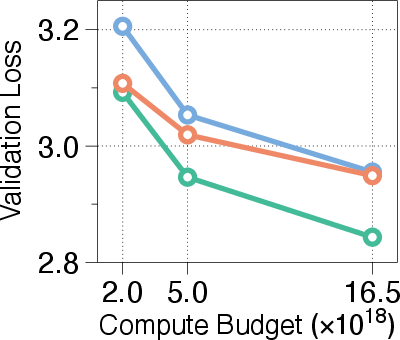
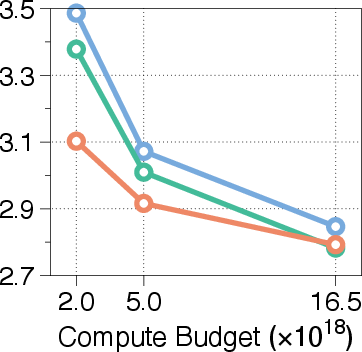
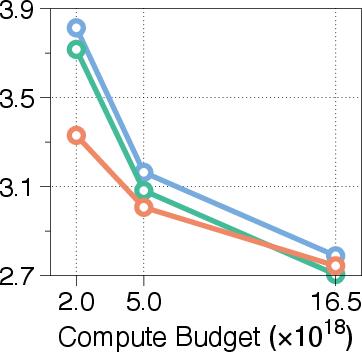
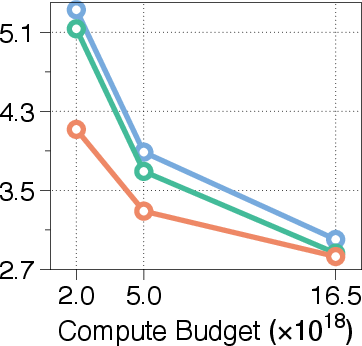
Figure 3: Validation loss across different compute budgets and model sizes, showcasing MoR's consistent outperformance of recursive baselines and competitive performance with standard Transformers.

The paper also analyzes performance under a fixed number of training tokens (20B). The MoR model with $N_r=2$ outperforms both vanilla and recursive baselines, achieving lower validation loss and higher accuracy, despite using 25% fewer training FLOPs. These theoretical efficiencies translate into significant practical gains: compared to the vanilla baseline, the model reduces training time by 19% and cuts peak memory usage by 25%.

Inference Throughput Evaluation

As a parameter-shared architecture, MoR can leverage continuous depth-wise batching to dramatically boost inference throughput compared to Vanilla Transformers. The early-exiting mechanism in MoR further eliminates bubbles in the computational batch. In \autoref{fig:pareto_frontier_sharing-a}, across both batch settings, all MoR variants outperform the vanilla baseline, which even leverages continuous sequence-wise batching. Increasing recursion depth leads to more tokens exiting early and a further reduction in KV cache usage, boosting throughput significantly.

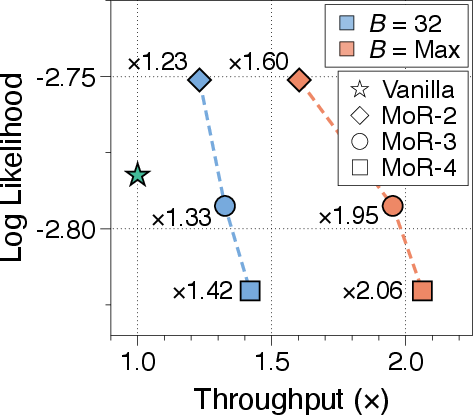
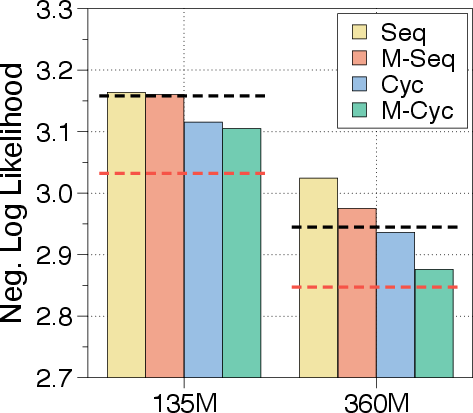
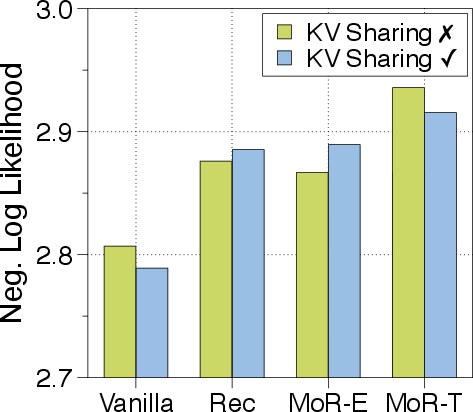
Figure 4: Pareto frontier of inference throughput and log-likelihood for MoR and Vanilla Transformer under fixed and maximum batching scenarios.

For example, MoR with four recursions achieves up to a 2.06$\times$ speedup.

Compute-Optimal Scaling Analysis

The paper evaluates MoR against both Vanilla and Recursive Transformers across a wide range of model sizes and computational budgets. As shown in \autoref{fig:scaling_laws_app}, MoR consistently outperforms recursive baselines across all model sizes and compute budgets. For >360M parameters, MoR not only matches but often exceeds the Vanilla Transformer, particularly under low and mid-range budgets. These results highlight that MoR is a scalable and efficient alternative to standard Transformers.

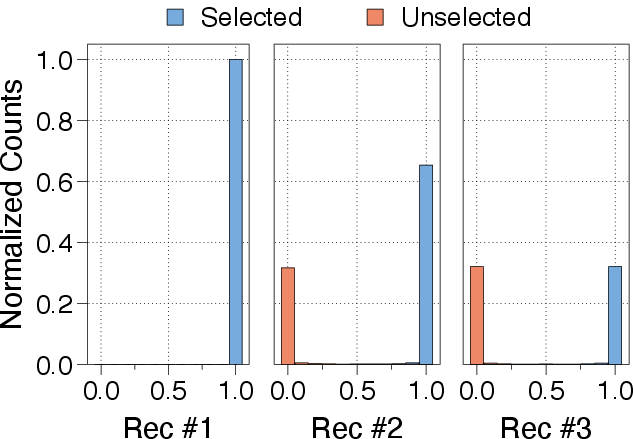
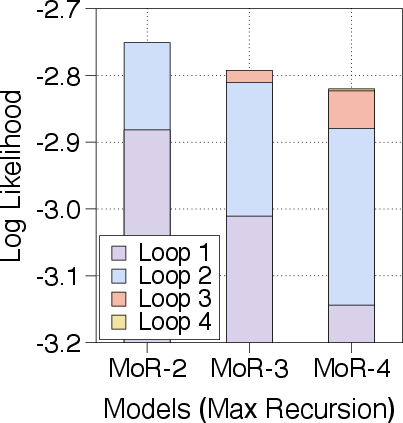
Figure 5: Compute-optimal scaling analysis for three model architectures, demonstrating that MoR's scaling favors model size over training length under isoFLOPs constraints.

As illustrated in \autoref{fig:isoflops_qualitative-a}, MoR exhibits a distinct compute-optimal scaling behavior compared to baselines under isoFLOPs constraints. The flatter slope of MoR's optimal path indicates that it benefits more significantly from increases in parameter count (i.e., less data-hungry). Therefore, the optimal scaling policy for MoR models favors allocating resources to increasing model capacity by using larger models trained for shorter steps.

Conclusion

The paper "Mixture-of-Recursions: Learning Dynamic Recursive Depths for Adaptive Token-Level Computation" (2507.10524) presents a unified Transformer architecture that simultaneously leverages parameter sharing, adaptive recursion depth, and efficient KV caching without compromising model quality. By dynamically assigning recursion depth to tokens via lightweight routers and selectively caching key-value states for selected tokens, MoR reduces both quadratic attention computation and redundant memory access costs. The results demonstrate that MoR offers an effective path towards achieving large-model capabilities with significantly reduced computational and memory overhead.