A Euclidean likelihood estimator for bivariate tail dependence

Abstract: The spectral measure plays a key role in the statistical modeling of multivariate extremes. Estimation of the spectral measure is a complex issue, given the need to obey a certain moment condition. We propose a Euclidean likelihood-based estimator for the spectral measure which is simple and explicitly defined, with its expression being free of Lagrange multipliers. Our estimator is shown to have the same limit distribution as the maximum empirical likelihood estimator of J. H. J. Einmahl and J. Segers, Annals of Statistics 37(5B), 2953--2989 (2009). Numerical experiments suggest an overall good performance and identical behavior to the maximum empirical likelihood estimator. We illustrate the method in an extreme temperature data analysis.

• The paper introduces a Euclidean likelihood estimator that explicitly computes the spectral measure under moment constraints in bivariate extremes.
• It proves the estimator’s asymptotic equivalence to empirical likelihood methods while simplifying computation by avoiding Lagrange multipliers.
• Monte Carlo experiments and environmental applications validate the method’s improved efficiency in capturing extremal dependence, using metrics like mean integrated squared error.

A Euclidean Likelihood Estimator for Bivariate Tail Dependence

Introduction

The statistical characterization and estimation of extremal dependence in bivariate settings is inherently constrained by the necessity to correctly capture the asymptotic structure, particularly as encoded by the spectral measure. This measure, central in the representation of bivariate extreme value distributions, determines the limiting behavior of normalized maxima and must satisfy a moment constraint induced by marginal normalization. The complexity of nonparametric inference under this constraint leads to technical and computational challenges for existing methods such as empirical and empirical likelihood estimators. The paper "A Euclidean likelihood estimator for bivariate tail dependence" (1204.3524) proposes and systematically studies a Euclidean likelihood-based estimator for the spectral measure, focusing on its theoretical properties, finite-sample performance, and application to environmental data.

Theoretical Framework

Bivariate extremes are modeled by standardizing the marginals to unit Pareto (or unit Fréchet) and examining the weak convergence of the rescaled maxima. The limiting distribution necessarily has the form

$$G(x, y) = \exp\left\{ -2 \int_{[0, 1]} \max\left(\frac{w}{x}, \frac{1-w}{y}\right) dH(w) \right\},$$

where %%%%1%%%% is the spectral measure, a probability measure on $[0,1]$ constrained by $\int_{[0,1]} w\, dH(w) = 1/2$. This measure governs the distribution of pseudo-angles $W_i = X_i^* / (X_i^* + Y_i^*)$, given large pseudo-radius $R_i = X_i^* + Y_i^*$.

Inference for $H$ is usually made from pseudo-angles corresponding to observations exceeding a high threshold. However, estimating $H$ is nontrivial due to its moment constraint and the induced dependence among pseudo-angles arising from marginal transformation.

The Maximum Euclidean Likelihood Estimator

The proposed estimator applies the Euclidean likelihood paradigm, defining the objective for probabilities $\mathbf{p} = (p_1, ..., p_k)$ at observed pseudo-angles $(w_1, ..., w_k)$ as

$$\ell_E(\mathbf{p}) = -\frac{1}{2}\sum_{i=1}^k (k p_i - 1)^2,$$

measuring the Euclidean distance to the barycenter of the probability simplex while imposing the required constraints on the weights:

$\sum_i p_i = 1, \qquad \sum_i w_i p_i = 1/2.$

The estimator is entirely explicit, obtaining $$\hat p_i = \frac{1}{k} \{ 1 - (\overline{w} - 1/2) S^{-2} (w_i - \overline{w}) \}$$, with $\overline{w}$ and $S^2$ the sample mean and variance. The absence of Lagrange multipliers simplifies computation and the subsequent analysis.

Asymptotic Properties

The estimator's asymptotic theory is developed using functional analytic tools. The mapping from the empirical spectral measure to the Euclidean likelihood estimator is shown to be continuous and Hadamard differentiable, allowing direct application of both the continuous mapping theorem and the functional delta method. The result is that the Euclidean likelihood estimator achieves the same limit distribution as the empirical likelihood estimator of Einmahl and Segers (2009), ensuring asymptotic equivalence in efficiency.

Monte Carlo Assessment

Numerical experiments focus on the bivariate logistic model for extremes, considering both moderate and strong dependence settings. The mean integrated squared error (MISE) is used to contrast the empirical spectral measure, the empirical likelihood, and the Euclidean likelihood estimators. The results reveal nearly indistinguishable trajectories for the two likelihood-based estimators, supporting the theoretical equivalence (Figure 1):

Figure 1: Trajectories of empirical, empirical likelihood, and Euclidean likelihood spectral measure estimators for logistic bivariate extremes, compared to the true $H_\alpha$.

The MISE curves (Figure 2) confirm that the likelihood-based estimators offer improved efficiency (lower MISE) over the pure empirical procedure, particularly at moderate threshold choices.

Figure 2: Logarithms of mean integrated squared errors for the spectral measure estimators across multiple Monte Carlo experiments.

A subtlety is that the Euclidean likelihood estimator can yield negative weights, though this is rare except under extreme thresholding and diminishes with weaker dependence (Figure 3).

Figure 3: Proportion of negative weights in the Euclidean likelihood estimator as a function of thresholding and dependence parameter.

Application to Environmental Extremes

An applied analysis is conducted on daily average air temperatures measured at two neighboring sites—open field and under forest cover—in Beatenberg, Switzerland, focusing on understanding their joint extremal behavior. After preprocessing (deseasonalization and thresholding), pseudo-angles are derived from daily maxima exceeding the 98% quantile for the sum of residuals.

Raw time series and thresholded (pseudo-radius) observations are illustrated in Figures 4 and 5:

Figure 4: Daily average air temperatures under forest cover and in open field (raw time series).

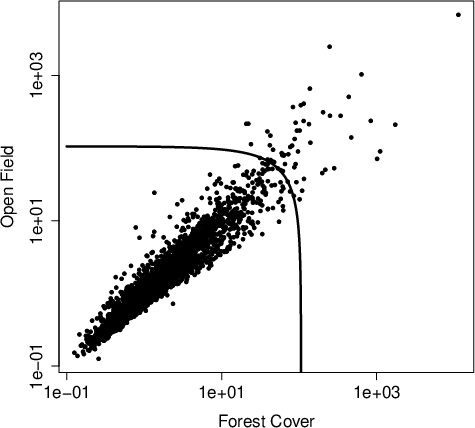
Figure 5: Scatterplot of temperature data on unit Fréchet scale with threshold boundary.

Extremal dependence assessment using empirical estimates of $\chi(u)$ and $\overline{\chi}(u)$ supports the applicability of spectral measure modeling (Figure 6).

Figure 6: Empirical estimates and confidence intervals for extremal dependence measures $\chi(u)$ and $\overline{\chi}(u)$.

The Euclidean likelihood estimator and its smoothed version (via Beta kernel convolution) provide estimates for the spectral measure and density (Figure 7), as well as for the Pickands dependence function and the joint extreme value distribution (Figure 8).

Figure 7: Empirical and smoothed (Beta kernel) Euclidean spectral measure and density for the air temperature data, with comparison to the fitted asymmetric logistic model.

Figure 8: Smoothed Pickands dependence function and level contours for the estimated bivariate extreme value distribution.

For this data, the analysis suggests notable extremal dependence with skewness in the angular measure, interpreted as evidence of the forest's capacity to retain heat under extreme conditions, an effect not sufficiently captured by parametric models.

Conclusion

The Euclidean likelihood estimator for the spectral measure in bivariate extremes offers a computationally explicit, constraint-respecting, and theoretically robust alternative to empirical and empirical likelihood estimators. The key result is that asymptotic distribution and efficiency are preserved compared to the empirical likelihood approach, while computation is simplified by avoiding Lagrange multipliers. Simulation results confirm this equivalence, and real data analysis demonstrates the utility for assessing extremal dependence in environmental settings, highlighting effects potentially missed by standard parameterizations. The framework can be generalized to other representations, such as to measures over $L_p$-norm unit spheres, and kernel smoothing techniques yield smooth functional estimates without violating essential moment conditions.

Implications: The method provides a flexible approach for semi- and nonparametric modeling of extremal dependence, crucial for accurate risk estimation in multivariate settings where parametric models may be misspecified. Extensions to $d$-variates or alternative constraint structures are direct. Future work would entail high-dimensional generalization, adaptation to censored or incomplete data, and integration with advanced model selection procedures.

Reference:

A Euclidean likelihood estimator for bivariate tail dependence (1204.3524)