Likelihood-Based Ergodicity Transformations in Time Series Analysis

Abstract: Time series often exhibit non-ergodic behaviour that complicates forecasting and inference. This article proposes a likelihood-based approach for estimating ergodicity transformations that addresses such challenges. The method is broadly compatible with standard models, including Gaussian processes, ARMA, and GARCH. A detailed simulation study using geometric and arithmetic Brownian motion demonstrates the ability of the approach to recover known ergodicity transformations. A further case study on the large macroeconomic database FRED-QD shows that incorporating ergodicity transformations can provide meaningful improvements over conventional transformations or naive specifications in applied work.

• The paper introduces a likelihood-based method for estimating transformations that restore ergodicity in non-ergodic time series.
• It employs a maximum likelihood framework on Box-Cox family transformations to minimize variance in increments, validated via GBM and ABM simulations.
• The method improves factor interpretability and forecasting performance in macroeconomic data relative to traditional transformation techniques.

Likelihood-Based Ergodicity Transformations for Time Series Analysis

Introduction and Motivation

The treatment of non-ergodic behavior in time series is a central problem across empirical domains requiring statistical inference from a single realisation, including economics, finance, and geophysics. The conventional approach in time series relies on ergodicity to guarantee that time averages of stochastic processes converge to ensemble averages, making parameter inference and forecasting feasible. Many processes encountered empirically, however, exhibit non-ergodic behavior, and standard transformations such as logarithms or Box-Cox power transformations are typically justified by variance stabilization rather than ergodicity considerations.

The present work introduces a likelihood-based method for data-driven estimation of ergodicity transformations, designed so that after transformation, the observable process admits modeling under stationary, ergodic frameworks such as Gaussian processes, ARMA, or GARCH models. This extends existing transformation approaches by focusing directly on the restoration of statistical ergodicity, which is fundamental for consistent inference and model validity.

Likelihood-Based Estimation of Ergodicity Transformations

The proposed procedure involves searching for a transformation $F(\cdot;\lambda)$, commonly chosen from the Box-Cox family, such that the increment process $\Delta F(X_t)$ is as close as possible to stationary, ergodic Gaussian noise. Understationarity and short-memory conditions, the process is ergodic for all moments, aligning time-averaged statistics with ensemble moments. For parameter estimation, maximization of the multivariate Gaussian log-likelihood is performed across the transformation parameter $\lambda$, effectively identifying the transformation that maximizes the fit to an ergodic process.

An important distinction from traditional Box-Cox methodology is that the current approach minimizes the variance of the increments of the transformed process, not simply the variance of the transformed levels. This guarantees interpretability for stochastic processes whose intrinsic growth or fluctuation properties are captured only after differencing or transformation.

Case Study: Identification of Ergodicity Transformations in Simulated SDEs

The method is first validated using simulated paths of geometric and arithmetic Brownian motions (GBM and ABM).

Ten sample trajectories of GBM and ABM exhibit the prototypical behavior (Figure 1):

Figure 1: Ten sample trajectories each of geometric and arithmetic Brownian motion with drift $\mu = 0.05$, volatility $\sigma = 0.2$, and initial condition $X_0 = 1$, over three trading years.

For GBM, the theoretically correct ergodicity transformation is $\Delta\log X_t$ (i.e., $\lambda = 0$ in the Box-Cox family), while for ABM, the identity ($\lambda = 1$) suffices. The profile log-likelihood for ergodicity transformation (right panel) is sharply peaked at the correct values for each realization, a result not achieved under standard variance-minimizing Box-Cox transformations applied to levels (left panel, Figure 2):

Figure 2: Box-Cox versus likelihood-based profile log-likelihoods for GBM, showing efficacy of the proposed approach in recovering $\lambda = 0$ for every realization.

In ABM, the ergodicity-focused likelihood similarly identifies $\lambda = 1$ for the true generative path (Figure 3):

Figure 3: As in Figure 2, but for arithmetic Brownian motion, with the ergodicity transformation peaking at $\lambda = 1$.

The accuracy and statistical uncertainty of the estimator depend on sample size and the signal-to-noise ratio (Figure 4). Bias and variance decrease appreciably at larger $T$, but identification may deteriorate if scale overwhelms the innovation process, especially for additive processes.

Figure 4: Effects of sample size on the empirical bias and variance in estimated ergodicity transformation parameter $\hat{\lambda}$.

Cross-Sectional Application: Macroeconomic Factors in FRED-QD

The method is applied to the FRED-QD macroeconomic database to re-examine conventional choices regarding stationarity and transformation in factor modeling. Estimated transformation parameters differ substantially from those implied by FRED-QD's native protocols: a considerable mass of power estimates fall in $(0,1)$, indicating a richer structure than simple log or level choices (Figure 5).

Figure 5: Estimated power transformation parameters $\lambda$ across FRED-QD series, grouped by order of integration.

Dynamic factor models are estimated under three transformation regimes – FRED-QD's own, Box-Cox, and likelihood-based ergodicity. Factor solutions are visually similar across methods (Figure 6), but systematic structural differences emerge. Notably, for higher-indexed factors, the ergodicity transformation delivers more coherent economic groupings and improved separation between macroeconomic dimensions, avoiding confounding between inflation and financial/real factors seen in conventional transformations:

Figure 6: Comparison of factors from benchmark, Box-Cox, and likelihood-based ergodicity transformations.

Direct comparison to the benchmark shows non-negligible, systematic drift and differences, especially for higher factors (Figure 7):

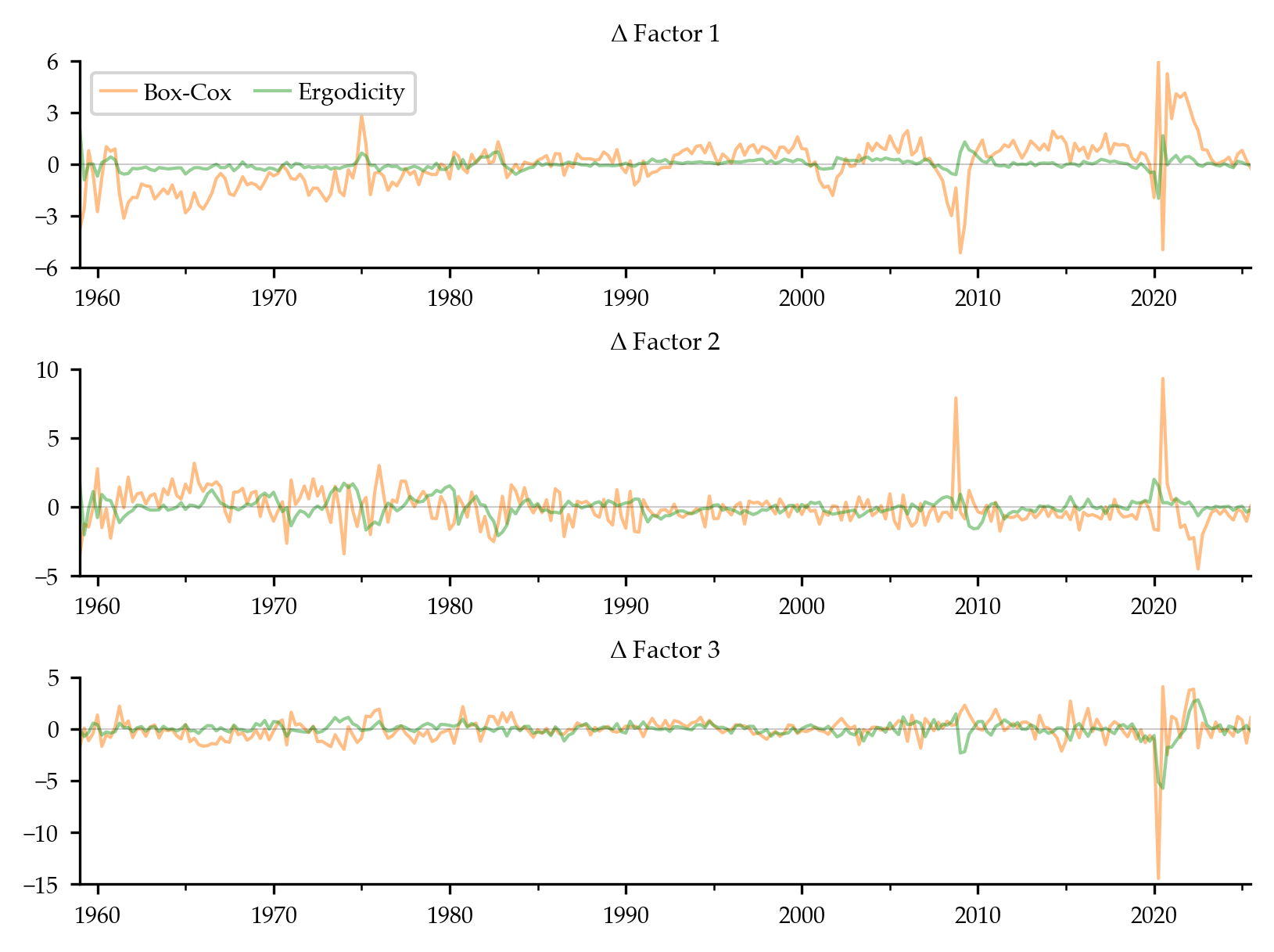
Figure 7: Differences between factors extracted using Box-Cox/ergodicity transformations and FRED-QD benchmark factors.

Forecasting Evaluation and Robustness

Forecasting performance in an expanding window exercise confirms the practical utility of the method. The ergodicity-based transformations provide robust, often superior median accuracy across economic groups, especially relative to the Box-Cox alternative, which systematically underperforms in mean and median metrics. The ergodicity approach is especially advantageous for credit and balance sheet aggregates, suggesting its capacity to respect the underlying data-generating processes of stock and flow variables.

Theoretical and Practical Implications

The identification of ergodicity transformations by likelihood enables consistent inference and statistical testing in environments where ensemble averages are inaccessible. The approach is model-agnostic, integrating seamlessly with subsequent univariate or multivariate modeling stages. Theoretical implications include a principled pathway to restoring ergodic behavior to non-ergodic empirical time series. Practically, the results carry significance for economic forecasting, financial econometrics, and anywhere robust long-horizon inference is required from a single realization.

This framework also highlights limitations of traditional transformation practices in time series analysis, particularly in the context of dynamic factor models where the choice of transformation materially impacts the economic interpretation and quality of latent factors.

Future Directions

Further research could expand on joint estimation of transformation and model parameters, including the concurrent handling of unit root and non-linear transformation hypotheses. Robustification to heavy-tailed or outlier-contaminated settings is another avenue, for instance by coupling the ergodicity-likelihood procedure with median- or quantile-based measures.

On the theoretical side, extensive study of identification strength, signal-to-noise requirements for accurate transformation inference, and extensions to long-memory or fractionally integrated processes remain.

Conclusion

The likelihood-based estimation of ergodicity transformations generalizes standard practice in time series preprocessing and enables consistent and interpretable modeling for a broad class of non-ergodic empirical processes. The technique enhances factor interpretability and forecasting performance in macroeconomic panels and provides a flexible framework for future developments in time series methodology.

Reference: "Likelihood-Based Ergodicity Transformations in Time Series Analysis" (2601.11237).