Improving Reasoning for Diffusion Language Models via Group Diffusion Policy Optimization (2510.08554v1)

Abstract: Diffusion LLMs (DLMs) enable parallel, order-agnostic generation with iterative refinement, offering a flexible alternative to autoregressive LLMs. However, adapting reinforcement learning (RL) fine-tuning to DLMs remains an open challenge because of the intractable likelihood. Pioneering work such as diffu-GRPO estimated token-level likelihoods via one-step unmasking. While computationally efficient, this approach is severely biased. A more principled foundation lies in sequence-level likelihoods, where the evidence lower bound (ELBO) serves as a surrogate. Yet, despite this clean mathematical connection, ELBO-based methods have seen limited adoption due to the prohibitive cost of likelihood evaluation. In this work, we revisit ELBO estimation and disentangle its sources of variance. This decomposition motivates reducing variance through fast, deterministic integral approximations along a few pivotal dimensions. Building on this insight, we introduce \textbf{Group Diffusion Policy Optimization (GDPO)}, a new RL algorithm tailored for DLMs. GDPO leverages simple yet effective Semi-deterministic Monte Carlo schemes to mitigate the variance explosion of ELBO estimators under vanilla double Monte Carlo sampling, yielding a provably lower-variance estimator under tight evaluation budgets. Empirically, GDPO achieves consistent gains over pretrained checkpoints and outperforms diffu-GRPO, one of the state-of-the-art baselines, on the majority of math, reasoning, and coding benchmarks.

• The paper introduces Group Diffusion Policy Optimization (GDPO) which leverages sequence-level ELBO estimates to optimize diffusion language models with reduced bias and variance.
• It employs a Semi-deterministic Monte Carlo (SDMC) estimator via Gaussian quadrature, achieving efficiency and computational gains with fewer evaluations.
• GDPO outperforms baselines on reasoning, planning, and coding tasks, offering both theoretical error bounds and empirical performance improvements.

Improving Reasoning for Diffusion LLMs via Group Diffusion Policy Optimization

Introduction and Motivation

Diffusion LLMs (DLMs) have emerged as a compelling alternative to autoregressive LLMs, offering parallel, order-agnostic generation and iterative refinement. These properties enable faster inference, flexible token revision, and improved robustness to error propagation. However, adapting reinforcement learning (RL) fine-tuning to DLMs is nontrivial due to the intractability of likelihood estimation, which is central to most RL objectives. Prior work, such as diffu-GRPO, introduced heuristic token-level likelihood approximations via one-step unmasking, achieving computational efficiency but suffering from significant bias and limited theoretical grounding.

This paper introduces Group Diffusion Policy Optimization (GDPO), a novel RL algorithm tailored for DLMs. GDPO leverages sequence-level likelihoods, estimated via the evidence lower bound (ELBO), and employs a Semi-deterministic Monte Carlo (SDMC) scheme to mitigate the variance explosion inherent in double Monte Carlo estimators. The approach is theoretically justified and empirically validated, demonstrating consistent improvements over pretrained checkpoints and outperforming state-of-the-art baselines across math, reasoning, and coding tasks.

Diffusion LLMs and RL Fine-Tuning

DLMs operate by progressively corrupting sequences with masking noise and training models to reconstruct the original data. The forward process masks tokens independently with probability $t$, while the reverse process iteratively denoises masked sequences. The training objective is a denoising loss, which provides a lower bound on the sequence likelihood (ELBO). Unlike autoregressive models, DLMs lack a natural token-level factorization, complicating the application of RL methods that rely on token-level likelihoods and importance ratios.

GRPO, a value-network-free RL algorithm, estimates advantages from group statistics of sampled completions. In DLMs, the absence of tractable token-level likelihoods necessitates sequence-level objectives. Previous adaptations, such as diffu-GRPO, used mean-field approximations for token likelihoods, but these methods discard token correlations and introduce bias.

Variance Decomposition and ELBO Estimation

A central contribution of the paper is the analysis of variance sources in ELBO estimation. The ELBO involves two stochastic components: sampling the noise level $t$ (masking ratio) and sampling the masked sequence $y_t$. Empirical analysis reveals that variance is dominated by the choice of $t$, while the loss function as a function of $t$ exhibits a smooth, convex structure across prompts.

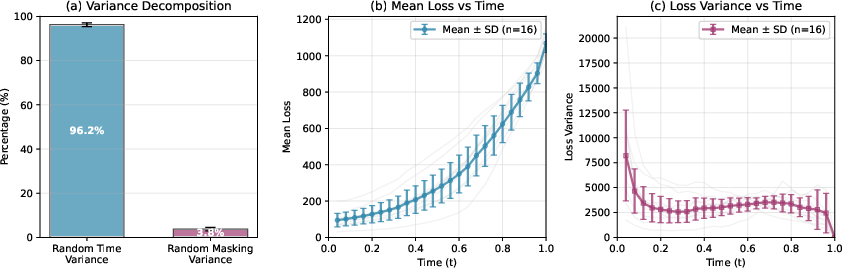
Figure 1: The mean and variance of the loss function as a function of noise level $t$; variance is dominated by random time sampling, and the loss curve is smooth and predictable.

This motivates the use of deterministic integration over $t$ (numerical quadrature) and limited Monte Carlo sampling for $y_t$, forming the SDMC estimator. Theoretical analysis shows that, under mild regularity conditions, the SDMC estimator achieves lower bias and variance than double Monte Carlo, with most gains realized using only 2–3 quadrature points.

Group Diffusion Policy Optimization (GDPO)

GDPO reformulates the RL objective for DLMs by using sequence-level ELBO estimates for importance weighting and advantage calculation. The algorithm proceeds as follows:

1. For each prompt, sample $G$ completions from the current policy.
2. Estimate sequence-level likelihoods via SDMC quadrature over $N$ fixed time points.
3. Compute sequence-level importance ratios and unnormalized advantages.
4. Update the policy using the GDPO loss, which incorporates clipped importance weights and a KL regularization term.

The SDMC estimator is implemented using Gaussian quadrature, and the number of network evaluations per likelihood computation equals the number of quadrature points. Empirical results confirm that quadrature-based estimators yield lower bias and variance than naive Monte Carlo, with substantial efficiency gains.

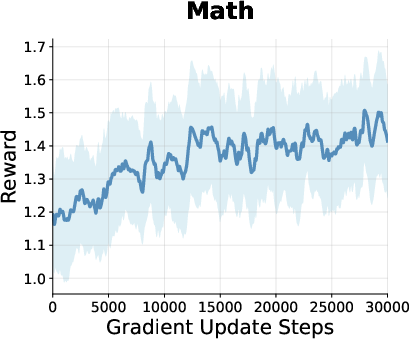
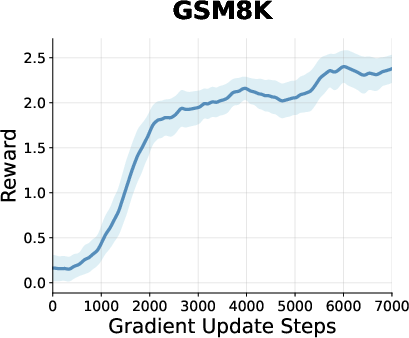
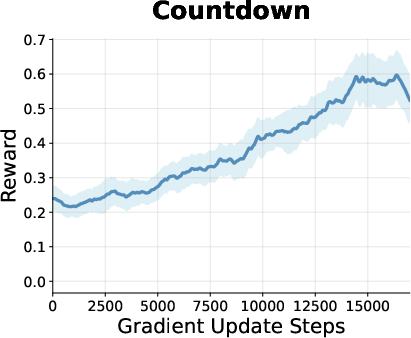
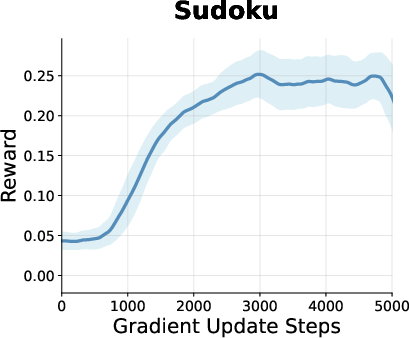
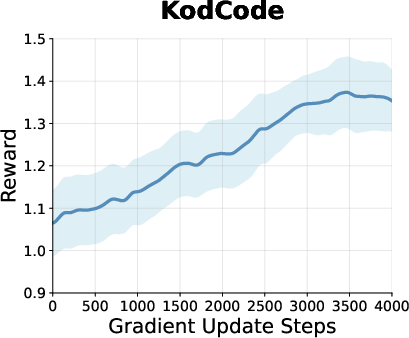
Figure 2: Reward curves during RL training for models on math, planning, and coding tasks, showing steady improvement and plateauing behavior for GDPO.

Empirical Results

GDPO is evaluated on a suite of reasoning, planning, and coding benchmarks, including GSM8K, MATH500, Countdown, Sudoku, HumanEval, and MBPP. The base model is LLaDA-8B-Instruct, an open-source DLM. GDPO consistently improves upon the checkpoint and outperforms diffu-GRPO and SFT+diffu-GRPO baselines, often without requiring supervised fine-tuning.

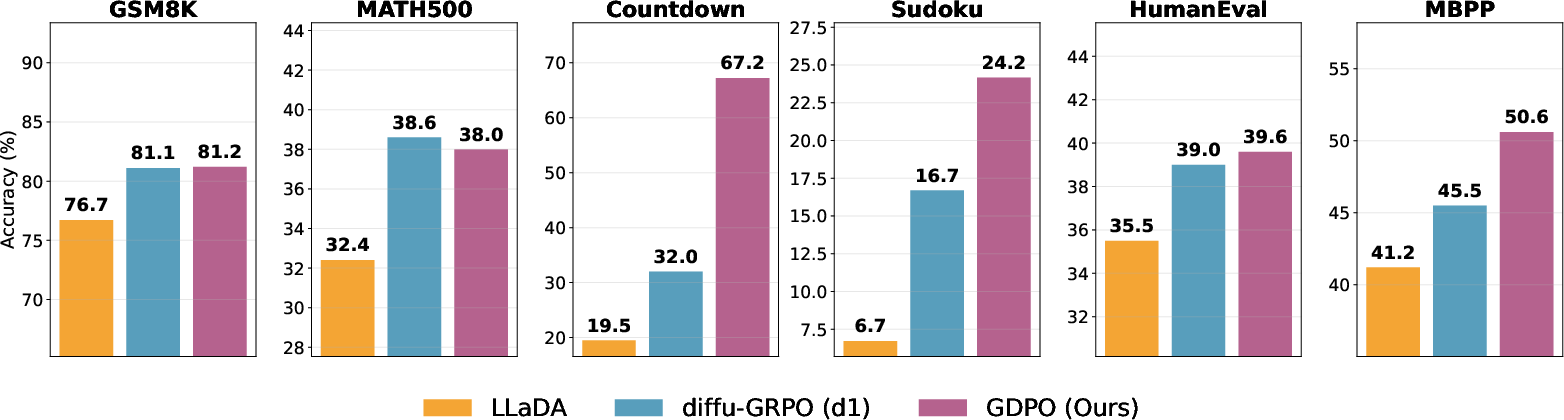
Figure 3: GDPO significantly outperforms the baseline (LLada) and other RL methods (diffu-GRPO) across reasoning, planning, and coding tasks.

Key findings include:

• Superior performance on long sequences: GDPO generalizes better to longer contexts, attributed to sequence-level likelihoods promoting uniform improvements across token positions.
• Computational efficiency: GDPO achieves strong results with modest hardware (2–4 H100 GPUs for most tasks), making it accessible for practitioners with limited resources.
• Estimator accuracy matters: More accurate ELBO approximations directly translate to improved RL fine-tuning outcomes, as demonstrated on the Countdown dataset.

Theoretical Analysis

The paper provides rigorous error bounds for the SDMC estimator. Under general conditions, the mean squared error (MSE) decomposes into Monte Carlo variance ($O(1/NK)$) and integration bias ($O(1/N^2)$ for Riemann sums, $O(1/N^4)$ or $O(1/N^8)$ for quadrature). With additional smoothness assumptions, the variance term can scale as $O(1/N^2K)$. The integrand is shown to be a Bernstein polynomial, monotone and convex under reasonable conditions, justifying the use of quadrature.

Implementation Considerations

• Quadrature points: Empirical and theoretical analysis suggest that 2–3 quadrature points suffice for accurate ELBO estimation.
• Batch size and hardware: The method is compatible with standard RL libraries (e.g., TRL), and training can be performed efficiently on commodity hardware.
• Learning rate sensitivity: GDPO requires a smaller learning rate than diffu-GRPO to avoid divergence.
• Reward design: Task-specific reward functions are critical for effective RL fine-tuning.

Implications and Future Directions

GDPO establishes a principled and efficient paradigm for RL-based alignment of DLMs, overcoming the variance–cost dilemma of sequence-level likelihood estimation. The use of SDMC sampling is broadly applicable to other generative models with intractable likelihoods. Future work may explore adaptive, data-driven quadrature schemes and further integration of supervised and RL objectives. The demonstrated improvements in reasoning, planning, and coding tasks suggest that DLMs, when properly aligned, can match or exceed autoregressive LLMs in complex domains.

Conclusion

Group Diffusion Policy Optimization (GDPO) advances RL fine-tuning for diffusion LLMs by leveraging sequence-level ELBO estimation via Semi-deterministic Monte Carlo sampling. The approach is theoretically sound, computationally efficient, and empirically superior to prior methods. GDPO's design and analysis provide a robust foundation for future research in DLM alignment and open new avenues for efficient, high-quality reasoning in generative LLMs.