Geometric-Mean Policy Optimization (2507.20673v1)

Abstract: Recent advancements, such as Group Relative Policy Optimization (GRPO), have enhanced the reasoning capabilities of LLMs by optimizing the arithmetic mean of token-level rewards. However, GRPO suffers from unstable policy updates when processing tokens with outlier importance-weighted rewards, which manifests as extreme importance sampling ratios during training, i.e., the ratio between the sampling probabilities assigned to a token by the current and old policies. In this work, we propose Geometric-Mean Policy Optimization (GMPO), a stabilized variant of GRPO. Instead of optimizing the arithmetic mean, GMPO maximizes the geometric mean of token-level rewards, which is inherently less sensitive to outliers and maintains a more stable range of importance sampling ratio. In addition, we provide comprehensive theoretical and experimental analysis to justify the design and stability benefits of GMPO. Beyond improved stability, GMPO-7B outperforms GRPO by an average of 4.1% on multiple mathematical benchmarks and 1.4% on multimodal reasoning benchmark, including AIME24, AMC, MATH500, OlympiadBench, Minerva, and Geometry3K. Code is available at https://github.com/callsys/GMPO.

• The paper introduces GMPO, which uses a geometric-mean objective to reduce sensitivity to outlier token rewards in LLM training.
• It integrates token-level clipping and log-space aggregation, leading to more stable policy updates and improved exploration.
• Empirical tests show GMPO achieves a 4.1% boost in Pass@1 accuracy on reasoning benchmarks and better performance on multimodal tasks.

Geometric-Mean Policy Optimization: Stabilizing RL for LLM Reasoning

Introduction

The paper "Geometric-Mean Policy Optimization" (GMPO) (2507.20673) addresses a critical challenge in reinforcement learning (RL) for LLMs: the instability of policy updates when optimizing token-level rewards, particularly in the context of complex reasoning tasks. Building on the Group Relative Policy Optimization (GRPO) framework, the authors propose a geometric mean-based objective that is less sensitive to outliers in importance-weighted rewards, resulting in more stable and effective policy optimization. The work is supported by both theoretical analysis and extensive empirical evaluation on mathematical and multimodal reasoning benchmarks.

Figure 1: Comparison between GRPO (arithmetic mean) and GMPO (geometric mean) objectives, and the resulting importance sampling ratio distributions during training.

Background and Motivation

GRPO has emerged as a strong PPO variant for LLM post-training, leveraging group-based relative rewards to avoid the need for value models and to improve training efficiency. However, GRPO's reliance on the arithmetic mean of token-level importance-weighted rewards makes it susceptible to instability: outlier tokens with extreme importance sampling ratios can dominate updates, leading to aggressive and unreliable policy changes. While clipping the importance sampling ratio can mitigate this, it also restricts policy exploration and can cause premature convergence to deterministic policies.

The instability is empirically evident: as training progresses, the range of importance sampling ratios in GRPO expands, indicating increasingly aggressive updates and degraded performance. The need for a more robust aggregation method for token-level rewards is clear.

Geometric-Mean Policy Optimization: Methodology

GMPO replaces the arithmetic mean in the GRPO objective with a geometric mean over token-level importance-weighted rewards. Formally, for a rollout $o_i$ of length $|o_i|$, the GMPO objective is:

$$\mathcal{J}_{\mathrm{GMPO}}(\pi_\theta) = \mathbb{E}_{q, \{o_i\}} \left[ \frac{1}{G} \sum_{i=1}^G \left( \prod_{t=1}^{|o_i|} \frac{\pi_\theta(o_{i,t}|q,o_{i,<t})}{\pi_{\theta_{\mathrm{old}}}(o_{i,t}|q,o_{i,<t})} |\hat{A}_i| \right)^{\frac{1}{|o_i|} \mathrm{sgn}(\hat{A}_i)} \right]$$

where $\hat{A}_i$ is the normalized group advantage. The geometric mean is inherently less sensitive to outliers, resulting in a narrower value range for the objective and, consequently, lower variance in policy updates.

The implementation leverages log-space computation for numerical stability, and applies token-level clipping to the importance sampling ratios, as opposed to sequence-level clipping. The token-level approach preserves informative gradient signals and further stabilizes training.

def gmpo_loss(new_probs, old_probs, mask, advantage, epsilon=0.4): new_log_probs, old_log_probs = torch.log(new_probs), torch.log(old_probs) sgn_A = 1 if advantage > 0 else -1 sgn_A_log_probs_diff = sgn_A * (new_log_probs - old_log_probs) sgn_A_log_probs_diff2 = torch.clamp(sgn_A_log_probs_diff, -epsilon, epsilon) sgn_A_log_probs_diff_min = torch.min(sgn_A_log_probs_diff, sgn_A_log_probs_diff2) log_probs_diff_min = sgn_A * sgn_A_log_probs_diff_min importance_sampling_ratio = torch.exp(log_probs_diff_min[mask].sum()/mask.sum()) loss = -advantage * importance_sampling_ratio return loss

Theoretical and Empirical Analysis

The authors provide a rigorous analysis of the stability benefits of GMPO. The geometric mean objective is shown to have a provably narrower value range than the arithmetic mean, directly reducing the variance of policy updates. From a gradient perspective, GMPO aggregates token gradients using the geometric mean of importance sampling ratios, which is robust to extreme values, whereas GRPO's arithmetic mean can be dominated by outliers.

Empirical results confirm these theoretical advantages. GMPO maintains a much more stable range of importance sampling ratios throughout training, even when the clipping range is widened to encourage exploration.

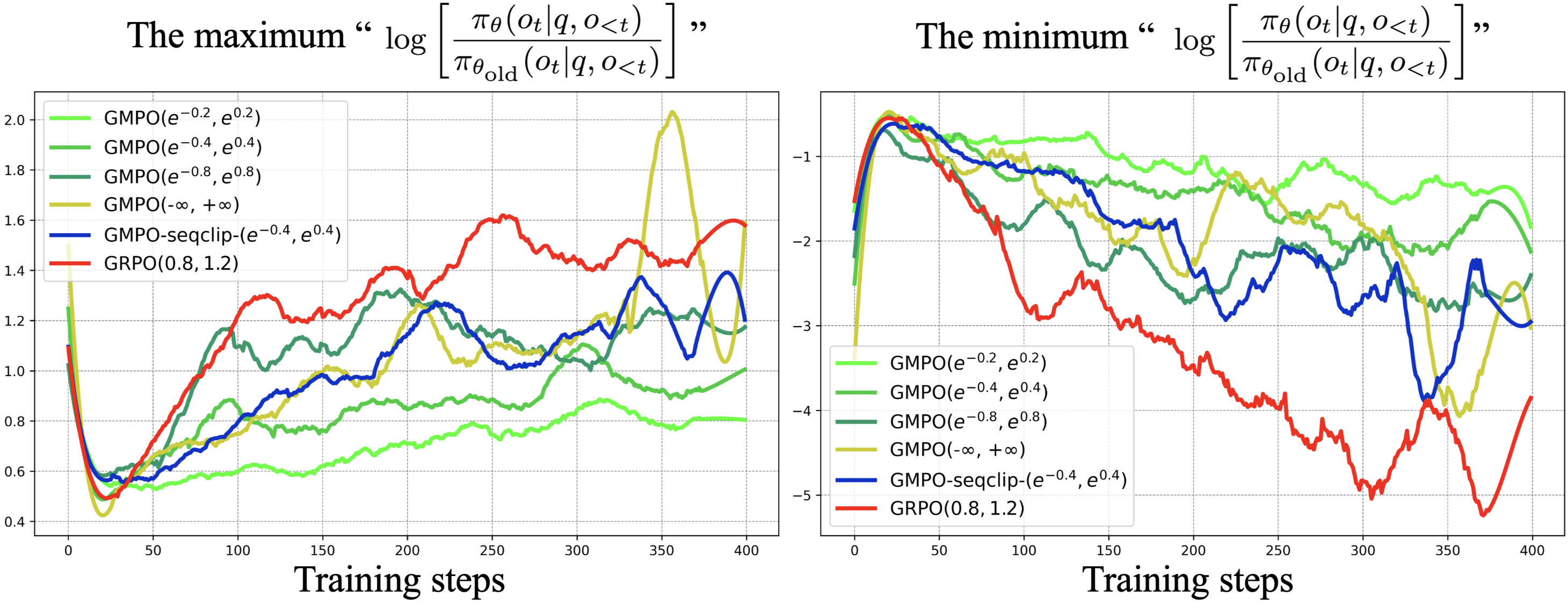
Figure 2: GMPO maintains a narrower and more stable range of importance sampling ratios compared to GRPO, even with a larger clip range.

Further, GMPO consistently maintains higher token entropy and lower KL divergence from the pre-RL model, indicating both improved exploration and reduced risk of overfitting. On challenging datasets, GMPO achieves higher and more stable training rewards than GRPO.

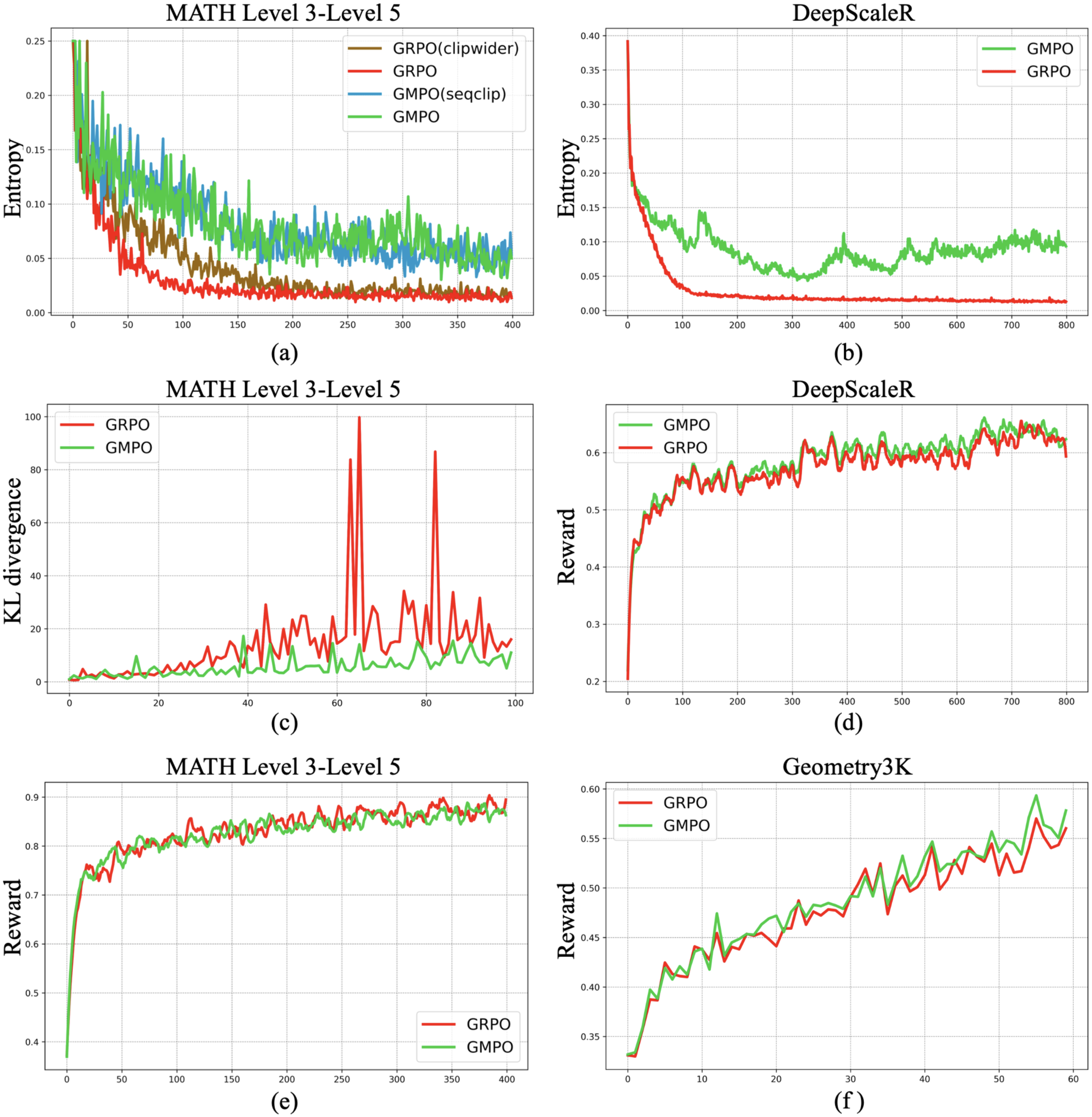
Figure 3: GMPO exhibits higher entropy, lower KL divergence, and superior training rewards compared to GRPO across multiple datasets.

Experimental Results

GMPO is evaluated on a suite of mathematical reasoning benchmarks (AIME24, AMC, MATH500, Minerva, OlympiadBench) and the multimodal Geometry3K dataset. Across all settings, GMPO outperforms GRPO and other strong baselines:

• On five mathematical reasoning benchmarks, GMPO-7B achieves an average Pass@1 accuracy of 63.4%, a 4.1% improvement over GRPO.
• On the Geometry3K multimodal benchmark, GMPO improves Pass@1 accuracy by 1.4% over GRPO.

Ablation studies demonstrate that the geometric mean objective, token-level clipping, and appropriate normalization are all critical for optimal performance and stability. Notably, removing the normalization term or using sequence-level clipping degrades performance and increases instability.

Practical Implications and Future Directions

GMPO provides a robust and scalable RL framework for LLM post-training, particularly in domains requiring complex reasoning and long-horizon credit assignment. The geometric mean objective enables stable policy optimization without sacrificing exploration, and the token-level clipping strategy further enhances reliability.

Practically, GMPO can be integrated into existing RL pipelines for LLMs with minimal modification, as the core change is in the aggregation of token-level rewards and the application of log-space geometric mean computation. The method is compatible with large-scale distributed training and can be applied to both language-only and multimodal models.

Theoretically, the work suggests that robust aggregation methods—beyond the arithmetic mean—are essential for stable RL in high-variance, high-dimensional settings such as LLMs. Future research may explore further generalizations, such as other robust means or adaptive aggregation strategies, and extend the approach to other RL domains with similar instability issues.

Conclusion

Geometric-Mean Policy Optimization (GMPO) advances the state of RL for LLMs by addressing the instability inherent in arithmetic mean-based objectives. By optimizing the geometric mean of token-level rewards and employing token-level clipping, GMPO achieves more stable, reliable, and effective policy updates. The method demonstrates superior performance on both language and multimodal reasoning tasks, and its design principles are broadly applicable to RL in high-variance environments. This work provides a foundation for future research on robust and scalable RL algorithms for complex generative models.