Sample More to Think Less: Group Filtered Policy Optimization for Concise Reasoning (2508.09726v1)

Abstract: LLMs trained with reinforcement learning with verifiable rewards tend to trade accuracy for length--inflating response lengths to achieve gains in accuracy. While longer answers may be warranted for harder problems, many tokens are merely "filler": repetitive, verbose text that makes no real progress. We introduce GFPO (Group Filtered Policy Optimization), which curbs this length explosion by sampling larger groups per problem during training and filtering responses to train on based on two key metrics: (1) response length and (2) token efficiency: reward per token ratio. By sampling more at training time, we teach models to think less at inference time. On the Phi-4-reasoning model, GFPO cuts GRPO's length inflation by 46-71% across challenging STEM and coding benchmarks (AIME 24/25, GPQA, Omni-MATH, LiveCodeBench) while maintaining accuracy. Optimizing for reward per token further increases reductions in length inflation to 71-85%. We also propose Adaptive Difficulty GFPO, which dynamically allocates more training resources to harder problems based on real-time difficulty estimates, improving the balance between computational efficiency and accuracy especially on difficult questions. GFPO demonstrates that increased training-time compute directly translates to reduced test-time compute--a simple yet effective trade-off for efficient reasoning.

• The paper introduces GFPO, a method that selectively trains on the top-k candidate responses to minimize verbose reasoning without sacrificing accuracy.
• It demonstrates that reducing response lengths can yield up to 84.6% token efficiency improvements on benchmarks like AIME and GPQA while preserving performance.
• The methodology leverages group sampling and filtering techniques to shape reward signals in reinforcement learning, offering practical benefits for efficient inference.

Group Filtered Policy Optimization: Efficient Reasoning via Selective Training

Introduction

The paper "Sample More to Think Less: Group Filtered Policy Optimization for Concise Reasoning" (2508.09726) addresses a critical inefficiency in reinforcement learning from verifier rewards (RLVR) for LLMs: the tendency for models trained with methods like GRPO to produce excessively verbose reasoning chains, often with little correlation between length and correctness. The authors introduce Group Filtered Policy Optimization (GFPO), a method that samples larger groups of candidate responses during training and filters them based on response length or token efficiency, thereby curbing length inflation while maintaining accuracy. The approach is evaluated on challenging STEM and coding benchmarks, demonstrating substantial reductions in response length with no statistically significant loss in accuracy.

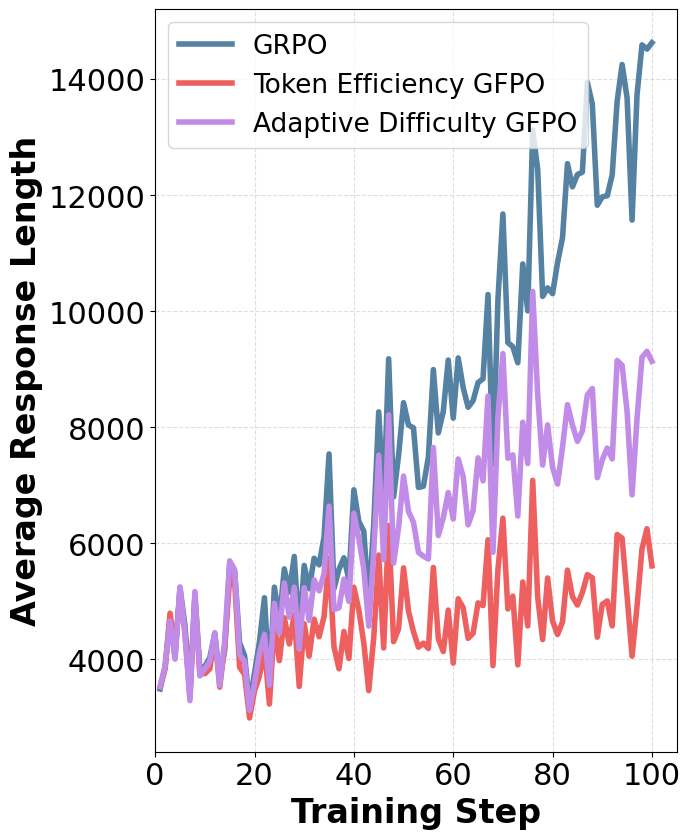
Figure 1: GFPO modifies GRPO by sampling more responses, ranking by a target attribute (e.g., length, token efficiency), and learning only from the top-k, thereby shaping the policy toward concise reasoning and curbing length inflation.

Motivation and Background

RLVR methods such as GRPO and PPO have enabled LLMs to scale their reasoning at inference time, but at the cost of significant response length inflation. Empirical analysis reveals that longer responses are often less accurate, and that length increases are not always justified by problem difficulty. Prior attempts to mitigate this, such as token-level loss normalization (e.g., DAPO, Dr. GRPO), have proven insufficient, as they can inadvertently reinforce verbosity in correct responses. The need for models that retain high reasoning accuracy while producing concise outputs motivates the development of GFPO.

Methodology: Group Filtered Policy Optimization

GFPO extends GRPO by introducing a selective learning mechanism:

• Sampling: For each training instance, a larger group of candidate responses ($G$) is sampled from the current policy.
• Filtering: Responses are ranked according to a user-specified metric (e.g., response length, token efficiency), and only the top-$k$ are retained for policy gradient updates. The rest receive zero advantage.
• Advantage Estimation: Advantages are normalized within the retained subset, ensuring that only the most desirable responses influence learning.

This approach serves as an implicit form of reward shaping, enabling simultaneous optimization for multiple response attributes without complex reward engineering. GFPO is compatible with any GRPO variant and can be paired with different loss normalization strategies.

Experimental Setup

• Model: Phi-4-reasoning (14B parameters), SFT baseline.
• Baselines: GRPO-trained Phi-4-reasoning-plus.
• Datasets: AIME 24/25, GPQA, Omni-MATH, LiveCodeBench.
• Training: 100 RL steps, batch size 64, group sizes $G \in \{8, 16, 24\}$, with $k \leq 8$ for fair comparison.
• Metrics: Pass@1 accuracy, average response length, excess length reduction (ELR).

Results

Length Reduction and Accuracy Preservation

GFPO achieves substantial reductions in response length inflation across all benchmarks, with no statistically significant drop in accuracy compared to GRPO. For example, optimizing for length with Shortest 4/24 GFPO yields 46.1% (AIME 25), 59.8% (AIME 24), and 57.3% (GPQA) reductions in excess length. Token Efficiency GFPO achieves even larger reductions (up to 84.6% on AIME 24), with only minor, non-significant accuracy dips.

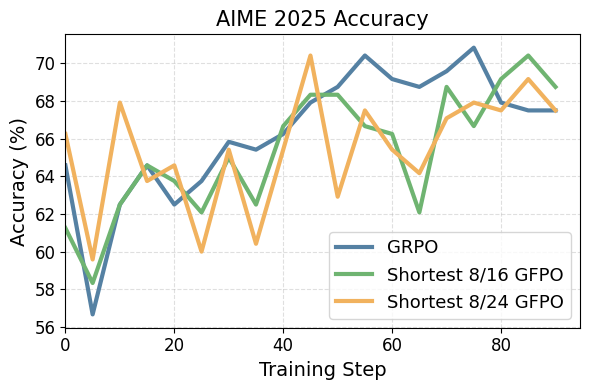
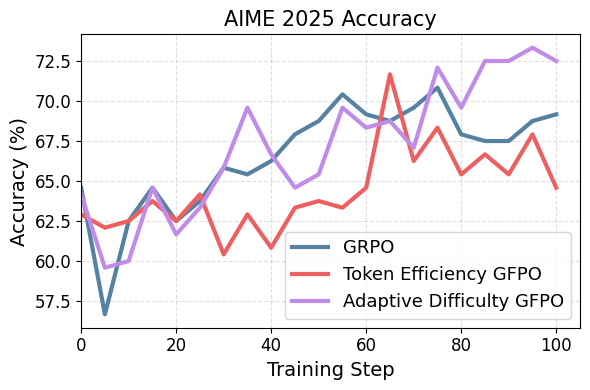
Figure 2: GFPO variants reach the same peak accuracy as GRPO on AIME 25 during training.

Figure 3: Pareto frontier analysis shows that for most benchmarks, at least one GFPO variant strictly dominates GRPO, achieving both higher accuracy and shorter responses.

Effect of Sampling and Filtering

The key lever for controlling response length is the $k/G$ ratio. Lowering $k$ or increasing $G$ enables more aggressive filtering, with diminishing returns beyond a certain point. Token Efficiency GFPO, which ranks by reward per token, provides the strongest length reductions, especially on easier problems, while Adaptive Difficulty GFPO dynamically allocates $k$ based on real-time difficulty estimates, yielding the best trade-off on the hardest problems.

Robustness Across Problem Difficulty

GFPO reduces verbosity across all difficulty levels. Token Efficiency GFPO produces responses even shorter than the SFT baseline on easy questions, while Adaptive Difficulty GFPO achieves the highest accuracy on the hardest problems by allocating more training signal to them.

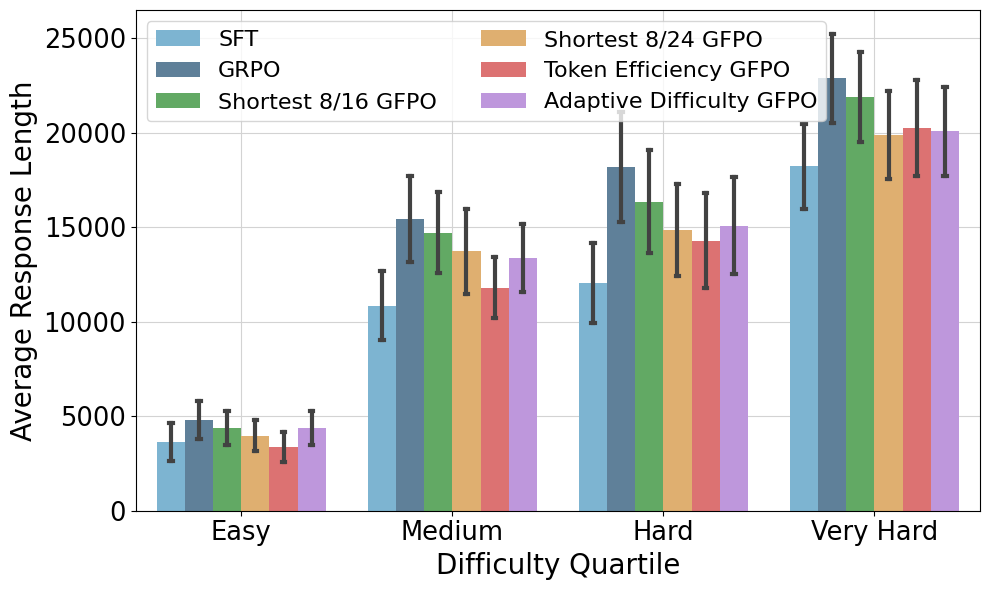
Figure 4: Average response length increases with problem difficulty for all methods, but GFPO consistently reduces length across all levels.

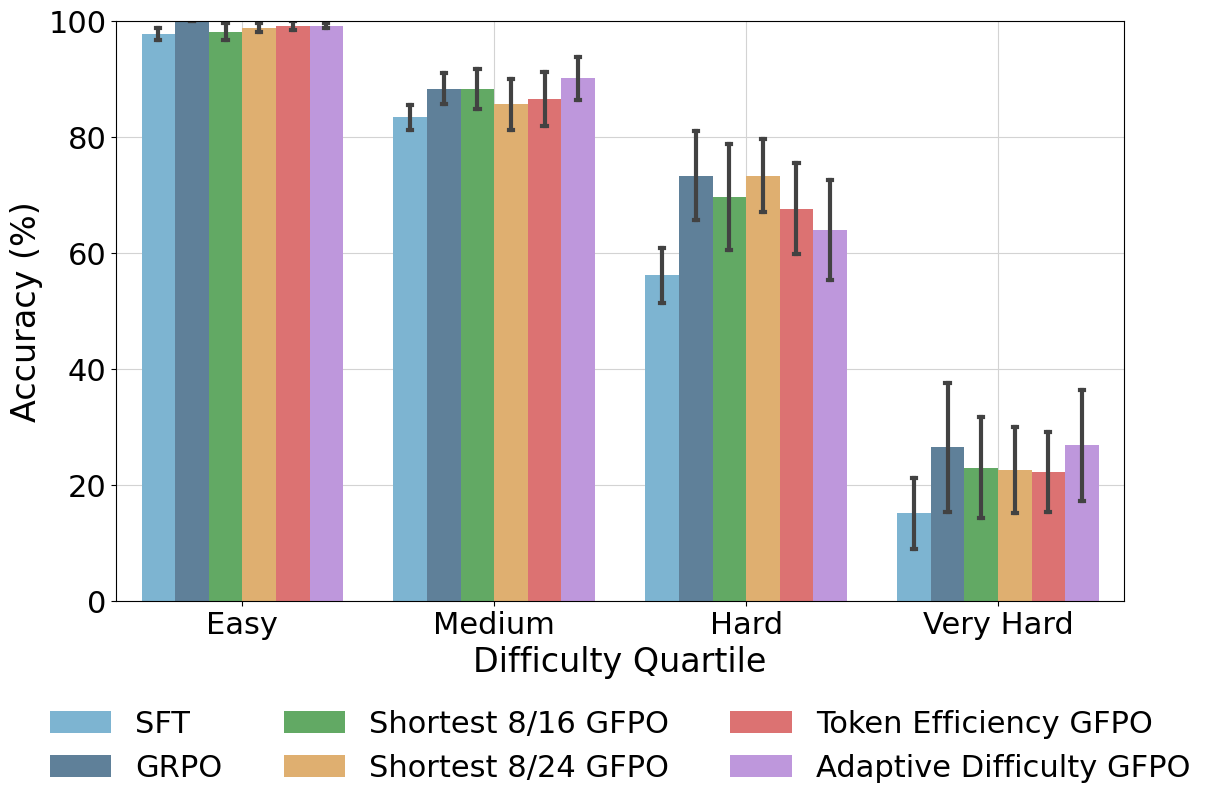
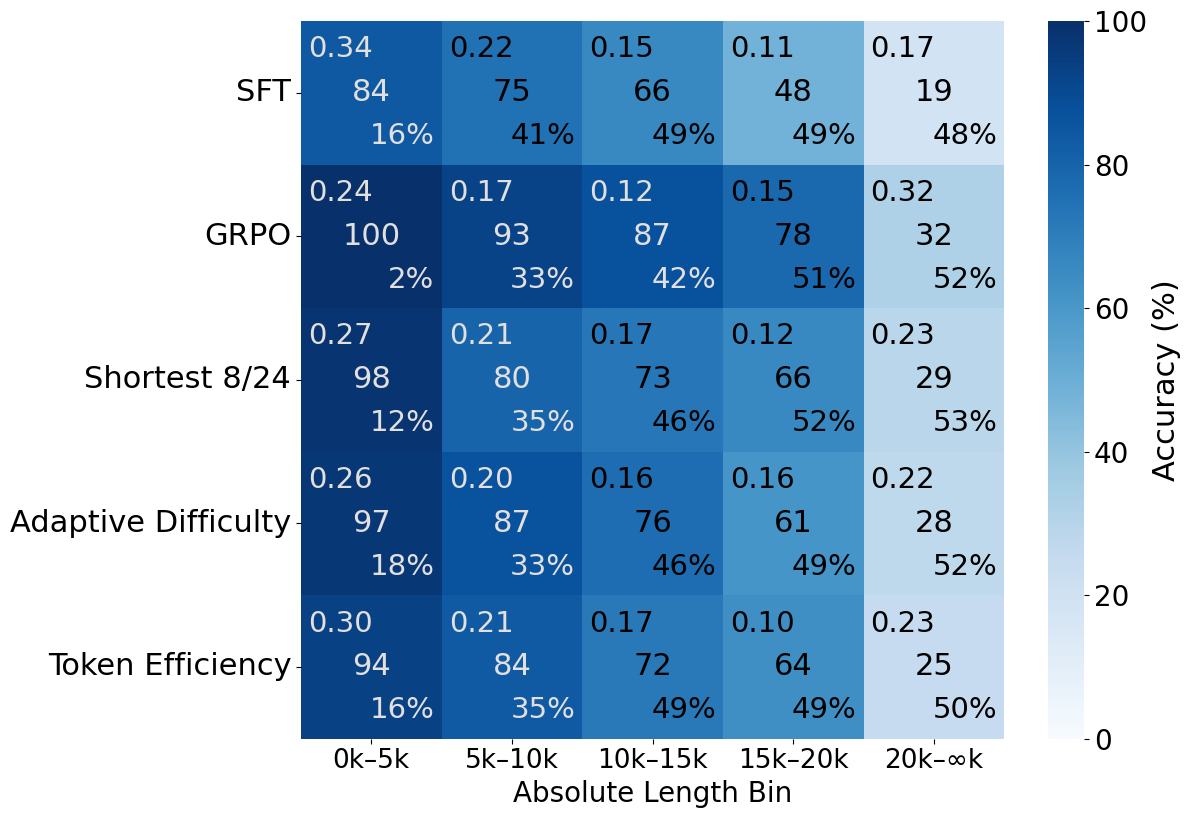
Figure 5: Adaptive Difficulty and Shortest 8/24 GFPO maintain or exceed GRPO accuracy on hard and very hard problems, with Token Efficiency GFPO showing small, non-significant drops.

Qualitative and Structural Analysis

GFPO's length reductions are concentrated in the solution and verification phases of reasoning traces, with minimal impact on the problem statement and final answer. For example, Shortest 8/24 GFPO cuts solution length by 94.4% and verification length by 66.7% on AIME 25.

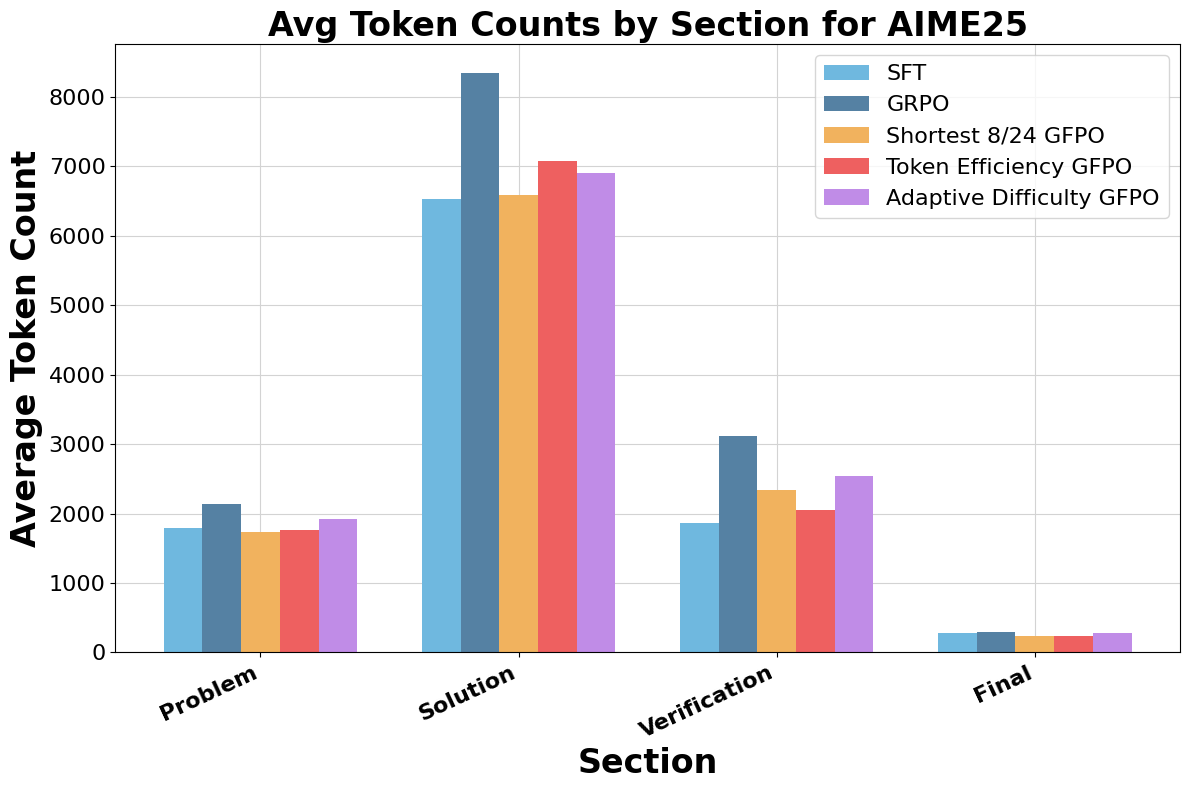
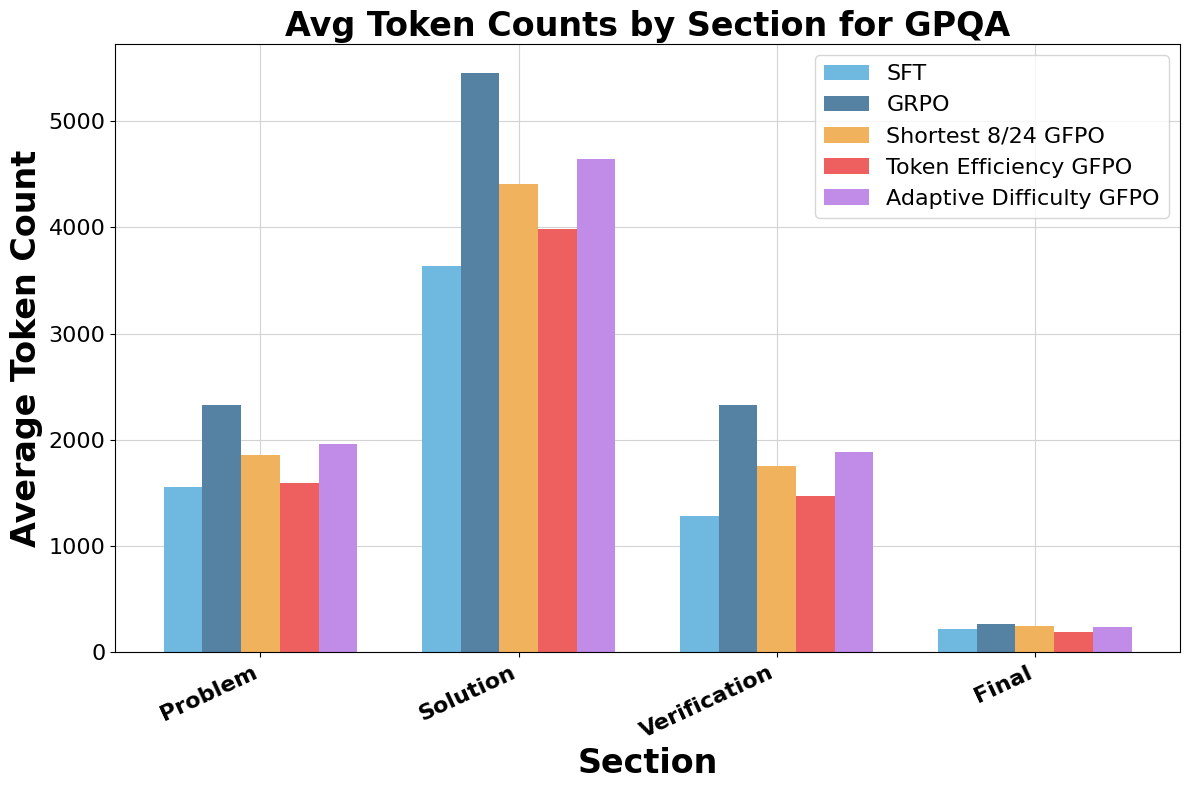
Figure 6: Token analysis shows that GFPO variants markedly reduce verbosity in the solution and verification phases compared to GRPO.

Qualitative comparisons further illustrate that GFPO-trained models avoid redundant recomputation and focus on the most direct solution paths.

Implications and Future Directions

GFPO demonstrates that increased training-time compute (via larger group sampling) can be traded for persistent inference-time efficiency, a highly desirable property for deployment. The method is general and can be extended to optimize for other attributes (e.g., factuality, safety) by changing the filtering metric. The approach is orthogonal to reward engineering and can be combined with more sophisticated reward functions or inference-time interventions for further gains.

The findings challenge the assumption that longer reasoning chains are necessary for harder problems, showing that concise reasoning can be both more efficient and equally accurate. This has implications for the design of future RLHF and RLVR pipelines, especially as LLMs are deployed in resource-constrained or latency-sensitive environments.

Potential future work includes:

• Integrating GFPO with multi-attribute reward models.
• Exploring adaptive group size scheduling based on model uncertainty.
• Combining GFPO with inference-time early stopping or answer convergence signals.
• Applying GFPO to domains beyond STEM and code, such as open-domain dialogue or multi-modal reasoning.

Conclusion

Group Filtered Policy Optimization provides a principled and practical solution to the problem of response length inflation in RLVR-trained LLMs. By sampling more and learning selectively from concise, high-reward responses, GFPO achieves substantial reductions in reasoning chain length while preserving accuracy. The method is simple to implement, generalizable, and offers a favorable trade-off between training and inference compute, making it a valuable addition to the RLHF toolkit for efficient and scalable LLM deployment.