Unlocking the Potential of Difficulty Prior in RL-based Multimodal Reasoning (2505.13261v1)

Abstract: In this work, we investigate how explicitly modeling problem's difficulty prior information shapes the effectiveness of reinforcement learning based fine-tuning for multimodal reasoning. Our exploration mainly comprises of following three perspective: First, through offline data curation, we analyze the U-shaped difficulty distribution of two given datasets using the base model by multi-round sampling, and then filter out prompts that are either too simple or extremely difficult to provide meaningful gradients and perform subsequent two-stage training. Second, we implement an online advantage differentiation, computing group-wise empirical accuracy as a difficulty proxy to adaptively reweight advantages estimation, providing stronger learning signals for more challenging problems. Finally, we introduce difficulty hints as explicit prompts for more complex samples in the second training stage, encouraging the model to calibrate its reasoning depth and perform reflective validation checks. Our comprehensive approach demonstrates significant performances across various multi-modal mathematical reasoning benchmarks with only 2K+0.6K two-stage training data.

• The paper introduces a difficulty prior in RL fine-tuning to improve model performance and overcome flat reward schedules.
• It employs Group Relative Policy Optimization (GRPO) and curated moderate-difficulty samples to stabilize training gradients.
• Experiments on benchmarks like Geometry3K show enhanced data efficiency and improved multimodal reasoning accuracy.

Unlocking the Potential of Difficulty Prior in RL-based Multimodal Reasoning

Introduction

The paper investigates the incorporation of difficulty prior into the reinforcement learning (RL) fine-tuning process for enhancing multimodal reasoning capabilities. The paper addresses three significant limitations in current RL-based finetuning methodologies: mixed-difficulty corpora, flat reward schedules, and an absence of difficulty awareness. By tackling these issues, the paper aims to improve model performance across various multimodal reasoning benchmarks.

Methodology

Reinforcement Learning Fine-Tuning

The paper employs Group Relative Policy Optimization (GRPO) for RL fine-tuning. In GRPO, a LLM is optimized based on a scalar reward signal, utilizing a group-based advantage estimation approach. This method eliminates the need for a value network, enhancing training stability and efficiency.

Offline Data Curation

The offline data curation process involves selecting prompts of moderate difficulty, removing those that are too easy or too hard. This strategy ensures that training focuses on samples that provide meaningful gradients, thereby stabilizing GRPO gradients and avoiding computational waste.

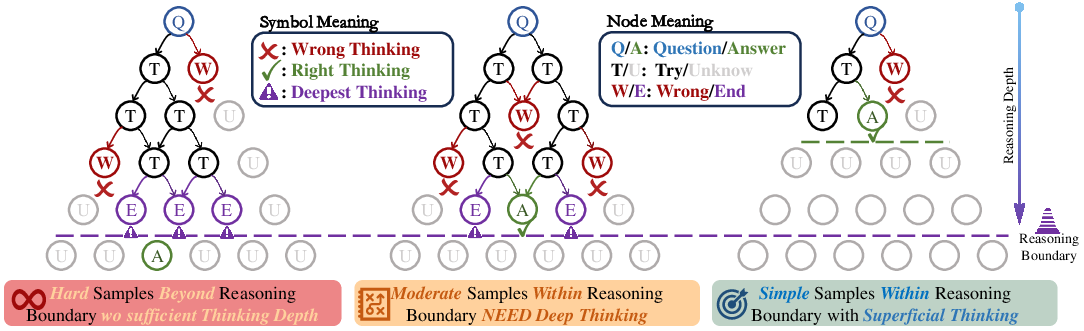
Figure 1: Demonstration of the samples with three difficulty levels, and relation with reasoning boundary and thinking depth: Hard samples lie beyond the reasoning boundary and cannot be answered correctly even after multiple attempts. Moderate samples reside within the reasoning boundary and require deep thinking to arrive at the correct answer. Simple samples stay within the reasoning boundary and can be answered correctly with only shallow or superficial thinking.

Online Advantage Differentiation

During RL fine-tuning, the method calculates a group-wise empirical accuracy to serve as a difficulty proxy, allowing the model to re-weight advantages adaptively. This ensures that correct answers to challenging problems receive stronger gradients, enhancing learning signals for meaningful training.

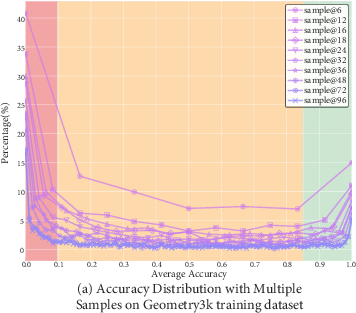
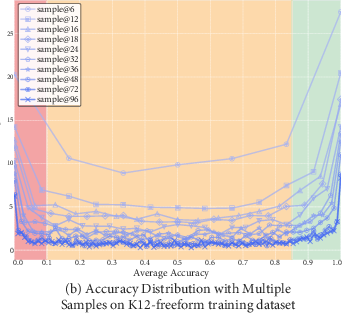
Figure 2: U-Shaped Accuracy Distribution of Model Predictions Across Diverse Sampling Sizes: A comprehensive visual representation of the accuracy distribution across multiple samples from the base model on the Geometry3K and K12-freeform-2.1K datasets.

Implementation

The methodology was tested using datasets like Geometry3K and K12-freeform-2.1K. Multiple sampling rounds estimated accuracy distribution, identifying a U-shaped pattern in difficulty, which guided the data curation process. The advantage differentiation employed several re-weighting functions, including exponential-decay and inverse-proportional functions, to align reward scaling with problem difficulty effectively.

Experiments

The paper conducts comprehensive experiments across multimodal mathematical reasoning benchmarks, showing superior performance compared to other RL, SFT-, or SFT+RL-based models. The data efficiency of the proposed method is notable, achieving excellent results with a significantly smaller dataset.

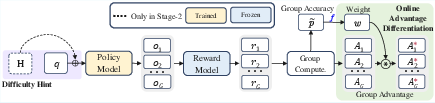
Figure 3: Overall training pipeline for two stages.

Conclusion

The paper demonstrates that modeling difficulty prior in RL-based fine-tuning can significantly enhance multimodal reasoning abilities. By addressing limitations in current methodologies, the proposed approach offers a pathway to more efficient and effective training, suggesting promising future research directions in integrating difficulty awareness into learning models.