Differential Smoothing Mitigates Sharpening and Improves LLM Reasoning (2511.19942v1)

Abstract: It is widely recognized that reinforcement learning (RL) fine-tuning of LLMs often leads to \textit{diversity collapse}, where outputs lack variety. Prior work has proposed a range of heuristics to counteract this effect, but these methods are ad hoc: they frequently trade off correctness for diversity, their effectiveness varies across tasks, and in some cases they even contradict one another. In this work, we place these observations on a rigorous foundation. We first provide a formal proof of why RL fine-tuning exhibits diversity collapse via a selection and reinforcement bias. Next, we make a key observation that any reward modification to address diversity collapse only needs to be applied on the correct trajectories. Building directly on this analysis, we introduce a principled method -- \textit{differential smoothing} -- that provably improves both correctness and diversity, outperforming vanilla RL as well as widely used entropy-based heuristics. Our theory precisely characterizes when existing heuristics help and why they fail, while showing that differential smoothing is universally superior. Extensive experiments with models from 1B to 7B parameters, across domains including CountDown and real-world mathematical reasoning, demonstrate consistent gains. Differential smoothing improves both Pass@1 and Pass@k, with up to 6.7\% improvements on AIME24 dataset.

• The paper demonstrates that Differential Smoothing reshapes reward structures to mitigate diversity collapse during RL fine-tuning of LLMs.
• Extensive experiments reveal up to a 6.7% improvement in mathematical reasoning and a 4% pass@K gain on the Countdown task.
• The approach balances selection and reinforcement biases, providing scalable solutions and solid theoretical insights for RL enhancements.

Differential Smoothing Mitigates Sharpening and Improves LLM Reasoning

Introduction to Diversity Collapse in RL for LLMs

Reinforcement Learning (RL) fine-tuning of LLMs is known to cause diversity collapse, where the output generation diversity significantly diminishes. This process impacts metrics such as Pass@$K$, where RL-tuned models often underperform for large $K$ compared to the original base model. The challenge lies in balancing diversity and accuracy, as existing methods that increase diversity typically degrade accuracy.

To address these issues, this paper introduces a novel method called Differential Smoothing, which provides a theoretically grounded approach to improve both correctness and diversity. The analysis identifies biases introduced by RL: selection bias, where correct trajectories with high base probabilities are preferentially reinforced, and reinforcement bias, where these trajectories receive disproportionately larger updates.

Methodological Foundations of Differential Smoothing

Differential Smoothing proposes reshaping the reward structure to target specific biases. By modifying rewards for correct trajectories to include an entropy penalty, the method counteracts diversity collapse and enhances trajectory sampling diversity. Incorrect trajectories are treated differently by reinforcing correctness, providing a nuanced approach that balances the inherent trade-offs.

For a model, trajectories are delineated based on their correctness, with the reward function adjusted accordingly. This differential approach ensures both principles—selection and reinforcement—are aligned in preventing diversity collapse while maintaining successful trajectories.

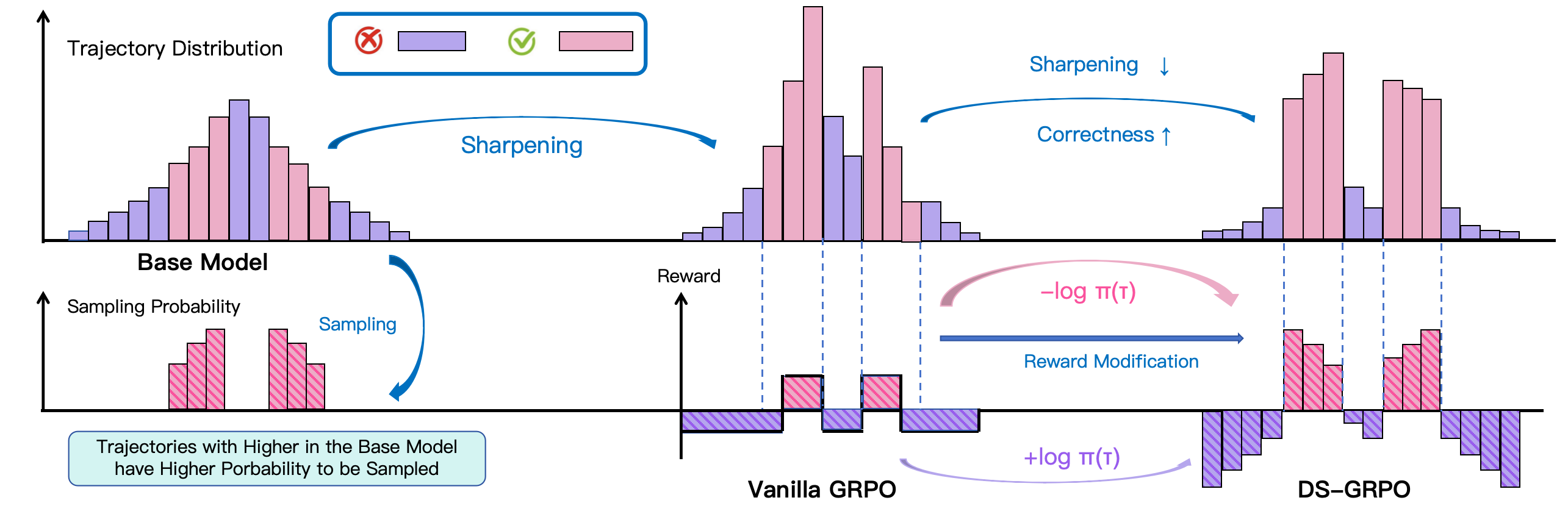
Figure 1: An illustration of the sharpening effect in vanilla RL and the mitigation mechanism of DS-GRPO.

Empirical Validation Across Diverse Tasks

Extensive experiments validate Differential Smoothing's efficacy across various LLMs and tasks. In tests ranging from the Countdown task to complex mathematical reasoning benchmarks, Differential Smoothing consistently improves both Pass@1 and Pass@K metrics.

On the Countdown task, DS-GRPO enhances Pass@K rates by about 4%, accompanied by a notable speedup in inference. For mathematical reasoning benchmarks, Pass@1 and Pass@64 gains are substantial, with up to 6.7% improvement recorded. These results underscore the method's robustness and adaptability across different domains and model architectures.

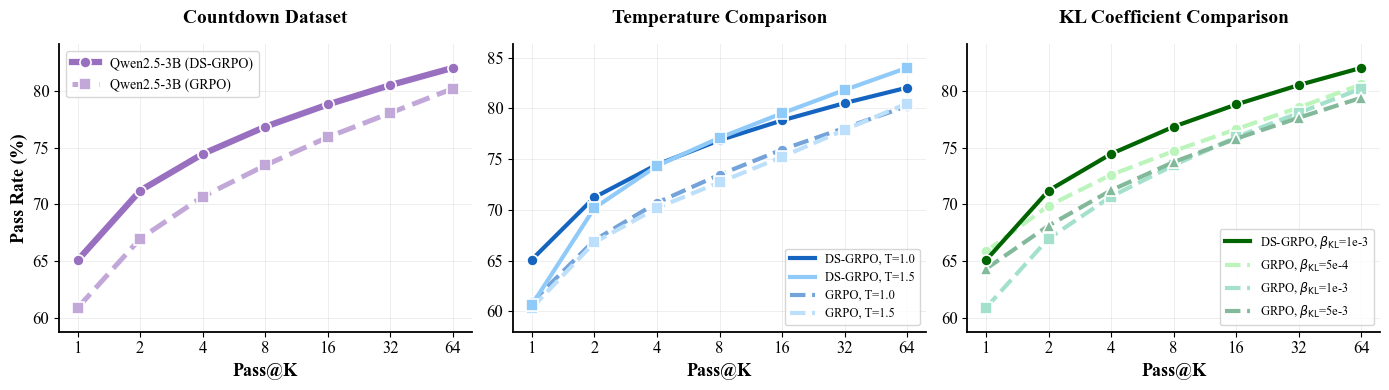
Figure 2: Pass@K performance of DS-GRPO on the Countdown task, compared with GRPO under varying decoding temperatures and KL coefficients.

Implications and Future Developments

The implications of Differential Smoothing span both practical applications and theoretical insights. Practically, it offers a scalable solution to improve LLM performance across tasks where diversity and accuracy are critical. Theoretically, it provides clarity on how entropy manipulation affects distribution shaping in RL.

Future research may explore task-specific tuning of differential rewards, potentially refining the approach to optimize performance further. The nuanced understanding of entropy's role in RL can illuminate broader applications across AI, guiding new methods that consider both exploration and exploitation in model fine-tuning.

Conclusion

Differential Smoothing introduces a principled and empirically validated method to mitigate the diversity collapse common in RL fine-tuning of LLMs. By leveraging targeted reward modifications, it achieves superior performance in correctness and diversity across a range of challenging tasks. This approach sets a foundation for more adaptable and efficient RL-driven model improvements in complex environments.

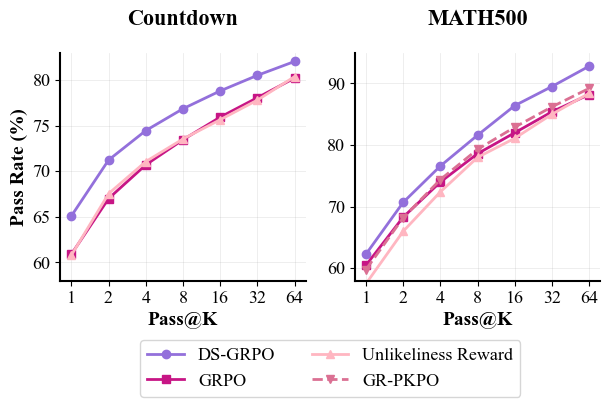
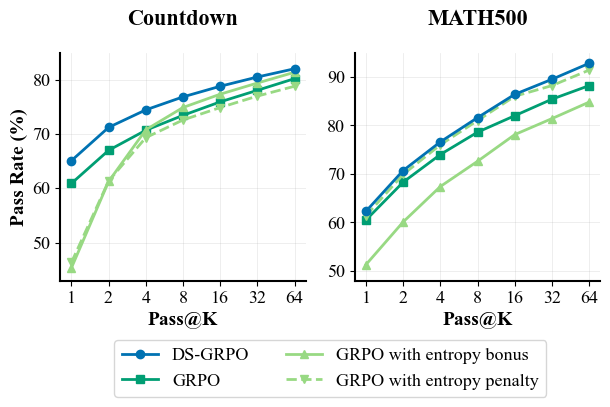
Figure 3: Performance comparisons on MATH500 and Countdown. Left: Comparison among DS-GRPO, GRPO, GR-PKPO.