Risk-Sensitive RL for Alleviating Exploration Dilemmas in Large Language Models (2509.24261v1)

Abstract: Reinforcement Learning with Verifiable Rewards (RLVR) has proven effective for enhancing LLMs on complex reasoning tasks. However, existing methods suffer from an exploration dilemma: the sharply peaked initial policies of pre-trained LLMs confine standard RL algorithms to a narrow set of solutions, boosting single-solution accuracy (pass@1) but suppressing solution diversity and multi-solution performance (pass@k). As a result, RLVR often distills existing capabilities rather than discovering new reasoning strategies. To overcome this, we introduce a Risk-Sensitive Reinforcement Learning framework. Our approach employs a risk-seeking objective that interpolates between mean and maximum rewards, leading to a novel algorithm, Risk-Sensitive GRPO (RS-GRPO), which drives deeper exploration by amplifying learning from challenging prompts. Remarkably, RS-GRPO is simple to implement, requiring only minor code modifications. On six mathematical reasoning benchmarks and with five different LLMs, RS-GRPO consistently improves pass@k performance while maintaining or enhancing pass@1 accuracy.

• The paper presents a novel risk-sensitive reinforcement learning framework that interpolates between mean and max rewards to boost exploration in LLMs.
• It demonstrates that increasing the risk-sensitivity parameter β enhances solution diversity (pass@k) without compromising pass@1 accuracy.
• Experimental results on mathematical reasoning benchmarks show RS-GRPO effectively escapes local optima and achieves global optimization.

Risk-Sensitive RL for Alleviating Exploration Dilemmas in LLMs

Introduction

This paper addresses a significant challenge within the domain of LLM training using RLVR by proposing a novel framework, Risk-Sensitive Reinforcement Learning (RS-RL). Traditional RL methods often boost single-solution accuracy (pass@1) while suppressing solution diversity, causing stagnation in the multi-solution performance metric (pass@k). To overcome this, the paper introduces RS-GRPO, an algorithm designed to amplify exploration by interpolating between mean and maximum rewards. This risk-seeking RL framework is simple to integrate, requiring minimal code changes and shows consistent performance improvement on mathematical reasoning tasks.

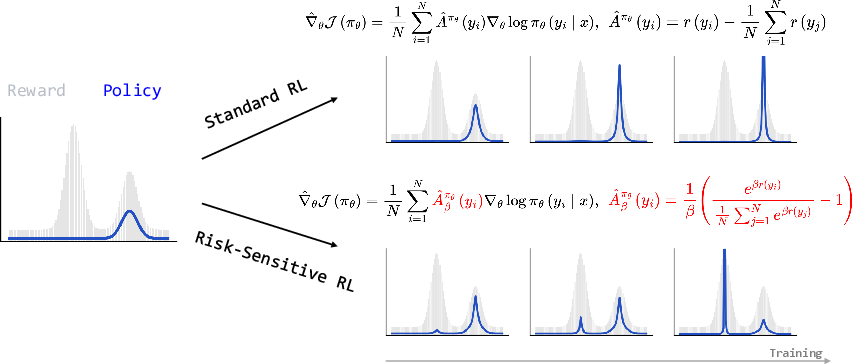
Figure 1: Illustration of the Risk-Sensitive RL vs Standard RL.

The Exploration Dilemma

In reinforcement learning approaches applied to LLMs, a prevalent issue is the sharply peaked initial policies derived from pre-trained models. These peaked distributions limit exploration, as standard RL algorithms often optimize within this narrow parameter space to improve pass@1 accuracy. However, this confines the algorithm’s ability to explore novel reasoning strategies and hampers improvement in pass@k performance.

Risk-Sensitive RL Framework

The RS-RL framework was devised to counteract the exploration dilemma by adopting a risk-seeking approach. The framework utilizes a novel risk-sensitive objective, derived from exponential utility functions, to interpolate smoothly between mean and maximum rewards based on a risk-sensitivity parameter, $\beta$.

For the risk-sensitive policy gradient, the advantage function re-weights prompts by emphasizing scantily explored or challenging areas of the solution space. This approach assists in overcoming local optima that may trap standard RL algorithms and moves the RL process towards global optimization.

Theoretical and Empirical Analysis

To demonstrate the effectiveness of the risk-sensitive approach, the paper provides empirical evidence using bandit experiments that mirror the exploration behavior of RL in LLM settings. The theoretical analysis supports the main claim that increasing $\beta$ enables the policy to favor optimal actions over suboptimal ones in scenarios where standard RL methods falter.

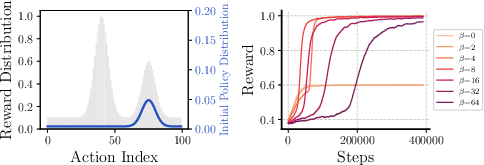
Figure 2: A bandit experiment demonstrating that risk-sensitive RL can escape a local optimum that traps its standard RL counterpart. Standard risk-neutral policies are trapped locally, while risk-sensitive policies converge on the global optimum.

Experiments

In comprehensive experiments spanning multiple LLMs and reasoning benchmarks, RS-GRPO exhibited marked improvement in pass@k performance while maintaining or enhancing pass@1 accuracy, demonstrating a more effective trade-off compared to other existing methods.

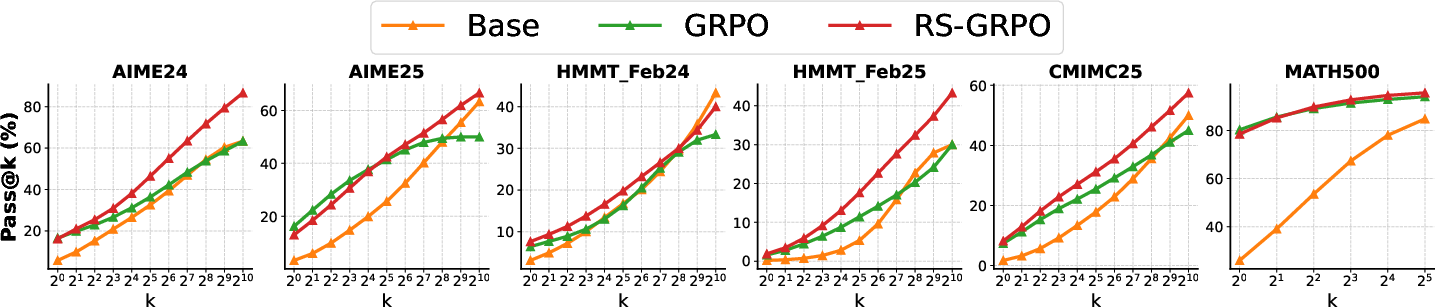
Figure 3: Pass@k performance of RS-GRPO, GRPO, and base models across various benchmarks, illustrating RS-GRPO's superiority in exploring and achieving diverse solutions.

Impact of Risk-Sensitivity Parameter $\beta$

The ablation paper on $\beta$ revealed its critical role in balancing exploration with exploitation. A higher $\beta$ value generally promoted exploration, evidenced by an increased solution diversity and improved pass@k performance without degrading pass@1 accuracy.

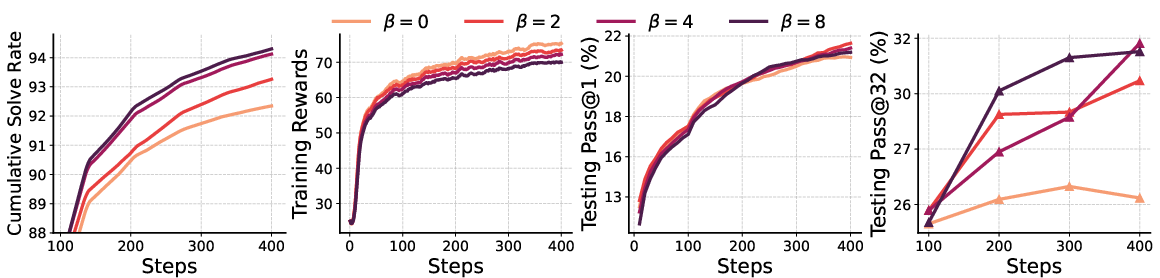
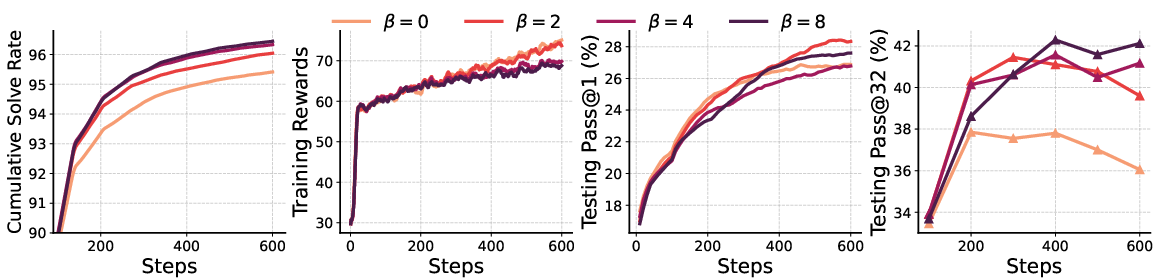
Figure 4: Ablation Study of $\beta$ showcasing its effect on Qwen2.5-Math models during RS-GRPO training.

Conclusion

The introduction of RS-RL provides a substantive leap forward in resolving exploration dilemmas faced by common RL approaches in LLM fine-tuning. By strategically using risk-sensitive objectives, RS-GRPO improves diverse solution discovery in models, preserving high accuracy in reasoning tasks. Future research might explore the applicability of risk-sensitive strategies to various generative modeling domains and their interactions with other exploration techniques.