Information Efficiency of Scientific Automation (2511.15671v1)
Abstract: Scientific discovery can be framed as a thermodynamic process in which an agent invests physical work to acquire information about an environment under a finite work budget. Using established results about the thermodynamics of computing, we derive finite-budget bounds on information gain over rounds of sequential Bayesian learning. We also propose a metric of information-work efficiency, and compare unpartitioned and federated learning strategies under matched work budgets. The presented results offer guidance in the form of bounds and an information efficiency metric for efforts in scientific automation at large.
Sponsored by Paperpile, the PDF & BibTeX manager trusted by top AI labs.
Get 30 days freePaper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper asks: if doing science takes energy (like running experiments, saving data, and resetting instruments), how much new knowledge can we get for a given “energy budget”? The author treats scientific discovery like a physical process, where gathering and storing information costs energy. He builds simple rules and limits that any automated science system must obey, then compares three ways of organizing that system: a single generalist, a single specialist, and a team of specialists that work together (federated learning).
What questions does it try to answer?
- How much information (reduction in uncertainty) can a science system gain if it has only a limited amount of energy to spend?
- What is a fair way to measure “information efficiency,” meaning how much useful knowledge you get per unit of energy?
- Is it better to keep one general system that tries to learn everything, to focus on one narrow area (a specialist), or to split the task into several focused parts that cooperate (federated specialization)?
- When does splitting the problem into parts actually help, and when does it not?
How do they paper the problem?
Think of an automated lab as going through the same 3 steps over and over:
- Measure: run an experiment and record the result.
- Update: adjust your beliefs (your model) using the new result.
- Erase: clear the temporary memory so you can use it again next time.
In everyday terms:
- “Uncertainty” (entropy) is how unsure you are, like how many possible answers are still on the table.
- “Information gain” is how much uncertainty you remove after an experiment—how many wrong possibilities you can cross off.
- “Outcome entropy” is how much raw data you actually keep from each experiment. More data stored means more “stuff” to erase later.
Key physical ideas used:
- Erasing information isn’t free. It costs energy and releases heat (Landauer’s principle). That’s like your phone warming up when deleting a huge cache.
- Measuring and storing results also costs energy, and the cost grows with how much information you extract and how much data you keep.
- Bayesian learning is just a fancy name for updating your best guess as you see new evidence.
The paper defines an “information-work efficiency” score: how many units of information you gain per unit of energy spent. In symbols (you don’t need the details), it’s “information gained divided by energy used,” scaled by a temperature constant. You can think of it as “clues per battery juice.”
They then compare three strategies:
- Generalist: one system tries to learn the whole domain.
- Specialist: one system focuses on a single sub-area.
- Federated specialization: many specialists split the domain and coordinate.
Finally, they run simple computer experiments with a toy formula (a simplified model) to see how these strategies compare across different energy budgets and different degrees of splitting the problem.
What did they find, and why does it matter?
Here are the main findings, framed with simple ideas.
Two fundamental limits
- Prior-limited: If you already know almost everything there is to know about the topic, you can’t extract more than what’s left. No amount of extra energy helps.
- Budget-limited: If you have little energy, your learning is capped by what you can afford to measure and erase.
In both cases, efficiency depends on two levers:
- How much uncertainty you start with in the part of the world you’re trying to learn (effective prior entropy). Less starting uncertainty can make learning “finish” sooner.
- How much data you store from each experiment (outcome entropy). Storing more raw data takes more energy to erase; compressing to the essentials can save energy and improve efficiency.
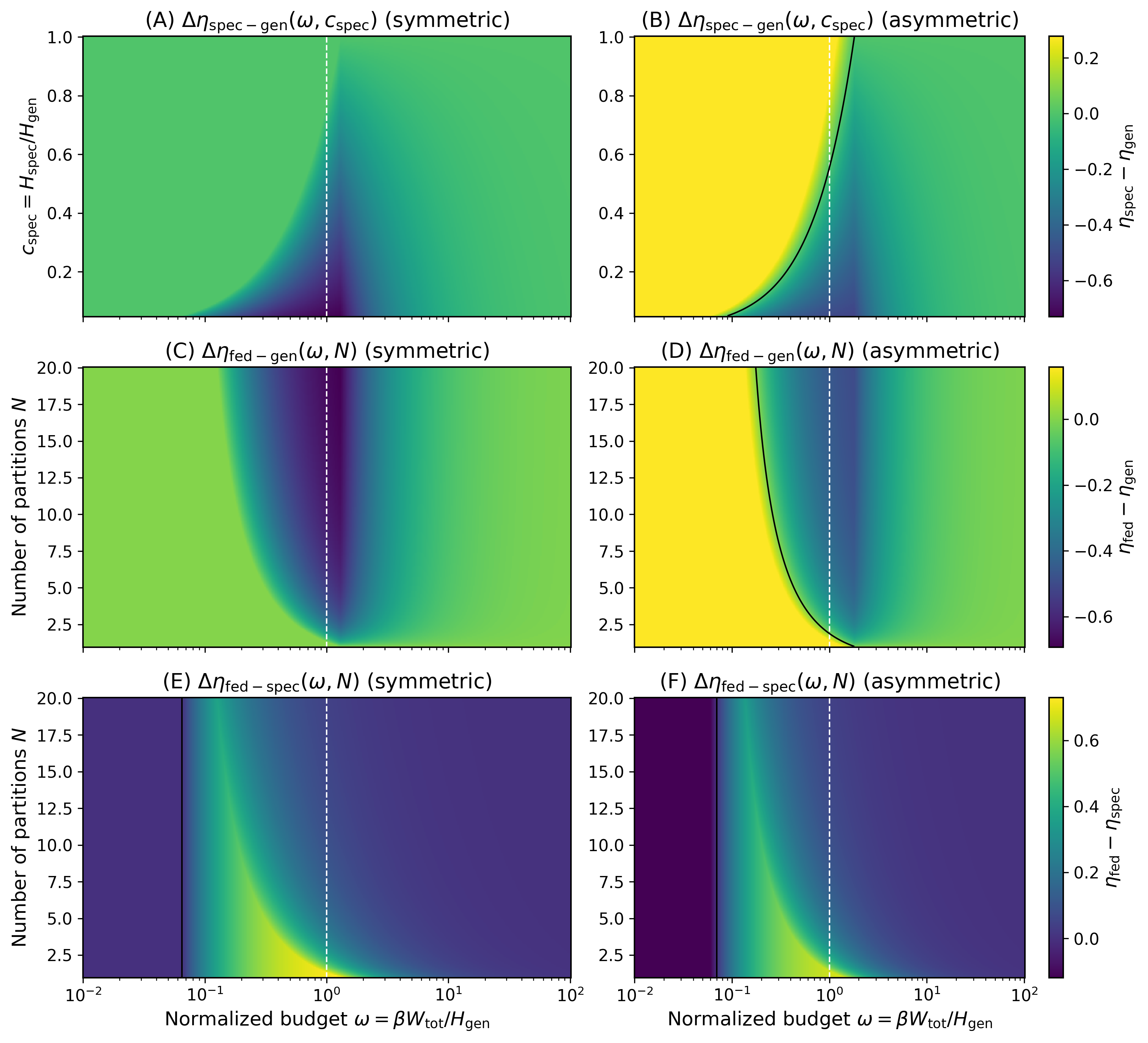
Partitioning (splitting the problem) helps only under certain conditions
- If you split the domain into meaningful subdomains (like chapters in a book), you can reduce the “effective uncertainty” each specialist faces. That’s good.
- But if splitting doesn’t also make measurements simpler or more reversible (lower outcome entropy, less overhead), the generalist can still be more efficient overall.
- In short: splitting helps when it both (a) cuts down the uncertainty each module needs to tackle and (b) makes each measurement-and-erase cycle cheaper.
Comparing strategies
- If all strategies pay the same “overhead” for measuring and erasing (same outcome entropy), the generalist is never beaten in their tests under the same energy budget. Just splitting the problem without reducing measurement overhead doesn’t win.
- If specialists (or federated teams) can be engineered to have lower measurement/erasure overhead (for example, simpler instruments, less noisy data, smarter compression), then:
- At low budgets, specialists and federated teams can be more efficient than a generalist because they waste less energy per experiment.
- With enough partitions and still lower overhead, a federated system can outperform both a generalist and any single specialist over a wide range of budgets. It spreads effort across focused modules, each working efficiently.
What’s the bigger picture?
- For automated science platforms (robotic labs, high-throughput experiments, or AI-driven discovery), energy is a real constraint. You don’t just ask “How fast can we learn?” but also “How efficiently can we turn energy into knowledge?”
- The paper provides a clean way to think about design trade-offs:
- Reduce the starting uncertainty each module faces (smart partitioning).
- Reduce the per-experiment overhead (compress data, design more reversible steps, cut noise).
- It also gives a warning: splitting your system into many specialized parts isn’t automatically better. It helps only when you also lower the “thermodynamic overhead” of measuring and erasing in those parts.
- Practically, this suggests building modular, domain-specific measurement pipelines that produce cleaner, smaller, or better-compressed data, and coordinating them in a federated way. That’s how you can beat a one-size-fits-all generalist under the same energy budget.
Simple takeaways
- Learning costs energy; deleting data costs energy too.
- Efficiency = how much uncertainty you remove per unit of energy.
- You hit two walls: either there’s little left to learn (prior-limited), or you’re short on energy (budget-limited).
- Splitting the problem into parts helps only if it also makes measurements cheaper to store and erase.
- Federated teams of specialists can beat a generalist when they both reduce the uncertainty they face and reduce measurement/erasure overhead.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, concrete list of unresolved issues that future work could address to make the framework operational and empirically grounded.
- Quantify nonzero memory free-energy changes: Replace the idealization ΔF_mem,t≈0 with measured, device-specific ΔF_mem,t and finite-time irreversibility costs; derive tighter bounds for realistic hardware.
- Incorporate actuation/control energy: Extend W_t beyond measurement/erasure to include the physical work of interventions u_t (e.g., robotics, wet-lab operations), and analyze how control energy trades off against information gain.
- Optimal outcome compression: Design and analyze g(Y_t) that minimizes H(S_t) subject to preserving I_t (e.g., minimal sufficient statistics); quantify efficiency gains from compression and the compute/energy required to compress.
- Continuous outcomes and precision: Develop a thermodynamic cost model for analog/continuous measurements, including quantization, resolution selection, and differential entropy pitfalls; map bits-of-precision to energetic costs.
- Joint experiment design for I_t vs H(Y_t): Formulate and solve the control problem of choosing u_t to maximize I_t per unit of outcome entropy and work; characterize Pareto frontiers and optimal policies.
- Computational inference costs: Include the energy/time of Bayesian updates/training (e.g., posterior sampling, gradient-based learning) in W_t; analyze tradeoffs between computational and thermodynamic costs.
- Storage/archival energy accounting: Relax the “negligible archive free energy” assumption by modeling write/read/retention costs of persistent storage; evaluate how storage technology choices shift η.
- Federated coordination overhead: Add communication, synchronization, and consensus energy to federated W_tot; quantify when coordination overhead erodes the partitioning benefits.
- Learning the partition K: Develop algorithms to discover informative partitions (maximize I(Θ;K)) under finite budgets, including the work to classify route-to-subdomain decisions and the cost of misclassification.
- Adaptive/dynamic partitioning: Study how K and p_i should evolve with learning (nonstationary domains); derive policies that adapt partitions online for maximal efficiency.
- Budget allocation across subdomains: Optimize W_toti and the scheduling of rounds to maximize η given (p_i, H_i, α_i); consider bandit-style resource allocation under uncertainty.
- Path-dependence and sequencing: Determine how the order of experiments affects the sum of I_t and H(Y_t); design scheduling heuristics/algorithms that exploit path-dependence to improve efficiency.
- Model misspecification and robustness: Analyze how η and bounds behave when p(y|θ,u) is wrong or misspecified; derive robust or worst-case guarantees (e.g., regret bounds) under model uncertainty.
- Finite-time speed-efficiency tradeoffs: Integrate nonequilibrium thermodynamics to quantify how cycle duration affects minimal work; characterize throughput vs η tradeoffs and optimal cycle times.
- Memory capacity constraints: Examine how limited working registers and finite archive capacity constrain cycles (e.g., selective erasure, caching policies) and impact achievable η.
- Cross-subdomain coupling: Account for mutual information between subdomains (shared structure, transfer learning) rather than treating K-partitions as independent; quantify gains beyond H(Θ|K) compression.
- Fundamental limits linking I_t and H(Y_t): Derive bounds on achievable I_t for a given H(Y_t) (e.g., via channel capacity, Fisher information); use these to guide measurement design under thermodynamic constraints.
- Temperature control costs: Consider non-isothermal operations, cooling/heating energy, and spatial temperature gradients; analyze how controlling T affects budgets and the practicality of approaching bounds.
- Reliability and error-correction overhead: Model energy costs for fault tolerance, redundancy, and error-correcting codes in measurements and memory; quantify their impact on η.
- Formal dominance conditions: Provide a general proof (or counterexamples) for when a generalist strictly dominates federated/specialist strategies under equal outcome entropy, beyond the toy model’s behavior.
- Empirical calibration of toy parameters: Measure c_min, γ, and α_str on real systems; validate c_fed(N) and the asymmetric α hierarchy; identify domains where federated advantage truly emerges.
- Mapping information gain to utility: Connect I_{1:τ} to task-relevant metrics (prediction accuracy, discovery yield, decision value) to operationalize η for platform design and evaluation.
- Online estimation of τ and <W_t>: Develop methods to estimate/control τ under stochastic <W_t> that depends on policy and state; design stopping rules under diminishing returns and finite budgets.
- Communication channel constraints: Include bandwidth/latency limits for moving Y_t/S_t to archives and between agents; analyze how channel quality constraints reshape H(Y_t) and total energy budgets.
Practical Applications
Immediate Applications
Below are concrete, deployable uses of the paper’s bounds, metric, and strategy comparisons that can be implemented with existing tools and workflows.
- Efficiency benchmarking for automated labs and AI-driven experimentation (industry, academia)
- What to do: instrument platforms to compute information-work efficiency η over rounds; log per-experiment energy and approximate information gain.
- How: estimate per-round mutual information I_t via expected information gain (EIG) from Bayesian experimental design (e.g., BoTorch/Ax, Pyro, Edward2, PyMC) and measure energy/work via power meters on instruments and compute nodes; compute η = I1:τ/(β Wtot).
- Tools/workflows: LIMS/ELN plugins for energy logging; MLOps dashboards that plot η vs budget; “EIG-per-Joule” experiment ranking; early-stopping when marginal η falls below threshold.
- Sectors: materials discovery, biotech, chemistry automation, semiconductor metrology.
- Assumptions/dependencies: tractable MI/EIG approximations; reliable energy telemetry; temperature assumed constant for β; mapping energy≈work.
- Energy-aware experimental design and scheduling (industry, academia)
- What to do: optimize interventions u_t to maximize information gained per joule rather than per trial; prioritize low-entropy-outcome protocols when budgets are tight (budget-limited regime).
- How: use Bayesian optimization targeting objective EIG/energy; schedule batches to maximize cumulative I subject to Wtot; adopt adaptive resolution (e.g., sensor averaging) to reduce H(Yt) where it doesn’t harm I_t materially.
- Sectors: high-throughput screening, A/B testing platforms, field sensing campaigns.
- Assumptions/dependencies: accurate outcome-entropy proxies; ability to trade measurement resolution for energy.
- Protocol and logging optimization to reduce outcome entropy H(Y) (industry, academia)
- What to do: compress outcomes to sufficient statistics S_t (lower H(S_t)); choose sensor settings and preprocessing that reduce redundant entropy without sacrificing informative bits.
- How: lossless compression (e.g., zstd), binning and de-noising, sufficient-statistic extraction, structured logging formats; “reversible” data pipelines that minimize unnecessary erasures.
- Tools/workflows: data schemas emphasizing sufficient statistics; compression profiles per instrument; pre-commit hooks that reject high-entropy-but-uninformative logs.
- Sectors: lab instrumentation, industrial metrology, IoT sensing.
- Assumptions/dependencies: validated sufficiency/adequacy of statistics; compliance with data retention and audit requirements.
- Federated specialization for multi-domain R&D programs (industry consortia, academia)
- What to do: partition the research domain into subdomains K and allocate budgets to subagents to reduce effective prior entropy H(Θ|K); exploit lower overhead in domain-specific modules (lower H(Y) and α).
- How: define K via domain structure or clustering; estimate I(Θ;K) to gauge partition informativeness; allocate Wtot(i) proportionally to p_i and subdomain difficulty; share compressed summaries between modules.
- Sectors: pharma (modality-specific labs), battery materials (cathode/anode/electrolyte lines), advanced manufacturing (process-stage specialization).
- Assumptions/dependencies: clear, informative partitions; governance for data exchange; consistent energy accounting across subagents.
- Active learning and AutoML with “information per joule” objectives (software)
- What to do: select data points/models that maximize MI/energy during training and evaluation; throttle logging and checkpointing to reduce H(Y) overhead in pipelines.
- How: integrate MI/EIG estimators with power monitoring (NVIDIA SMI/Intel RAPL/PDUs); schedule evaluations where MI gain per watt-hour is highest; prefer dataset shards that increase I most per kWh.
- Tools/workflows: Optuna/Ax with custom objective MI/energy; training monitors that report η and its components; data curricula ranked by EIG/kWh.
- Sectors: ML engineering, MLOps, data centers.
- Assumptions/dependencies: MI proxies for complex models (e.g., entropy reduction, BALD); accurate power measurements.
- Energy-normalized metrics in grants and procurement pilots (policy)
- What to do: require reporting of information gain per energy (e.g., η, EIG/kWh) in automated science proposals and progress reports; set procurement guidelines favoring lower H(Y) workflows.
- How: standardized templates for MI estimation and energy logging; review criteria that distinguish prior-limited vs budget-limited regimes.
- Sectors: research funding agencies, university research offices.
- Assumptions/dependencies: community-accepted MI proxies; risk that strict metrics could bias toward short-horizon projects—mitigate with regime-aware evaluation.
- Exploration policies for robots and edge sensors (robotics, energy, environment)
- What to do: select sensing actions that maximize MI per battery joule; compress telemetry to sufficient statistics before transmission; avoid high-entropy logging when it yields little I_t.
- How: embedded EIG estimators for candidate actions; adaptive bitrate and resolution control; on-board summarization S_t.
- Sectors: environmental monitoring, precision agriculture, inspection drones, autonomous vehicles.
- Assumptions/dependencies: real-time MI proxy computation; reliable energy models; mission constraints on compression.
- Teaching and lab-practice updates (academia, daily life)
- What to do: add “information thermodynamics for experiment design” modules; have students log power and compute η for lab exercises; encourage note-taking and learning strategies that maximize information per effort.
- How: course lab kits with smart plugs; Jupyter notebooks computing EIG and η; personal paper planners using info/effort heuristics (e.g., spaced repetition with diminishing-returns stopping rules).
- Sectors: STEM education, edtech, personal productivity.
- Assumptions/dependencies: simple MI proxies (entropy reduction); accessible energy meters.
Long-Term Applications
These opportunities need further research, scaling, hardware advances, or standardization to realize.
- Thermodynamically optimized autonomous science platforms (industry, academia)
- Vision: closed-loop robotic scientists that schedule experiments by maximizing I per joule across federated modules, adapting K dynamically as understanding evolves.
- Required advances: reliable on-line MI estimation at scale, cross-platform energy telemetry, orchestration that tracks η and regime transitions, robust inter-module compression.
- Sectors: automated discovery platforms, contract research networks.
- Dependencies: interoperable metadata standards; incentives for data sharing; safety and validation frameworks.
- Reversible/low-dissipation computing and memory for lab automation (hardware)
- Vision: controllers, data paths, and storage that minimize erasure cost, approaching Landauer limits and reducing ΔFmem penalties.
- Required advances: reversible logic circuits, adiabatic computing, non-volatile memories with low-energy erase/write, sensor front-ends with tunable entropy.
- Sectors: semiconductor, instrumentation, edge AI hardware.
- Dependencies: manufacturable processes; software stacks that exploit reversibility; cost–benefit validation.
- Standardization of “Joules per bit of discovery” and carbon accounting (policy, finance)
- Vision: sector-wide metrics for information productivity (η, EIG/kWh), tied to sustainability disclosures and funding decisions; possible carbon credits for efficiency gains.
- Required advances: consensus MI proxies per field; audit methods for energy logs; benchmarks across regimes (prior-limited vs budget-limited).
- Sectors: funding agencies, journals, ESG reporting, insurers.
- Dependencies: community governance; avoidance of metric gaming; treatment of qualitative breakthroughs.
- National/international federated research networks (policy, academia, industry consortia)
- Vision: multi-node platforms partitioning domains (K) across specialized sites with coordinated budgets Wtot(i), sharing compressed information reservoirs to lower H(Θ|K) and α.
- Required advances: secure, low-entropy data exchange; cross-institution η dashboards; dynamic partition learning via I(Θ;K).
- Sectors: health, energy materials, climate science.
- Dependencies: legal data-sharing frameworks; equitable credit allocation; cybersecurity.
- Energy-aware clinical diagnostics and triage (healthcare)
- Vision: test sequences and imaging protocols optimized for information per joule and patient/time budgets; federated clinics specializing by modality to reduce overhead.
- Required advances: MI estimation for diagnostic tests; outcome entropy control via acquisition protocols; integration with EHRs and power telemetry.
- Sectors: radiology, lab medicine, telehealth.
- Dependencies: regulatory approval; patient safety constraints; fairness and access considerations.
- Grid, climate, and subsurface monitoring with MI/J planning (energy, environment)
- Vision: sensing campaigns that schedule measurements by MI per field energy cost (truck rolls, drone flights), with on-board compression and federated analysis.
- Required advances: field-deployable MI estimators; robust telemetry compression preserving sufficiency; joint budget- and prior-limited planning at scale.
- Sectors: utilities, oil & gas, environmental agencies.
- Dependencies: ruggedized hardware; variable environmental “temperature” analogs (operational conditions).
- Mission planning for space exploration (aerospace, robotics)
- Vision: rover/orbiter action selection maximizing information per joule under severe energy constraints; federated instruments specialized by target geology/atmosphere.
- Required advances: low-power MI estimation; extreme compression pipelines; fault-tolerant reversible storage.
- Dependencies: radiation-hardened hardware; long-latency autonomy.
- Portfolio optimization of R&D by η and regime (finance, corporate strategy)
- Vision: allocate capital across programs using expected η, distinguishing prior-limited (knowledge-rich) vs budget-limited (energy-constrained) lines to avoid diminishing returns.
- Required advances: program-level MI modeling; standardized energy accounting; risk-adjusted η forecasts.
- Dependencies: organizational adoption; data confidentiality; outcome valuation frameworks.
- Adaptive learning platforms maximizing “information per effort” (education, edtech)
- Vision: curricula and tutors that schedule items to maximize MI per minute/cognitive load; compress feedback to sufficient statistics; energy-aware data collection in A/B testing.
- Required advances: MI proxies for learning outcomes; models of effort/energy; privacy-preserving compression.
- Dependencies: ethical data use; accessibility; alignment with pedagogy.
- Foundation-model training and fine-tuning with MI/energy governance (software, AI)
- Vision: select pretraining corpora and fine-tuning batches by marginal MI per kWh; federated training where domain partitions lower effective prior and overhead.
- Required advances: scalable MI estimators for large models (e.g., entropy reduction surrogates); precise power telemetry in distributed training; reversible logging/checkpointing.
- Dependencies: framework support (PyTorch/JAX) for energy-aware schedulers; datacenter cooperation.
Cross-cutting assumptions and dependencies
- Physical idealizations: the bounds treat ΔFmem≈0 and often assume storing full Y_t; real hardware may incur additional costs or benefit from better compression than the baseline bounds.
- Estimating information terms: exact I_t and H(Y_t) are often intractable; practical proxies include entropy reduction of predictive posteriors, BALD, Fisher information, or variational estimates.
- Energy/work measurement: requires reliable power telemetry and consistent mapping from energy to “work” per the model; ambient temperature T should be recorded for β if needed.
- Strategy selection: federated advantages rely on informative partitions (I(Θ;K)>0) and reduced outcome entropy (αfed<αgen); otherwise, generalists can dominate under matched budgets.
- Governance and incentives: meaningful adoption in policy and consortia needs standards, auditability, and safeguards against metric gaming.
Glossary
- Budget–information tradeoff: A fundamental relation showing how the amount of learnable information is limited by the available thermodynamic work and outcome entropy. "Together with \eqref{eq:telescoping} we obtain the fundamental budget–information tradeoff for any unpartitioned strategy:"
- Budget-limited regime: The regime where learning is constrained by the available work rather than the prior uncertainty. "Budget-limited: $\beta W_{\mathrm{tot} \ll H(\Theta_0)$ is capped by the work budget and further reduced by the sum of the outcome entropies."
- Chain rule for entropy: A property of entropy that decomposes joint uncertainty into conditional pieces; used to compare partitioned and unpartitioned priors. "By the chain rule for entropy,"
- Conditional prior: A prior distribution over states given a subdomain or condition, reflecting remaining uncertainty within that segment. "the conditional prior over the same underlying state "
- Degenerate prior: A prior concentrated entirely on a single outcome or subdomain, eliminating uncertainty about which subdomain is active. "but a degenerate prior"
- Entropy-compression factor: A parameter measuring how much effective prior entropy is reduced by strategy or partitioning. "the entropy-compression factor $c_{\mathrm{str}$ becomes increasingly important."
- Epistemic uncertainty: Uncertainty in knowledge about the environment or state, which research aims to reduce. "interacting with an environment to reduce epistemic uncertainty."
- Federated specialization: A strategy that partitions tasks across specialized subdomains; becomes advantageous when it reduces both prior and outcome entropies. "Federated specialization becomes thermodynamically advantageous when it simultaneously reduces the effective entropy of the domain and the outcome entropy of the measurement process."
- Federated strategy: An approach that partitions the environment into subdomains with separate work allocations and conditional priors. "A federated strategy partitions the environment into subdomains, indexed by a discrete random variable "
- Helmholtz free energy: A thermodynamic potential that quantifies usable work in systems at constant temperature and volume; here, the change in memory’s physical state. "the change in Helmholtz free energy of the physical memory used to store the outcome at round "
- Information reservoir: An idealized storage medium whose free energy change is negligible, enabling analysis focused on informational costs. "We idealize this archive as an information reservoir with negligible change in free energy over the rounds"
- Information thermodynamics: The paper of energetic costs associated with information processing and acquisition in physical systems. "Information thermodynamics provides rigorous lower bounds on the energetic cost of information acquisition"
- Information–work efficiency: A scale-free metric quantifying information gained per unit of thermodynamic work invested. "For any strategy, define the scale-free information-work efficiency after rounds and total invested work $W_{\mathrm{tot}$:"
- Inverse temperature (β): The reciprocal of thermal energy scale, linking temperature to work/entropy in thermodynamic bounds. "$\beta \equiv (k_B T)^{-1$."
- Irreversibility penalty: The efficiency loss due to non-reversible measurement and erasure processes, modeled as an overhead in efficiency. "a dimensionless measure of the outcome-entropy contribution and irreversibility penalty"
- Landauer bound: The minimum thermodynamic work required to erase information, proportional to the memory’s entropy. "Equation~\eqref{eq:erase-step} is the Landauer bound for erasing a memory with Shannon entropy $H(Y_t^{\mathrm{mem})$."
- Latent environment state: The unobserved true state of the environment that the agent seeks to infer via measurements. "Let denote the latent environment state with prior "
- Measure–update–erase cycle: The repeated operational loop: measure outcomes, update beliefs, and erase memory, each with associated work costs. "Each round is defined as a measure–update–erase cycle on a working memory or register."
- Mutual information: The information gained about the environment state from an outcome, conditioned on past observations and controls. "One can write the mutual information contributed at round (conditioned on the history) as"
- Outcome entropy: The entropy of measurement outcomes (or their stored representation), which determines erasure cost and contributes to work. "recognizing the nonnegativity of outcome entropy "
- Outer-product structure: A sparse combinatorial structure where variables factorize, allowing substantial entropy reduction via partitioning. "In a heterogeneous domain with sparse outer-product structure (suggesting a highly non-uniform density of state)"
- Partition variable: A random variable indicating which subdomain is active, enabling federated decomposition of the environment. "Introducing a partition variable shows how strategic choices enter the bounds through two quantities"
- Prior entropy: The uncertainty in the environment state before any measurements; effective versions differ across strategies. "the effective prior entropy (e.g.\ $H_{\mathrm{gen}$, $H_{\mathrm{fed}$)"
- Prior-limited regime: The regime where learning is limited by remaining prior uncertainty rather than available work. "Prior-limited: $\beta W_{\mathrm{tot} \gg H(\Theta_0)$ saturates at (no more learnable information remains)."
- Redundancy (information theory): The superfluous part of stored outcomes beyond a compressed statistic, which need not be erased. "the redundancy would not contribute to the erasure cost."
- Reversible measurement: An idealized measurement with no excess work beyond free-energy changes; unattainable in practice. "with equality only in the unphysical limit of both vanishing outcome entropy and a reversible measurement."
- Sequential Bayesian learning: Iterative updating of beliefs over rounds of measurement and control under a probabilistic model. "bounds on information gain over rounds of sequential Bayesian learning."
- Thermodynamics of computing: The physics-based framework quantifying energetic limits of computation and information processing. "Using established results about the thermodynamics of computing, we derive finite-budget bounds on information gain"
- Work budget: The total available thermodynamic work allocated across rounds, constraining achievable information gain. "Assume a fixed total work budget $W_{\mathrm{tot}$ allocated across rounds"
Collections
Sign up for free to add this paper to one or more collections.