The Path Not Taken: RLVR Provably Learns Off the Principals (2511.08567v1)
Abstract: Reinforcement Learning with Verifiable Rewards (RLVR) reliably improves the reasoning performance of LLMs, yet it appears to modify only a small fraction of parameters. We revisit this paradox and show that sparsity is a surface artifact of a model-conditioned optimization bias: for a fixed pretrained model, updates consistently localize to preferred parameter regions, highly consistent across runs and largely invariant to datasets and RL recipes. We mechanistically explain these dynamics with a Three-Gate Theory: Gate I (KL Anchor) imposes a KL-constrained update; Gate II (Model Geometry) steers the step off principal directions into low-curvature, spectrum-preserving subspaces; and Gate III (Precision) hides micro-updates in non-preferred regions, making the off-principal bias appear as sparsity. We then validate this theory and, for the first time, provide a parameter-level characterization of RLVR's learning dynamics: RLVR learns off principal directions in weight space, achieving gains via minimal spectral drift, reduced principal-subspace rotation, and off-principal update alignment. In contrast, SFT targets principal weights, distorts the spectrum, and even lags RLVR. Together, these results provide the first parameter-space account of RLVR's training dynamics, revealing clear regularities in how parameters evolve. Crucially, we show that RL operates in a distinct optimization regime from SFT, so directly adapting SFT-era parameter-efficient fine-tuning (PEFT) methods can be flawed, as evidenced by our case studies on advanced sparse fine-tuning and LoRA variants. We hope this work charts a path toward a white-box understanding of RLVR and the design of geometry-aware, RLVR-native learning algorithms, rather than repurposed SFT-era heuristics.
Sponsor
Summary
- The paper demonstrates that RLVR achieves high reasoning performance by concentrating updates in low-curvature, off-principal subspaces.
- It reveals that update sparsity is driven by bfloat16 precision and model geometry rather than gradient decay, confirmed by consistent banding patterns.
- The study introduces the Three-Gate Theory, linking KL anchors, structured model geometry, and precision filtering to explain spectrum-preserving weight updates.
RLVR Optimization Geometry: Off-Principal Update Dynamics in LLM Reasoning
Overview and Motivation
This work addresses a persistent paradox in RL-based fine-tuning of LLMs: Reinforcement Learning with Verifiable Rewards (RLVR) consistently improves LLM reasoning quality while modifying only a small fraction of parameters compared to Supervised Fine-Tuning (SFT). The paper provides a parameter-space characterization and mechanistic explanation for RLVR’s distinctive update regime, arguing that this apparent sparsity is not a fundamental property but a superficial artifact of a deeper, geometry-driven optimization bias. The core thesis is that RLVR updates are concentrated in low-curvature, spectrum-preserving subspaces, consistently routed away from principal directions, with these dynamics invariant to choice of dataset and RL algorithm but highly sensitive to pretrained model geometry.
Empirical Analysis of RLVR Update Patterns
The paper presents robust empirical evidence showing that RLVR modifies only a small, stable subset of weights across several open LLM checkpoints, with update sparsity for RL ranging from 36% to 92%, compared to SFT’s 0.6% to 18.8%. Crucially, the positions of updated weights show high cross-run consistency and clear contiguous banding within projection matrices, visualized through consensus maps and Jaccard similarity scores.
Figure 1: RLVR weight updates concentrate in stripe-like, stable bands, invariant across runs, indicating a robust model-conditioned optimization bias.
Temporal analysis demonstrates early emergence and ongoing reinforcement of this routing pattern throughout training, with similar structures observed in unrelated model families (Llama and Mistral), confirming its generic nature.
Notably, sparsity is shown to be mainly a consequence of bfloat16 precision suppressing sub-ULP (unit-in-last-place) micro-updates in non-preferred regions, not a result of gradient vanishing or zero learning rates. Increasing the learning rate or switching to float32 removes the sparse signature but does not improve downstream performance, cementing interpretation of sparsity as an epiphenomenon of geometry-aligned optimization bias.
Three-Gate Theory: Mechanistic Explanation for RLVR Updates
The authors introduce the Three-Gate Theory as a mechanistic account of RLVR’s optimization regime:
- Gate I (KL Anchor): On-policy RL algorithms (e.g., PPO, GRPO, DAPO) enforce a per-step policy KL constraint, tethering each update to remain close to the reference policy, even in algorithms without explicit KL penalties due to ratio clipping.
- Gate II (Model Geometry): Pretrained model weight matrices exhibit highly structured geometry, with principal weights representing high-curvature, high-energy directions. Under the KL leash, RLVR steps are steered into low-curvature subspaces away from these principal directions, resulting in spectrum- and subspace-preserving updates that conserve the top-k singular vectors and values.
- Gate III (Precision Filter): Finite precision (bfloat16) hides micro-updates in non-preferred regions, making the off-principal bias appear as sparsity.
This framework is mathematically grounded, leveraging layerwise Fisher information bounds, singular value perturbation theory, and principal subspace rotation metrics to bound spectral drift under RLVR optimization.
Figure 2: SFT traverses high-curvature, principal directions in parameter space, while RLVR, steered by the model’s geometry and KL constraint, takes spectrum-preserving detours through low-curvature regions.
Spectral Characterization: RLVR Preserves Model Structure
Spectral analysis across model families reveals that RLVR leaves layer singular-value spectra and top-k principal subspaces nearly unchanged, in stark contrast to SFT, which induces much larger subspace rotations and eigenvalue drifts.
Figure 3: RLVR exhibits minimal principal subspace rotation and spectral drift compared to SFT, consistent with the low-curvature update regime.
Micro-level analysis shows that RLVR avoids updating principal weights, defined as the largest-magnitude entries in a rank-k SVD reconstruction, preferring instead low-magnitude, non-principal regions. The overlap between RLVR update masks and principal masks is systematically sub-random, while overlap with low-magnitude regions is super-random, confirming strong directional selectivity.
Figure 4: RLVR updates show negative correlation with principal weights, and positive correlation with low-magnitude regions, indicating geometry-driven routing.
Interventional studies further support the causal link: function-preserving orthogonal rotations or head permutations of weights disrupt RLVR’s optimization bias, reducing update overlap to random levels only in manipulated layers, while intact layers retain deterministic routing.
Generality Across Agents and RLHF
The off-principal, spectrum-preserving signatures of RLVR extend to agentic tasks (multi-turn planning, tool use) and RL with Human Feedback (RLHF), regardless of domain, reward signal, or model family.
Figure 5: RL-trained agents show robust misalignment between update masks and principal weights, maintaining off-principal bias in agentic settings.
Figure 6: Across agent and RLHF checkpoints, RLVR preserves layer spectra and principal subspaces, confirming the regime’s generality.
Design Implications: Reorienting PEFT for RLVR
The findings have direct implications for Parameter-Efficient Fine-Tuning (PEFT):
- Sparse fine-tuning targeting principal weights reproduces SFT update geometry and yields suboptimal trajectories in RLVR (slow KL drift, lower reasoning accuracy).
- Masks that exclude principal weights and favor low-magnitude, non-principal regions allow sparse RLVR runs to closely track full-parameter performance (using ~70% of weights), confirmed by final metrics.
- Low-rank adapters align with the RLVR regime only when they capture the effective, off-principal subspace, while principal-targeted adapter variants (e.g., PiSSA) fail to confer gains and destabilize optimization at higher learning rates.
These results collectively underscore a bold claim: directly repurposing SFT-era sparse and low-rank PEFT methods for RLVR is fundamentally flawed; successful RLVR post-training requires geometry-aware, RL-native parameter selection.
Theoretical and Practical Implications
The paper advances a white-box understanding of RLVR’s parameter evolution, linking macroscopic spectral stability to microscopic routing bias mediated by model geometry and KL constraints. In practice, RLVR allows highly targeted weight updates, greatly reducing the redundancy and computational overhead associated with dense parameter-space exploration. The Three-Gate framework sets the stage for future development of geometry-adaptive RL optimizers and masking schedules, potentially enabling more efficient post-training even in resource-constrained contexts.
On the theoretical front, the findings clarify the distinction between externally guided optimization (SFT) versus compass-like, model-steered RL, providing a rigorous basis for the observed generalization and robustness of RLVR-tuned models. They further suggest that diagnostic probes for model updating should shift focus from raw sparsity metrics to more nuanced geometric and spectral signatures.
Conclusion
This paper provides a rigorous parameter-level account of RLVR’s optimization dynamics, resolving the paradox of visible sparsity and demonstrating that RLVR learns via stable, off-principal, spectrum-preserving paths dictated by pretrained model geometry. Existing SFT-based PEFT heuristics do not transfer; instead, practical RLVR requires geometry-aware masks tuned to the model’s latent structure. These insights facilitate principled advances in efficient RL-based reasoning model post-training and broaden the theoretical toolkit for analyzing and engineering LLM optimization.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview of the paper
This paper studies how a training method called “Reinforcement Learning with Verifiable Rewards” (RLVR) improves the reasoning of LLMs. RLVR rewards the model for producing answers that are easy to check, like correct math solutions or code that runs. The surprising part: RLVR makes models much smarter while apparently changing only a small part of their internal settings (their “weights”). The authors explore this puzzle and explain what’s really happening inside the model during RLVR.
What questions are they asking?
The paper asks two big questions in simple terms:
- Why does RLVR seem to change so few model weights even though it uses a lot of compute?
- Where do those changes happen inside the model, and what rules or “bias” guide them?
How did they paper it? Methods and key ideas explained
The authors look inside different trained models, comparing their weights before and after RLVR. They track which parts change, how much the model’s “shape” changes, and whether the same places change across different runs and datasets. They also compare RLVR to another method called Supervised Fine-Tuning (SFT), where a model learns by copying a teacher’s answers.
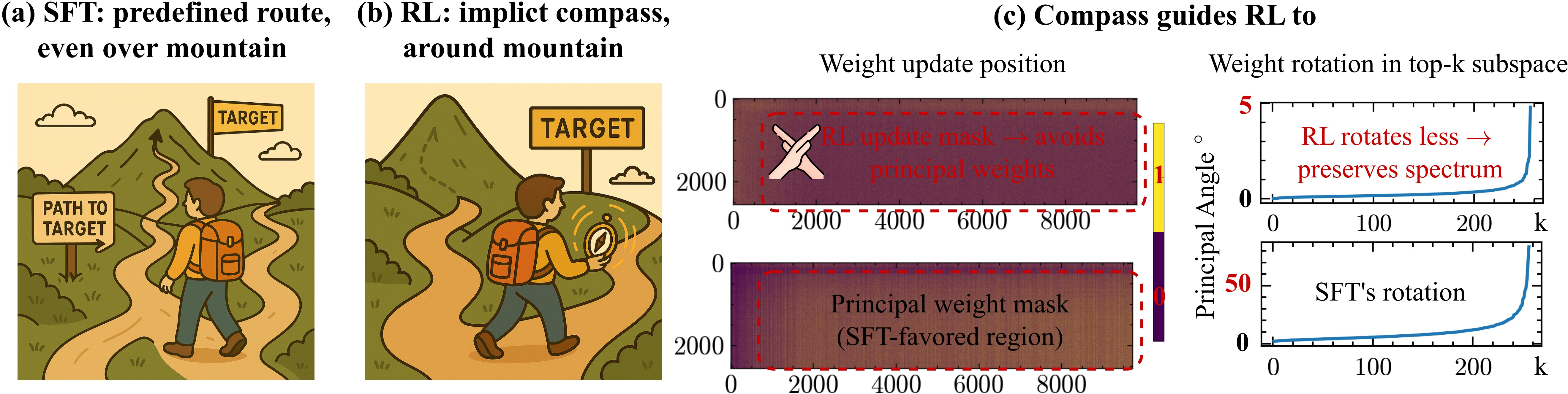
To explain their findings, they propose the “Three-Gate Theory.” Think of training like hiking over a mountain to reach better performance. SFT takes a teacher-led path straight over the mountain (steep and direct). RLVR uses a built-in “compass” and prefers smoother detours around steep slopes.
What is RLVR and SFT?
- RLVR: The model tries answers and gets a simple, verifiable reward (e.g., “pass/fail” for math or code). It learns by nudging its behavior toward higher rewards.
- SFT: The model is trained to match a set of correct answers from a teacher, usually changing weights more directly and widely.
The Three-Gate Theory (with everyday analogies)
- Gate I: KL Anchor (a safety leash)
- Analogy: A dog on a short leash can’t run far from its owner. In RLVR, each training step includes a kind of “distance limit” (called KL) that prevents the model’s behavior from drifting too far from where it started. This keeps changes small each step.
- Gate II: Model Geometry (the terrain shapes the path)
- Analogy: A well-built machine has strong main gears and many smaller parts. Pushing on main gears can cause big, risky changes; pushing on smaller parts can make fine adjustments. The “geometry” of a pretrained model has “principal directions” (its strongest pathways) and gentler directions. RLVR’s leash and the model’s terrain steer updates away from those strong principal directions into smoother, low-curvature directions. This preserves the model’s internal structure while still improving performance.
- Gate III: Precision (what you can see depends on your camera)
- Analogy: If your camera is low-resolution, tiny changes don’t show up. Many RLVR updates are very small. Because weights are stored in a format with limited precision (called “bfloat16”), tiny changes may get rounded away and look like “no change.” So the apparent “sparsity” (few changes) is partly a visibility issue, not that nothing happened.
Technical terms in simple language
- KL (Kullback–Leibler) “distance”: A way to measure how different a model’s new behavior is from its old behavior. RLVR keeps this small each step.
- Principal directions/weights: The model’s strongest, most influential pathways—like the main beams of a bridge. Changing them can have big effects.
- Low curvature: Directions where a small change doesn’t cause big swings—like taking a gentle slope around a hill instead of a steep climb.
- bfloat16 precision: A storage format that saves memory but can’t represent very tiny changes, making small updates hard to see.
- Spectrum and subspace rotation: Ways to describe the model’s internal shape. If the spectrum stays similar and subspaces don’t rotate much, the model’s core structure is preserved.
- RLHF (Reinforcement Learning with Human Feedback): Similar to RLVR, but rewards come from human preferences instead of automatically verifiable checks.
What did they find and why is it important?
The authors run many tests across different models, tasks, and RL variations. Here are the key findings:
- RLVR changes are real, but they look sparse because of precision: Many RLVR updates are tiny and get hidden by the bfloat16 format. If you use higher precision or slightly scale the updates, the “sparsity” mostly disappears.
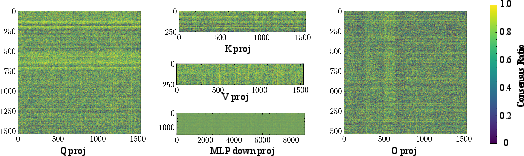
- The updates follow a consistent, model-specific pattern: For a given base model, RLVR tends to change the same regions across different runs and datasets. The update “footprints” show stripe-like bands, not random scatter. This means the model’s own structure guides where RLVR makes changes.
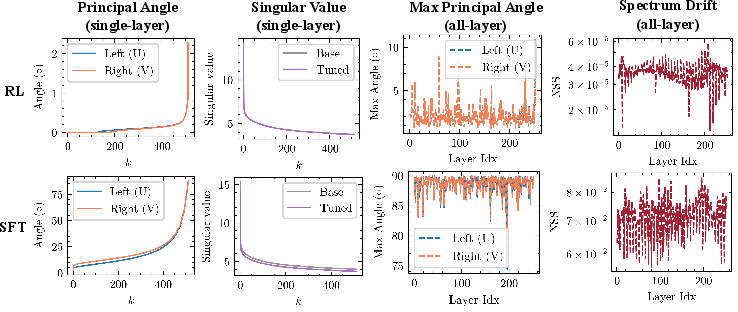
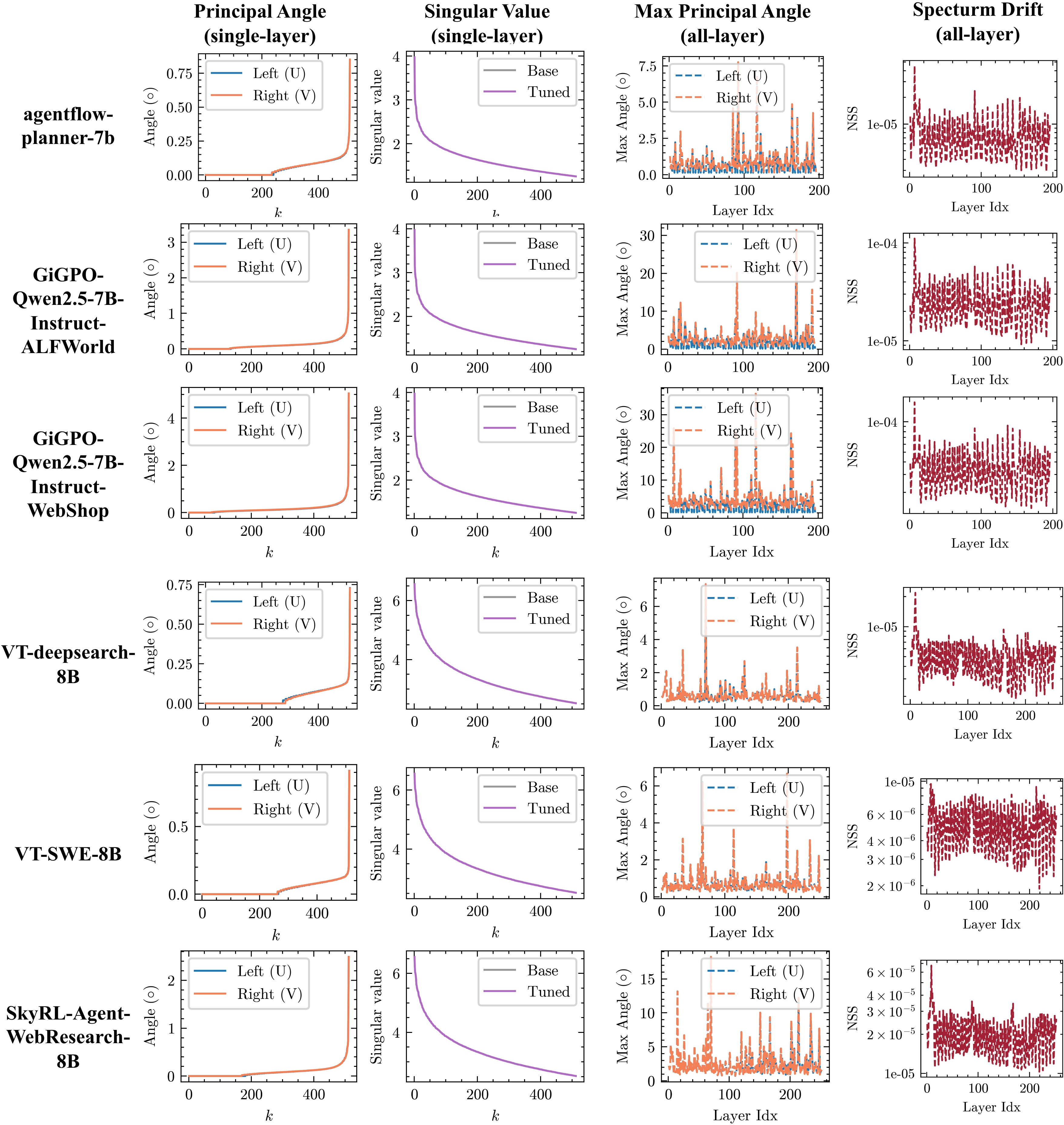
- RLVR preserves the model’s internal shape: Compared to SFT, RLVR causes minimal rotation of the model’s main subspaces and very little shift in the spectrum. In plain terms, RLVR improves performance while keeping the model’s core geometry intact.
- RLVR avoids principal weights; SFT targets them: RLVR mainly updates smaller, non-principal weights (gentler directions). SFT tends to push on principal weights (strong directions), which can distort the model’s structure more.
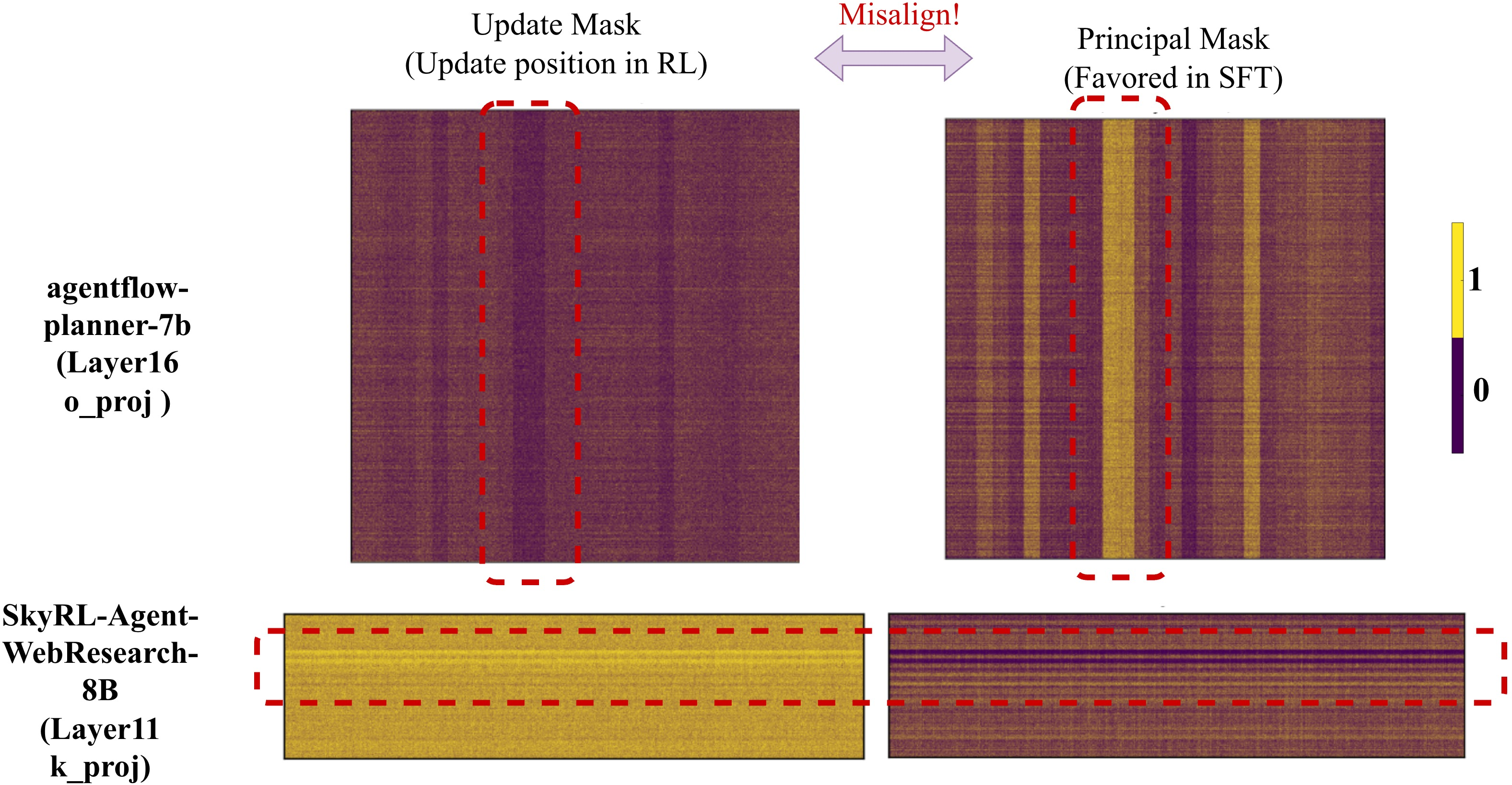
- If you scramble the model’s geometry, RLVR’s update pattern disappears: When the authors “rotate” or permute parts of the model (without changing its function), the consistent update overlap collapses to random. This shows the model’s geometry is the source of RLVR’s routing bias.
- The same RLVR signature shows up in agents and RLHF: In long, multi-step tasks (like web research, planning, or tool use) and in RLHF-trained models, the same pattern appears—stable spectra, minimal rotation, and off-principal updates.
Why it matters: This explains why RLVR can deliver big reasoning gains without heavily rewriting the model. It also shows that RLVR operates in a different training regime than SFT—guided by a model-conditioned bias and a KL leash—so we shouldn’t assume techniques that work for SFT will work for RLVR.
What could this change or lead to?
This work suggests a shift in how we design fine-tuning methods for reasoning models:
- Don’t blindly reuse SFT-era tricks: Some parameter-efficient fine-tuning (PEFT) methods that focus on principal weights (like certain LoRA variants designed for SFT) are misaligned with RLVR. They push on the wrong parts of the model for RL-style training and can harm stability or performance.
- Build RLVR-native, geometry-aware methods: Since RLVR learns “off the principals,” new techniques should respect the model’s geometry, the KL leash, and the precision reality. That could mean targeting low-curvature, non-principal directions and designing adapters or schedules that preserve the spectrum.
- A clearer, “white-box” understanding of RLVR: Instead of treating RL as a black box, this paper offers a parameter-level view of how RLVR changes models. That can help researchers debug training, predict behavior, and make smarter choices about where and how to update weights.
In short, RLVR doesn’t win by brute force. It makes careful, targeted changes in the model’s gentler directions, keeps the overall structure steady, and uses a consistent, model-shaped path to improve reasoning—an approach that calls for new, RL-specific fine-tuning methods.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a concise list of concrete gaps and open questions that remain unresolved and could guide future research:
- Generalization across scales and architectures: Validate the Three-Gate Theory on substantially larger LRMs (e.g., 30B–70B, o3/R1-scale) and diverse architectures (e.g., deeper MoEs, decoder-only vs encoder–decoder) beyond the Qwen/Mistral/Llama family used here.
- Multi-step theory: Extend Gate I’s one-step KL leash to a rigorous multi-step analysis that bounds cumulative spectral drift and subspace rotation over long-horizon RLVR training.
- Practical KL quantification: Systematically measure the per-step and cumulative policy KL across PPO/GRPO/DAPO/Reinforcement++ under typical hyperparameters to test the “small-step” assumption and quantify how clipping and β schedules actually enforce the leash.
- Curvature verification: Directly estimate per-layer curvature (e.g., Fisher/Hessian diagonals or block approximations) to confirm that RLVR updates follow low-curvature directions rather than relying solely on principal-weight proxies.
- Principal-weight proxy robustness: Assess sensitivity of the principal-weight mask to choices of SVD rank k and selection fraction α; compare against alternative proxies (e.g., Fisher eigenvectors, NTK directions) to verify high-curvature correspondence.
- Coverage of non-linear and non-weight parameters: Examine whether avoidance of principal directions extends to attention biases, LayerNorm scales/shifts, routing/gating parameters, and embedding matrices; current analysis focuses on weight matrices.
- MoE-specific dynamics: Quantify update localization across experts (shared vs expert-specific weights), router behavior, and expert activation patterns to determine whether off-principal routing holds uniformly in MoEs.
- Precision gate rigor: Conduct controlled experiments across bf16, fp16, and fp32 (and with/without dynamic loss scaling) to isolate precision effects on apparent sparsity, update magnitudes, and task performance.
- Micro-update distribution: Characterize the distribution of update magnitudes relative to bf16 ULP thresholds and track how often sub-ULP updates occur per layer/head; connect this to sparsity emergence over time.
- Causal performance link: Perform counterfactual training that constrains updates to principal vs non-principal regions (with matched compute and stability) to causally test whether off-principal routing drives reasoning gains.
- Reward and data dependence: Stress-test the “model-conditioned, data-invariant” bias across reward shapes (binary, continuous, dense), domains (beyond math/code/agents), and exploration settings (temperature, top-p) to determine boundary conditions.
- Hyperparameter sensitivity: Map how LR, β, clip ranges, batch sizes, gradient clipping, and optimizer choices (AdamW/Adafactor) modulate spectral drift, subspace rotation, and update localization.
- Rotation/permutation interventions at scale: Expand function-preserving interventions (orthogonal rotations, head permutations) to many layers and models; verify function preservation empirically and quantify the resulting update-overlap collapse and performance impact.
- SFT–RLVR interaction: Investigate how different SFT stages (objectives, datasets, durations) shape the pretrained geometry and whether certain SFT regimes precondition models for more favorable RLVR dynamics.
- LoRA mechanism analysis: Measure alignment of LoRA update subspaces (rank, init, scaling) with principal vs off-principal directions; explain why PiSSA’s principal-targeting helps SFT but not RLVR; seek principled criteria for RL-native adapter design.
- RL-native PEFT algorithms: Design and evaluate geometry-aware PEFT that explicitly targets off-principal, low-curvature, low-magnitude regions (e.g., adaptive masks/adapters) and compare against dense RLVR baselines on stability and performance.
- Predictive geometry metrics: Identify actionable geometry indicators (e.g., thresholds on spectral drift, principal-angle rotation) that predict RLVR stability/performance and can be used to tune training or early-stop.
- Temporal coupling: Link the emergence of stripe-like update locality to learning curves (rewards/KL/accuracy), exploring whether update patterns can serve as early signals of training success or collapse.
- Safety and side-effects: Assess whether off-principal updates inadvertently alter non-reasoning behaviors (toxicity, instruction-following, safety alignment), given the claim of minimal spectral drift.
- Post-training quantization: Examine whether off-principal updates are robust to post-training quantization/compression and whether geometry signatures survive deployment constraints (e.g., int8 quantization).
- Tokenization and sequence-length effects: Analyze how CoT length, prompt formatting, and tokenization choices influence curvature, principal subspaces, and update routing.
- Statistical robustness: Provide broader cross-seed statistics (beyond exemplar layers) and confidence intervals for Jaccard overlaps, consensus ratios, and overlap baselines to rule out layer-specific artifacts.
- Theory–practice gap in Gate I: Derive bounds connecting the M-projection idealization to actual PPO/GRPO/DAPO implementations (with clipping, advantage normalization, entropy bonuses), clarifying when the implicit KL leash holds tightly.
- Incompleteness of Section 6: The paper signals a rethinking of RL-native PEFT but does not present concrete algorithms or comprehensive empirical evaluations; a full design–test cycle remains to be done.
Practical Applications
Immediate Applications
The following applications can be deployed now by practitioners and researchers, leveraging the paper’s validated findings and tools to make RLVR training more stable, interpretable, and cost‑effective.
- Geometry‑aware RLVR diagnostic suite for training and MLOps
- Sectors: software/ML infrastructure, enterprise AI, academia
- What: Add “geometry dashboards” during RLVR runs that track principal‑subspace rotation, normalized spectral drift, update–principal overlap, and bf16-aware sparsity measures to gate training and catch instability early.
- Tools/Workflows: SVD per layer to compute principal angles; Ky Fan norms; bf16-aware unchanged‑weight probe; consensus update maps; layer/head‑level routing heatmaps.
- Benefits: Early detection of collapse when enforcing principal updates; spectrum‑preserving progress monitoring; reproducible RLVR runs across seeds/datasets.
- Assumptions/Dependencies: Access to model weights; per‑layer SVD feasible at scale; mixed‑precision settings known; RL frameworks (e.g., verl) expose hooks; verifiable rewards used.
- RLVR‑native fine‑tuning recipe for enterprise LLMs (off‑principal targeting)
- Sectors: software, finance, healthcare, education
- What: Prefer updates in low‑curvature, non‑principal, low‑magnitude weights; avoid principal‑targeted sparse/low‑rank methods (e.g., PiSSA‑aligned adapters).
- Tools/Workflows: Mask updates to low‑magnitude entries; orient LoRA toward off‑principal directions; moderate learning rates to respect the KL leash; avoid LR scaling designed to force principal updates; track forward‑KL drift.
- Benefits: Improved reasoning gains with minimal spectral drift; reduced catastrophic forgetting and better retention of base capabilities; stable training in agents and RLHF.
- Assumptions/Dependencies: Pretrained geometry is intact; rewards are verifiable; KL regularization or clipping is present; adapter orientation configurable.
- Bfloat16‑aware instrumentation to correctly read “sparsity” and avoid misdiagnosis
- Sectors: ML infrastructure, enterprise AI
- What: Use bf16‑aware equality thresholds (ULP‑based) to distinguish genuine unchanged weights from micro‑updates hidden by precision; optionally store critical layers in float32 for validation.
- Tools/Workflows: Magnitude‑dependent comparison with η≈1e−3; precision‑aware logging; selective float32 checkpoints for audit layers.
- Benefits: Prevents false conclusions about “zero gradients”; clarifies that visible sparsity is a precision‑amplified readout of an optimization bias, not the underlying cause.
- Assumptions/Dependencies: Mixed precision (bf16 compute, fp32 optimizer states); access to raw weights; training telemetry.
- RLHF and agent training stabilization via spectrum preservation gates
- Sectors: agents/tool‑use platforms, customer support, SWE automation, web research tools
- What: Apply geometry checks (principal angles, drift) to RLHF and agent RL runs to reduce unintended behavior changes and preserve base capabilities while adding task‑specific skills.
- Tools/Workflows: Integrate geometry dashboards in GRPO/DAPO/DPO/SimPO pipelines; gate promotions to production on low drift/rotation; enforce KL budgets per layer.
- Benefits: More reliable multi‑turn agents and tool users; fewer regressions in general knowledge while improving reasoning/task performance.
- Assumptions/Dependencies: Reward shaping and KL/clipping present; access to base and finetuned checkpoints; per‑layer metrics computed regularly.
- PEFT portfolio triage: prefer standard LoRA over principal‑aligned variants for RLVR
- Sectors: software, enterprise model ops
- What: Choose standard low‑rank adapters and avoid principal‑targeted variants (e.g., PiSSA) in RLVR, since principal‑direction enforcement can destabilize training and shows no clear gains.
- Tools/Workflows: Maintain moderate ranks (even rank‑1 viable); orient adapters away from top‑k principal directions; monitor collapse signals when LR scaling is applied.
- Benefits: Matches full‑parameter RL performance more safely; reduces tuning cycles and failures.
- Assumptions/Dependencies: Adapter orientation controllable; runtime allows layerwise metrics; KL leash respected.
- Compliance and governance checks using KL‑anchored drift limits
- Sectors: policy/regulation, enterprise risk, safety
- What: Require per‑step and cumulative KL drift reporting and spectrum‑preservation metrics in RL post‑training as part of model governance and release criteria.
- Tools/Workflows: KL budget schedules; drift thresholds; audit logs linking geometry metrics to training decisions.
- Benefits: Safer deployment; traceable reasoning improvements; white‑box accountability for model changes.
- Assumptions/Dependencies: Regulatory buy‑in; standardized telemetry; verifiable reward pipelines.
Long‑Term Applications
The following opportunities require further research, scaling, or productization to fully realize their impact but are directly informed by the paper’s Three‑Gate Theory and empirical signatures.
- RLVR‑native, geometry‑aware PEFT families and optimizers
- Sectors: software, ML infrastructure
- What: Design adapters and optimizers that explicitly steer updates into low‑curvature, off‑principal subspaces while preserving the spectrum (e.g., off‑principal LoRA, spectrum‑regularized RL optimizers, layerwise KL budgets).
- Potential Products: “Compass‑guided RL” libraries; spectrum‑preserving adapters; per‑layer KL schedulers.
- Assumptions/Dependencies: Robust proxies for curvature; scalable SVD or learned geometry estimators; adapter orientation control.
- Automated “update atlas” of model‑conditioned routing bias
- Sectors: MLOps, foundation model providers
- What: Build per‑model maps of stable update locality (stripe patterns, head‑specific bands) to accelerate safe fine‑tuning and personalization.
- Potential Products: Update locality registries; routing‑aware fine‑tuning planners; seed‑robust tuning profiles.
- Assumptions/Dependencies: Consistency across versions; tooling to capture consensus maps; portability across model sizes and families.
- Personalization with minimal forgetting via off‑principal RL
- Sectors: consumer assistants, enterprise copilots, education
- What: Use off‑principal RL to add user/domain skills while preserving the base model’s spectrum and capabilities; apply layerwise KL budgets to bound drift.
- Potential Products: “Safe RL personalization” services; domain‑specific adapters configured for low‑curvature subspaces.
- Assumptions/Dependencies: Reliable verifiable rewards for user tasks; scalable geometry metrics; privacy‑preserving RLHF.
- Parameter‑space safety: anomaly and backdoor detection via geometry signatures
- Sectors: security, trust/safety, policy
- What: Detect suspicious fine‑tunes by monitoring deviations from spectrum‑preserving, off‑principal patterns (e.g., large principal‑subspace rotations or concentrated principal updates).
- Potential Products: Geometry‑based anomaly detectors; compliance scanning of RLHF artifacts.
- Assumptions/Dependencies: Baseline signatures for each model; thresholds calibrated to avoid false positives; access to weight diffs.
- Precision‑adaptive training and hardware/software co‑design
- Sectors: ML systems, hardware vendors
- What: Dynamically adapt precision and learning rates to ensure micro‑updates are realized where needed without misleading sparsity; hybrid storage (bf16/fp32) for critical layers.
- Potential Products: Precision‑aware RL schedulers; mixed‑precision policies tuned by geometry metrics.
- Assumptions/Dependencies: Runtime support for per‑layer precision control; performance–cost tradeoff studies.
- Cross‑model adapter re‑orientation via learned geometry translators
- Sectors: foundation model providers, MLOps
- What: Translate adapters across model families by reorienting them into the target model’s off‑principal subspaces, preserving spectrum while transferring skills.
- Potential Products: Adapter translators; geometry alignment tools for multi‑model fleets.
- Assumptions/Dependencies: Stable geometry estimations across models; availability of function‑preserving reparameterizations; empirical validation at scale.
- Standards and benchmarks for RL post‑training geometry
- Sectors: academia, policy, industry consortia
- What: Establish open benchmarks and reporting standards for KL budgets, spectral drift, principal‑angle rotation, and update–principal overlap in RLVR, RLHF, and agent training.
- Potential Products: Shared leaderboards; standardized telemetry schemas; evaluation suites.
- Assumptions/Dependencies: Community adoption; reference implementations; data/model access for reproducibility.
- Curriculum and pedagogy integrating Three‑Gate Theory
- Sectors: academia, education
- What: Teach KL‑anchored RL dynamics, model geometry, and precision effects; develop labs that build bf16‑aware probes and spectrum‑monitoring.
- Potential Products: Course modules; open lab kits; sandboxed RLVR exercises.
- Assumptions/Dependencies: Accessible models; educational compute budgets.
Notes on feasibility across applications:
- The approach presumes a pretrained model with structured geometry; training from scratch may not exhibit the same bias.
- Verifiable rewards and KL regularization or ratio clipping are core to the observed dynamics.
- Per‑layer SVD and geometry monitoring are computationally intensive for very large models; approximations or learned proxies may be needed.
- Adapter orientation and mask‑based updates require framework support to target specific weight subsets.
- The “apparent sparsity” depends on bf16 precision; conclusions must be validated when storage or precision settings change.
Glossary
- Advantage estimate: A scalar signal used in policy gradient methods to indicate how much better or worse an action (or trajectory) is than a baseline. "a (normalized) advantage estimate"
- bfloat16 (bf16): A 16-bit floating-point format with 8-bit exponent and 7-bit mantissa, offering wide range but limited precision; widely used for training throughput. "bfloat16 (bf16) is standard in modern RL frameworks like verl"
- Bernoulli baseline: The expected overlap baseline assuming independent Bernoulli trials at a given sparsity level. "independent Bernoulli baseline"
- Consensus ratio: The fraction of runs that updated a given parameter coordinate, used to measure cross-run update locality. "consensus ratio"
- DAPO: A clip-only reinforcement learning variant (no explicit KL regularization term) used in RLVR training. "DAPO"
- DPO: Direct Preference Optimization, an RLHF-style objective optimizing from pairwise preferences rather than numeric rewards. "DPO"
- Fisher information: The curvature matrix of a statistical model that measures sensitivity of the log-likelihood to parameter changes; acts as a local metric. "let denote the Fisher information"
- Forward-KL drift: Increase in the KL divergence from reference to learned policy measured in the forward direction; used to monitor stability. "forward-KL drift"
- Function-preserving orthogonal rotations: Weight-space transformations that keep the network’s function unchanged while altering its parameter geometry. "function-preserving orthogonal rotations abolish the effect of update locality overlap"
- Gate I (KL Anchor): The first component of the Three-Gate Theory, asserting that KL constraints anchor each RL step near the current policy. "Gate I (KL Anchor)"
- Gate II (Model Geometry): The second component of the Three-Gate Theory, positing that pretrained geometry steers KL-bounded updates into low-curvature, off-principal subspaces. "Gate II (Model Geometry)"
- Gate III (Precision): The third component of the Three-Gate Theory, noting finite-precision storage hides micro-updates and makes the bias appear as sparsity. "Gate III (Precision)"
- GRPO: Group Relative Policy Optimization, an RL objective variant used for verifiable-reward training. "GRPO"
- Jaccard Overlap: A set-similarity metric defined as intersection over union, used here to compare update masks across runs. "using Jaccard Overlap."
- KL divergence: The Kullback–Leibler divergence; a measure of dissimilarity between probability distributions, used as a proximity regularizer. "bounded KL divergence change"
- KL leash: An implicit per-step constraint that keeps the updated policy close to the current one under KL metrics. "Oneâstep policyâKL leash"
- Ky Fan k-norm: The sum of the top k singular values of a matrix, capturing top-k spectral energy. "Ky Fan -norm"
- Large Reasoning Models (LRMs): LLMs with enhanced multi-step reasoning capabilities. "Large Reasoning Models (LRMs)"
- LoRA: Low-Rank Adaptation; a parameter-efficient method that injects trainable low-rank matrices into weight updates. "LoRA"
- Mixture-of-Experts: An architecture that routes inputs through a subset of expert sub-networks, increasing capacity without proportional compute. "Mixture-of-Experts"
- M-projection: The information-geometry projection that minimizes KL divergence from a target distribution to a parametric family. "the âprojection of onto the policy class"
- Model-conditioned optimization bias: A stable preference of updates to land in specific parameter regions determined by the pretrained model’s geometry. "model-conditioned optimization bias"
- Normalized spectral drift: The relative L2 change of the singular value spectrum between base and fine-tuned weights. "normalized spectral drift."
- Off-principal directions: Directions in weight space orthogonal to top singular subspaces; associated here with low curvature and RLVR updates. "off-principal directions"
- On-policy: Using samples generated by the current policy to perform updates, as opposed to off-policy data. "on-policy step"
- Parameter-efficient fine-tuning (PEFT): Techniques that adapt a model with few additional or updated parameters (e.g., LoRA) rather than full-model updates. "parameter-efficient fine-tuning (PEFT)"
- PiSSA: A LoRA-like variant that targets principal components/weights, typically aligned with SFT geometry. "PiSSA"
- Policy gradient: A class of RL algorithms that optimize expected reward by ascending the gradient of the policy’s parameters. "policy gradient methods"
- PPO: Proximal Policy Optimization; a KL-regularized policy-gradient algorithm with ratio clipping. "PPO"
- Principal angles: Canonical angles between subspaces used to quantify rotation between singular subspaces before and after fine-tuning. "principal angles"
- Principal mask: A binary mask selecting weights aligned with top-k singular subspaces (via rank-k SVD reconstruction). "principal mask"
- Principal-subspace rotation: The change in orientation of top-k singular subspaces of a weight matrix after training. "principal-subspace rotation"
- Principal weights: Weights associated with the top singular directions (from rank-k SVD reconstruction) that carry high spectral energy. "principal weights"
- Rank-k SVD reconstruction: The approximation of a matrix using only its top k singular values/vectors. "rank- SVD reconstruction"
- Ratio clipping: The PPO-style technique that clips importance ratios to limit update magnitude and stabilize training. "ratio clipping trick"
- REINFORCE++: A reinforcement learning variant related to REINFORCE, used here as an RLVR algorithm. "REINFORCE++"
- Reinforcement Learning with Verifiable Rewards (RLVR): RL post-training that uses automatically checkable rewards (e.g., pass/fail) to drive reasoning improvements. "Reinforcement Learning with Verifiable Rewards (RLVR)"
- RLHF: Reinforcement Learning with Human Feedback, where rewards or preferences come from humans rather than programmatic verifiers. "RL with human feedback (RLHF)"
- Singular subspaces: The subspaces spanned by left/right singular vectors associated with singular values of a matrix. "top- singular subspaces"
- Spectrum-preserving subspaces: Directions of change that minimally affect the singular value spectrum of the weights. "spectrum-preserving subspaces"
- Three-Gate Theory: The proposed mechanism (KL Anchor, Model Geometry, Precision) explaining RLVR’s update patterns. "Three-Gate Theory"
- Unit-in-the-last-place (ULP): The spacing between adjacent floating-point numbers at a given magnitude; sets the smallest representable change. "unit-in-the-last-place (ULP) threshold"
- Update sparsity: The fraction of weights that appear unchanged after training (often inflated by finite precision). "Update sparsity in SFT vs.\ RLVR."
- Wedin’s sin–Θ theorem: A perturbation bound relating spectral gaps and operator-norm perturbations to subspace rotation. "Wedinâs sin-- theorem"
Collections
Sign up for free to add this paper to one or more collections.