Defeating the Training-Inference Mismatch via FP16 (2510.26788v1)
Abstract: Reinforcement learning (RL) fine-tuning of LLMs often suffers from instability due to the numerical mismatch between the training and inference policies. While prior work has attempted to mitigate this issue through algorithmic corrections or engineering alignments, we show that its root cause lies in the floating point precision itself. The widely adopted BF16, despite its large dynamic range, introduces large rounding errors that breaks the consistency between training and inference. In this work, we demonstrate that simply reverting to \textbf{FP16} effectively eliminates this mismatch. The change is simple, fully supported by modern frameworks with only a few lines of code change, and requires no modification to the model architecture or learning algorithm. Our results suggest that using FP16 uniformly yields more stable optimization, faster convergence, and stronger performance across diverse tasks, algorithms and frameworks. We hope these findings motivate a broader reconsideration of precision trade-offs in RL fine-tuning.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper looks at why training LLMs with reinforcement learning (RL) can be unstable and sometimes “collapse” (stop improving or get worse). The authors find a surprisingly simple fix: use FP16 (a 16-bit number format with higher precision) instead of BF16 (another 16-bit format that’s popular today). This change reduces small numerical errors that make the model behave differently during training versus during inference, and it makes training more stable, faster, and better across many models and methods.
Key Questions
The paper asks three main questions, in simple terms:
- Why do models act differently when they’re trained vs. when they’re used (inference), even though they’re supposed to be the same?
- Is the root cause of this difference the number format used in the computer (BF16 vs. FP16)?
- If we switch to FP16 everywhere, do we get more stable training and better results without complicated algorithm fixes?
Methods and Approach
Think of training and inference like using two calculators that should give the same answer. In reality, they use slightly different shortcuts and number formats, so they round numbers differently. Tiny rounding differences can snowball as the model generates many tokens (words), making the “training calculator” and the “inference calculator” disagree more and more. That’s the “training–inference mismatch.”
Here’s what the authors did:
- Precision comparison: They compare BF16 and FP16. Both are 16-bit formats, but they split those bits differently:
- BF16 has more “range” (it can represent very big and very small numbers) but less “precision” (fewer fine-grained steps between numbers).
- FP16 has slightly less range but more precision (smaller steps between numbers), so rounding is much gentler.
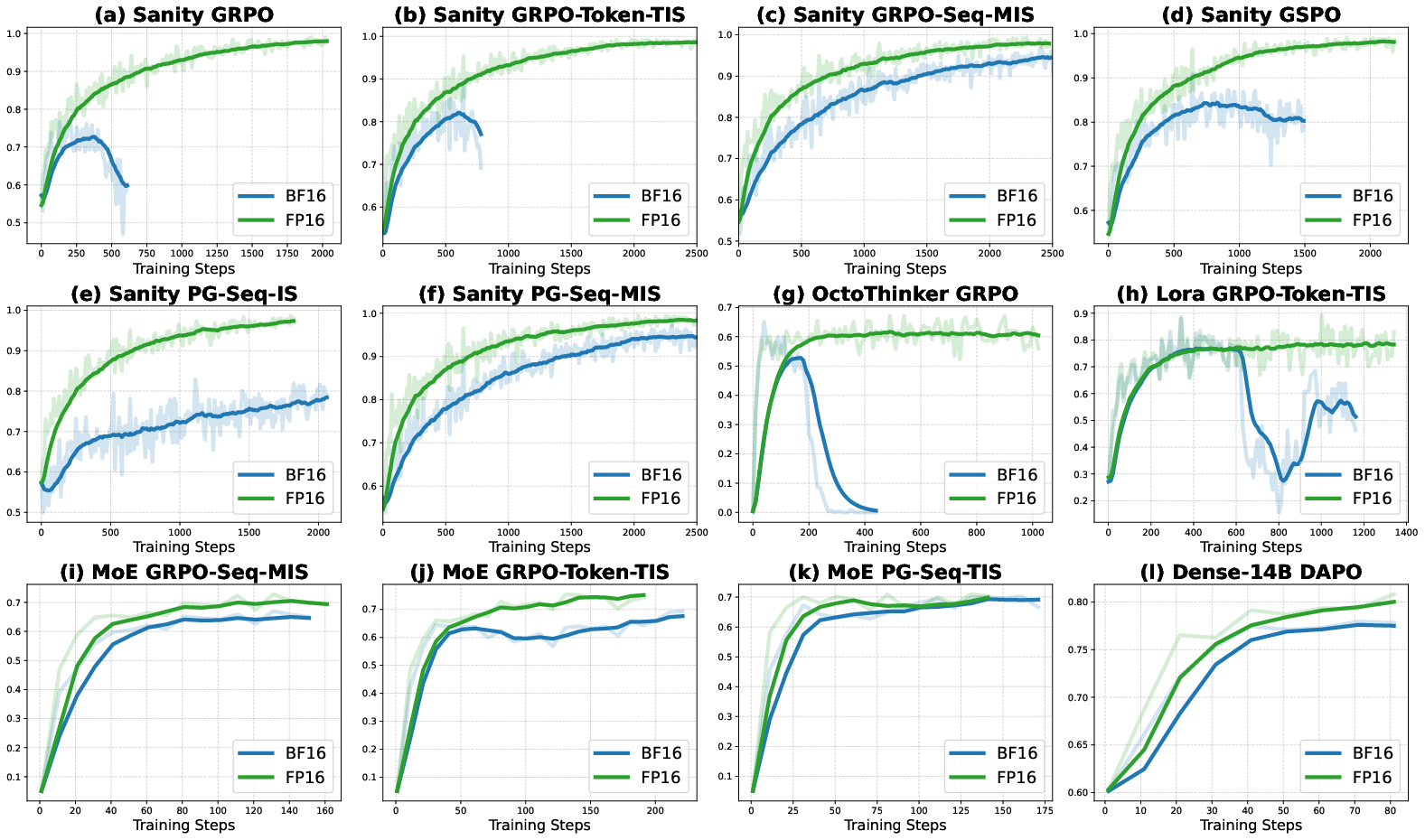
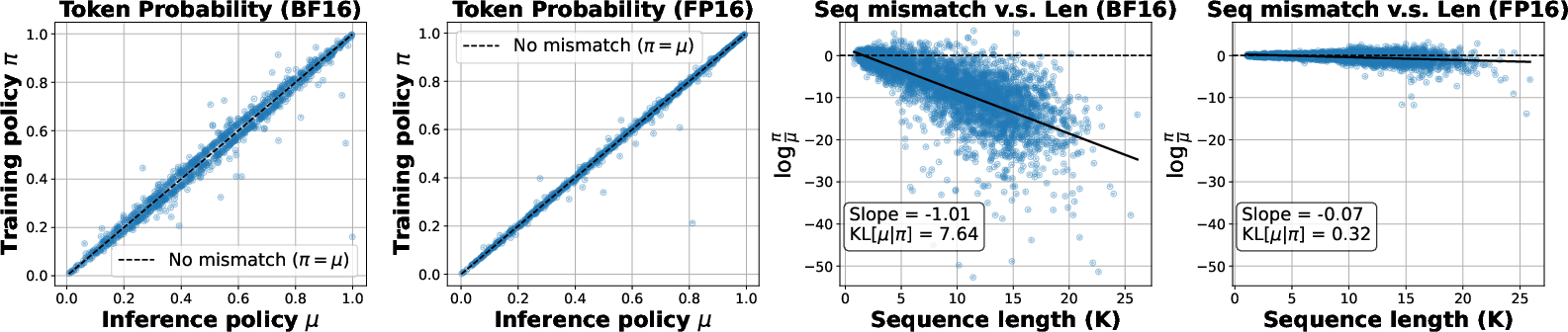
- Offline checks: They measured how much the training and inference steps disagree when using BF16 vs. FP16, both at the token level (each step of generation) and the full sequence level (the entire response). FP16 showed far less mismatch.
- A “sanity test” dataset: They built a special set of math problems that are not trivial but are solvable by the base model. On this set, a reliable RL method should reach near 100% training accuracy. This makes it clear whether training methods are truly stable and effective.
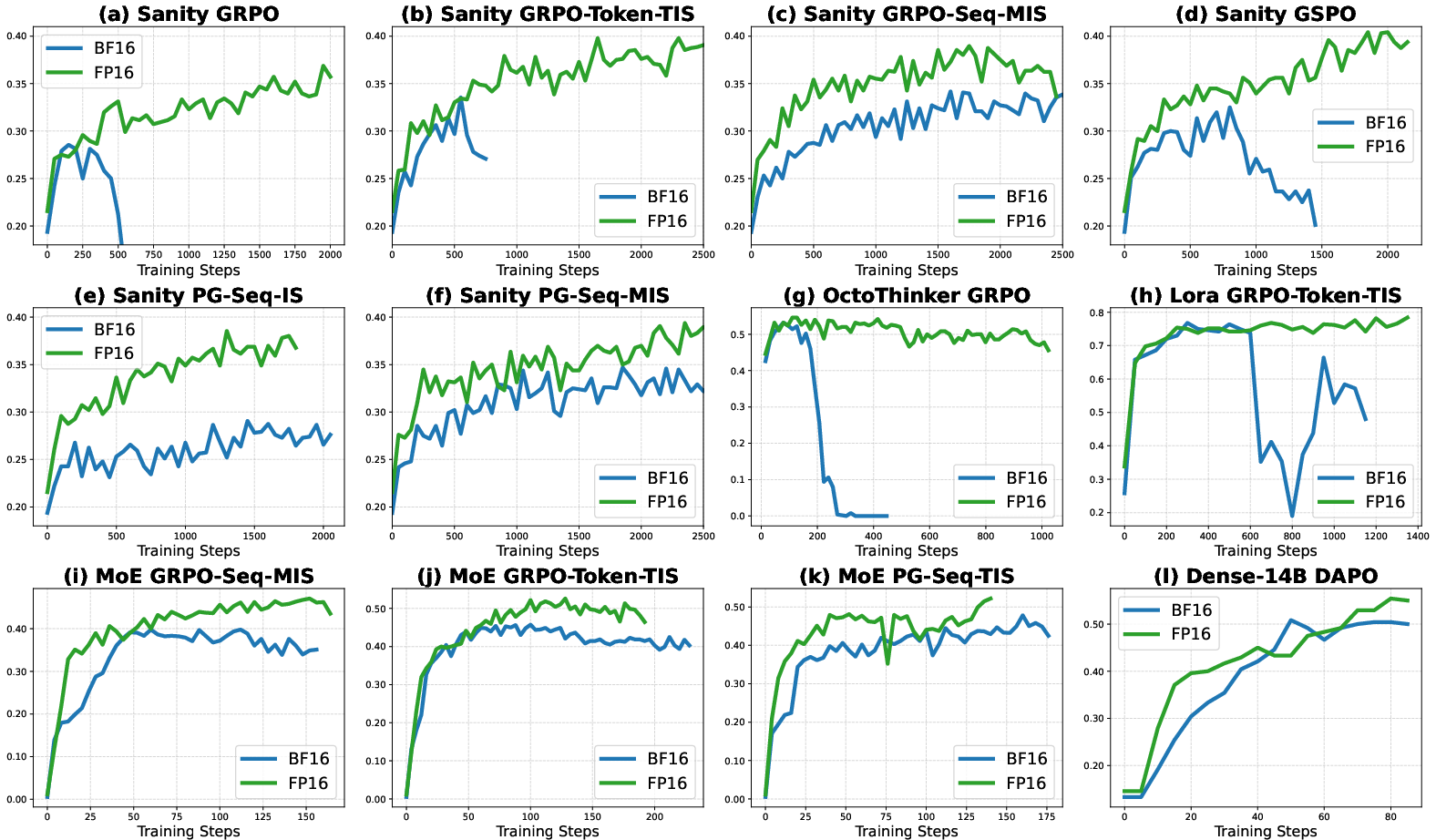
- Many experiments: They tested across different algorithms (like GRPO and importance sampling methods), different frameworks (VeRL and Oat), different model families (Qwen, OctoThinker), different training styles (full fine-tuning and LoRA), and larger models (dense and mixture-of-experts). They also tried different combinations: BF16 training with FP16 or FP32 inference versus FP16 training + inference.
Technical terms explained with simple analogies:
- Floating point precision: Like using a ruler with markings. BF16’s ruler has fewer markings (coarser steps), FP16’s has more markings (finer steps), so measurements are more precise and less round-off happens.
- Importance sampling: Imagine collecting votes from a crowd where some votes are over- or under-represented. Importance sampling reweights the votes so you get a fair result. In RL, it corrects for differences between how you sampled the model’s output and how you train it.
- Loss scaling (for FP16): If some gradients are too tiny to represent with FP16, the system temporarily multiplies everything by a big number so the tiny values don’t become zero, then divides back later. Most modern tools do this automatically.
Main Findings
- FP16 greatly reduces the mismatch: With FP16, the probabilities computed during training and inference line up much more closely. That means the model gets consistent signals and doesn’t “drift” or collapse.
- Better stability and speed: Training with FP16 converges faster and stays stable for longer (often all the way through), compared to BF16, which frequently collapses or needs complicated fixes.
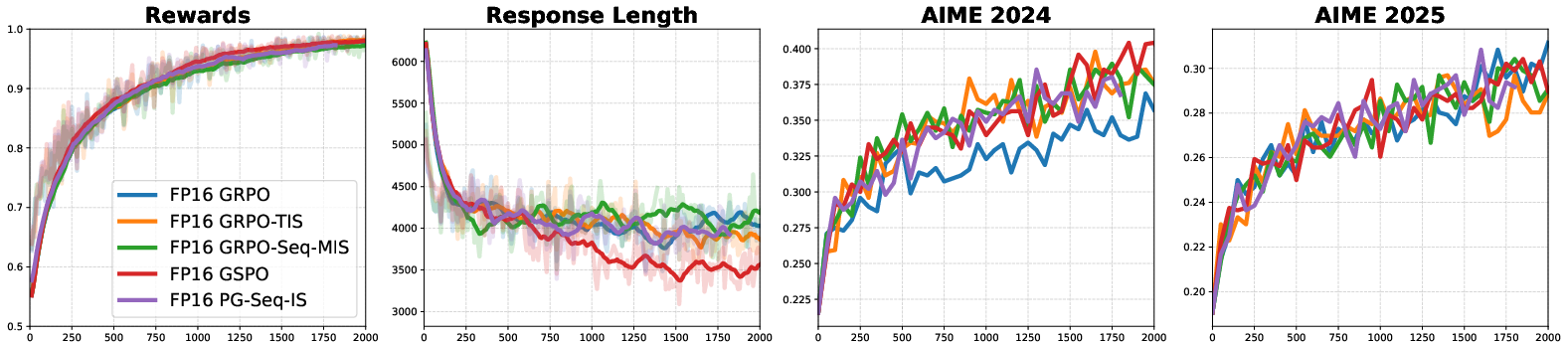
- Simpler algorithms work better: Using FP16, the classic, simple policy gradient with importance sampling works very well and outperforms BF16 methods that add complex patches. FP16 lowers both the bias (error from mismatch) and the variance (wild swings from corrections), so training becomes smooth and efficient.
- Less “deployment gap”: Models trained under FP16 behave similarly when later used for inference, so performance in the real world matches what you saw during training more closely.
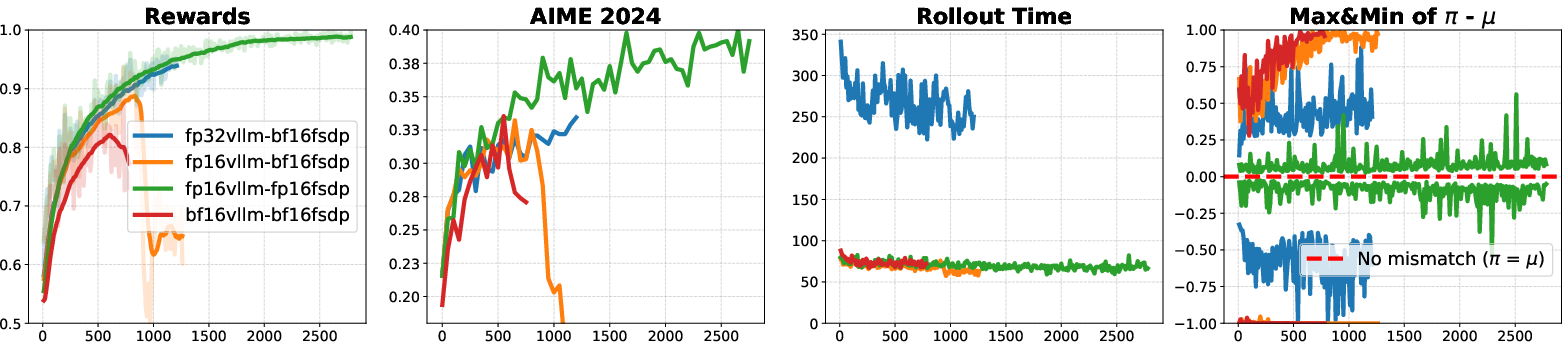
- Broad generalization: These benefits show up across many models (dense and mixture-of-experts), training styles (full fine-tuning and LoRA), and RL algorithms, and in different code frameworks. Even when BF16 training is paired with very precise FP32 inference, you can get stability—but it’s much slower. FP16 training + inference is the sweet spot: stable and fast.
Implications and Impact
This paper suggests a simple, practical change for RL fine-tuning of LLMs: use FP16 everywhere. While BF16 is great for big pre-training because it avoids overflow/underflow, its lower precision causes rounding differences that hurt RL fine-tuning, where training and inference must agree closely. Switching to FP16:
- Reduces the need for complicated algorithm patches and extra computation.
- Makes training more reliable and faster.
- Improves final performance and narrows the gap between training-time and deployment-time behavior.
In short, choosing FP16 for RL fine-tuning helps keep the “two calculators” consistent. That small change can make a big difference, turning unstable training into stable, strong results across many models and methods.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, focused list of what remains missing, uncertain, or unexplored in the paper, formulated to be actionable for future research.
- Lack of a formal numerical analysis: no theoretical bounds or models quantifying how BF16 rounding error accumulates token-by-token to induce policy divergence versus FP16 (e.g., closed-form error propagation through softmax/log-prob computations over sequence length).
- Missing operator-level attribution: the paper does not identify which specific operations (e.g., softmax, logit normalization, layer norm, attention score scaling, MoE routing/top-k, sampling kernels) contribute most to the training–inference mismatch under BF16.
- Unclear failure modes of FP16: no systematic paper of when FP16’s limited dynamic range (overflow/underflow) causes instability during RL fine-tuning, nor concrete guidelines for safe ranges, gradient scales, or mitigation strategies beyond stating “use loss scaling.”
- Loss scaling specifics are underexplored: the paper does not ablate static vs. dynamic loss scaling, scaling schedules, overflow detection thresholds, or synchronization strategies in distributed settings (ZeRO/FSDP) and their impact on stability, throughput, and variance.
- Incomplete hardware generalization: results are on NVIDIA A100 GPUs; behavior on H100/L40/consumer GPUs, TPUs, and different CUDA/cuDNN/TransformerEngine versions is unknown, including the impact of hardware-level BF16/FP16 rounding and fused kernel implementations.
- Limited framework coverage: only VeRL and Oat are tested; it’s unclear whether results hold across other RL stacks and inference engines (e.g., TRLX, TorchRL, JAX/TPU stacks, HuggingFace Accelerate, vLLM variants, TensorRT-LLM).
- Scale limits not characterized: no evidence for extremely large dense/MoE models (e.g., >70B parameters or large expert counts), where FP16’s smaller exponent range may be problematic; practical upper bounds and safeguards remain unspecified.
- Task diversity is narrow: experiments focus on math reasoning; the effect of FP16 vs BF16 on coding, multi-turn dialogue, RLHF with human preference models, safety alignment tasks, and open-ended generation remains untested.
- Decoding policy effects are underexplored: mismatch was analyzed at temperature 1.0 without top-p; typical RL uses nucleus/top-k sampling and temperature schedules—how decoding hyperparameters modulate mismatch and IS variance is not studied.
- Importance sampling variance quantification is limited: while FP16 reduces mismatch, the paper lacks quantitative IS variance benchmarks across sequence lengths, tasks, and algorithms, and does not provide principled clipping/threshold guidelines (e.g., how to choose C).
- Statistical robustness is unclear: few or no multi-seed runs, confidence intervals, or significance tests; sensitivity to random seeds and stochastic system nondeterminism is not characterized.
- Deployment gap measurement is not definitive: the paper claims FP16 “closes” the gap but does not directly quantify post-training divergence between training and inference engines or specify acceptance criteria for “closed” (e.g., tolerable log-prob ratio thresholds).
- Efficiency trade-offs lack hard numbers: no end-to-end throughput/memory benchmarks comparing BF16 vs FP16 for both training and inference, including the overhead of dynamic loss scaling and any communication or kernel-level performance differences.
- Minimal-change precision strategies untested: the paper does not explore whether switching only critical numerics (e.g., logits/softmax/routing) to FP16 while keeping the rest in BF16 is sufficient to eliminate mismatch with lower engineering risk.
- Hyperparameter interactions are not mapped: how FP16 influences optimal learning rates, gradient clipping norms, entropy regularization, PPO/GRPO clip settings, batch sizes, and credit assignment choices is not systematically examined.
- Behavioral impacts of precision are unknown: potential changes in exploration entropy, response diversity, calibration, and reward hacking tendencies under FP16 vs BF16 are not evaluated.
- FP8 and lower-precision pathways are speculative: the paper suggests FP8 may be viable but provides no empirical or theoretical assessment of training–inference mismatch and stability under FP8 (or mixed FP8/FP16) in RL fine-tuning.
- Distributed training details are thin: concrete recipes for stable FP16 across ZeRO/FSDP (e.g., gradient scaling synchronization, overflow handling, mixed-precision optimizer states) are not provided or validated across backends.
- Sequence-length sensitivity lacks thresholds: while mismatch grows with length under BF16, actionable guidance (e.g., max safe generation lengths for BF16, length-dependent IS clipping) is missing.
- MoE routing sensitivity under FP16 is unknown: potential effects of FP16 precision on gate logits/top-k selection stability (e.g., tie-breaking, expert load imbalance, routing jitter) are not measured.
- Inference engine variability is not isolated: differences across vLLM/HF Transformers/custom inference stacks and their numerical kernels are not systematically compared for mismatch under BF16 vs FP16.
- LoRA-specific precision tuning is unexplored: how FP16 affects optimal LoRA rank/alpha, adapter placement, and stability compared to BF16 (and whether mixed-precision adapters suffice) is not ablated.
- Precision combination space is incomplete: beyond a limited ablation, the paper does not map the broader design space (e.g., FP16 training with BF16 inference; BF16 training with selective FP16 inference components) to find cost-effective stable combinations.
- Transition effects from BF16-pretrained bases are not studied: whether switching a BF16-pretrained model to FP16 during RL requires rescaling/calibration and how that impacts numerics and stability is unknown.
- Real-world deployment constraints are unaddressed: many production stacks favor BF16 or INT8; practical migration paths, compatibility risks, and interactions with post-training quantization (INT8/INT4) are not discussed.
- Reward model precision effects are untested: in RLHF settings, the precision of the reward model (BF16 vs FP16) and its interplay with the policy’s precision during training/inference are not examined.
- Sanity test generalization risk: achieving near-100% training accuracy on the filtered “perfectible” dataset may overfit; the extent to which improvements transfer to the full, unfiltered distribution is not measured.
- Reproducibility artifacts: exact code configurations (e.g., precision flags, kernel settings, optimizer dtypes, seed/nondeterminism controls) needed to reproduce FP16 stability are not fully enumerated for cross-environment validation.
Practical Applications
Immediate Applications
The paper’s findings enable concrete, low-effort changes to existing RL fine-tuning pipelines that improve stability, convergence speed, and deployment performance. The following applications can be adopted now, provided standard FP16 support and dynamic loss scaling are available in your stack.
- Switch RL fine-tuning precision from BF16 to FP16 across training and inference
- Sector: software/AI platforms; LLM productization
- Workflow: configure training to use FP16 with dynamic loss scaling and set inference engines (e.g., vLLM, Triton, custom CUDA kernels) to FP16
- PyTorch: enable
torch.cuda.amp.GradScaler()andautocast(dtype=torch.float16) - DeepSpeed/FSDP/Megatron: set
fp16: true,bf16: false; enable dynamic loss scaling - vLLM or serving layer: set model weights and kernels to FP16 on deployment
- Benefits: lower training–inference mismatch, fewer collapses, faster convergence, higher eval scores, closed deployment gap
- Assumptions/dependencies: hardware supports FP16; gradients/activations stay within range when loss scaling is used; training and inference both use FP16 consistently
- Simplify RL algorithms by removing mismatch patches (e.g., token-level TIS, sequence-level MIS) and using unbiased policy gradient with importance sampling
- Sector: software/AI development; research
- Tools: implement standard PG-Seq-IS; avoid extra forward pass used by GRPO-based off-policy corrections
- Benefits: ~25% training cost reduction; lower variance under FP16; less algorithmic complexity
- Assumptions/dependencies: FP16 adopted end-to-end; policy mismatch monitoring shows stable IS ratios
- Add mismatch monitoring as an early-warning signal in RL training dashboards
- Sector: MLOps/observability
- Tools/products: real-time metrics for token-level and sequence-level log-prob ratios between rollout and trainer engines; alerts on spikes
- Benefits: proactive collapse detection; automatic mitigations (reduce LR, reset scaler, switch precision)
- Assumptions/dependencies: access to both engines’ log-probs; lightweight logging overhead
- Adopt the “perfectible dataset” sanity test for evaluating RL algorithms and system changes
- Sector: academia/industry R&D
- Workflow: filter tasks with 20–80% initial accuracy to form solvable-but-nontrivial sets; set >95% training accuracy as pass threshold
- Benefits: disambiguates algorithm failures from model limits; faster diagnostics and A/B testing
- Assumptions/dependencies: ability to generate multiple rollouts per item; reward function correctness
- Stabilize MoE and LoRA-based RL pipelines by defaulting to FP16
- Sector: software/LLM labs; model architecture teams
- Workflow: use FP16 with dynamic loss scaling for MoE gating/top-k policies; apply FP16 to LoRA adapters and base layers
- Benefits: higher training accuracy, fewer NaNs/spikes, reduced mismatch in expert selection and adapter paths
- Assumptions/dependencies: careful management of top-k operations; loss scaling synchronized across workers; MoE kernels well-tested in FP16
- Reduce deployment gap and improve evaluation fidelity
- Sector: production LLMs; customer-facing apps
- Workflow: ensure inference precision matches training precision (FP16) in serving infrastructure
- Benefits: trained parameters optimized for the same engine used in deployment; fewer post-training regressions
- Assumptions/dependencies: serving stack can run FP16 without forced precision conversions
- Establish internal precision guidelines for RL fine-tuning
- Sector: organizational policy/engineering standards
- Policy/document: “Use FP16 + dynamic loss scaling for RL fine-tuning; monitor mismatch; only use BF16 if FP16 instability persists and mismatch is acceptable”
- Benefits: improved reproducibility; fewer emergency retrains; standardized practice
- Assumptions/dependencies: governance supports experimentation to validate the change
- Educational modules on precision trade-offs in RL
- Sector: education/training programs
- Tools: hands-on labs demonstrating BF16 vs FP16 mismatch effects; exercises with importance sampling ratios under different dtypes
- Benefits: better practitioner intuition about numerics; fewer brittle engineering fixes
- Assumptions/dependencies: access to GPUs and small RL tasks; reproducible setups
- Lightweight tooling to enforce precision consistency
- Sector: tooling/ecosystem
- Product ideas: config linters that flag mixed BF16/FP16 in training/inference; adapters that normalize dtype across frameworks (VeRL, Oat, FSDP)
- Benefits: prevents silent mismatch; reduces debugging time
- Assumptions/dependencies: hooks into training/inference config files; minimal runtime overhead
Long-Term Applications
These opportunities require further engineering, research, or ecosystem changes to reach scale or generalize beyond LLM RL.
- Numerics-aligned, unified training–inference engines
- Sector: software infrastructure; compilers
- Product: single-kernel stacks that guarantee identical rounding paths for rollout and trainer modes; verified equivalence at the op level
- Benefits: eliminates mismatch by construction; lowers reliance on precision choices
- Dependencies: significant kernel engineering; cross-framework standardization; performance parity
- Precision-aware orchestration systems that auto-switch dtypes
- Sector: MLOps/platforms
- Product: controllers that monitor mismatch metrics and dynamically switch between FP16, BF16, FP32, or FP8 based on stability and cost
- Benefits: optimal trade-off between speed, stability, and accuracy across training phases
- Dependencies: robust metric pipelines; deterministic fallback strategies; cost models per dtype
- Hardware and format innovation tailored to RL fine-tuning
- Sector: hardware/accelerators
- Direction: low-precision formats with higher mantissa (e.g., FP8 variants emphasizing precision) and hardware loss scaling; numerics co-design for MoE gating
- Benefits: FP16-like precision at FP8 costs; stability in massive models
- Dependencies: vendor support; compiler/runtime maturity; workload validation
- Precision-aware RL algorithms that exploit lower mismatch
- Sector: academia/algorithm research
- Direction: IS estimators with adaptive clipping based on observed ratios; hybrid on/off-policy methods tuned for FP16 numerics; length-aware variance control
- Benefits: faster convergence with theoretical guarantees; scalable to long sequences
- Dependencies: rigorous variance analysis; benchmarks beyond math reasoning
- Standardization of reproducibility and stability checks
- Sector: policy/standards; conferences and consortia
- Proposal: guidelines requiring reporting of training–inference mismatch metrics, precision settings, and sanity-test pass rates for RL papers/products
- Benefits: more trustworthy results; easier cross-paper comparisons
- Dependencies: community adoption; tooling support; reviewer education
- Safety/alignment monitoring based on mismatch indicators
- Sector: AI safety; governance
- Product: monitors that treat escalating mismatch as a proxy for unstable optimization or emergent failure modes; automatic intervention policies
- Benefits: lower risk of collapse-induced behaviors; safer RLHF/RLAIF training
- Dependencies: correlation studies between mismatch and harmful outputs; policy integration
- Precision-aware distributed protocols for extreme-scale FP16 training
- Sector: distributed systems
- Direction: efficient synchronization of dynamic loss scaling across thousands of workers; overflow/underflow detection with low latency
- Benefits: unlocks FP16 stability at 100B+ parameter scale
- Dependencies: new collective ops; fault tolerance strategies; compatibility with ZeRO/FSDP
- Extending precision-aware RL to other domains (robotics, energy, finance)
- Sector: robotics/control; energy optimization; quantitative finance
- Use case: mitigate rollout–trainer discrepancies in simulators vs on-device control by adopting FP16 or precision-aligned engines; improve policy transfer
- Benefits: more reliable deployment in non-LLM RL settings
- Dependencies: domain-specific kernels; validation in real-world environments; safety certification
Notes on assumptions and dependencies (cross-cutting)
- FP16 adoption presumes dynamic loss scaling is correctly implemented and synchronized in distributed training; without it, gradient underflow/overflow may occur.
- Some frameworks have bespoke inference/training kernels; FP16 reduces but may not fully eliminate mismatch if kernels diverge semantically.
- Very large models or unusual activations may still stress FP16 range; monitoring and fallback to BF16/FP32 for specific layers may be necessary.
- Reported benefits were measured on math reasoning tasks and common RL algorithms (GRPO, GSPO, PG); generalization to all tasks should be validated.
Glossary
- Ablation study: A controlled experiment to isolate the effect of a specific factor by varying it while holding others constant. "we conducted an ablation study on the VeRL framework, using vLLM for inference and PyTorch FSDP for training."
- Advantage: In policy gradient RL, the baseline-adjusted reward signal that reduces variance in gradient estimates. "The term is the advantage, with serving as a baseline for variance reduction"
- Auto-regressive generation: Sequential token generation where each token is conditioned on previously generated tokens. "tokens are generated auto-regressively during inference"
- Baseline (variance reduction): A reference value subtracted from rewards to reduce variance in policy gradient estimates. "with serving as a baseline for variance reduction"
- BF16 (BFloat16): A 16-bit floating-point format with 8 exponent bits and 7 mantissa bits; wide dynamic range but lower precision. "The widely adopted BF16, despite its large dynamic range, introduces large rounding errors"
- Biased gradient: A gradient estimator whose expectation does not equal the true gradient due to sampling or mismatch issues. "While algorithmic patches~\citep{yao2025offpolicy, liu-li-2025} fix the biased gradient"
- Clipping hyperparameter: A threshold used to cap magnitude (e.g., of importance weights) for stability. "where is a clipping hyperparameter and is the indicator function."
- DAPO: A specific RL optimization algorithm used for LLM fine-tuning. "we experiment with Qwen3-14B-Base and follow the algorithm of DAPO"
- DeepSpeed ZeRO: A memory- and compute-optimization approach for distributed training that shards optimizer states, gradients, and parameters. "their different distributed backends (DeepSpeed ZeRO vs. PyTorch FSDP)"
- Deployment gap: The performance discrepancy arising when models are trained with one engine/policy and deployed with another. "Another important but hard to fix issue is the deployment gap."
- Dr.GRPO: A GRPO variant designed to remove length and difficulty biases in the training objective. "We use the Dr.GRPO variant to remove the length and difficulty biases of the vanilla GRPO."
- Dynamic loss scaling: Automatic adjustment of the loss scaling factor during mixed-precision training to avoid overflow/underflow. "Modern implementations have further improved this with dynamic loss scaling."
- Dynamic range: The span of representable numeric values in a floating-point format. "The widely adopted BF16, despite its large dynamic range, introduces large rounding errors"
- Exponent bits: The portion of a floating-point format’s bit budget that encodes the numeric range. "Exponent Bits"
- FP16: IEEE 754 half-precision (5 exponent bits, 10 mantissa bits) offering higher precision than BF16 but smaller range. "by switching from BF16 to the FP16 during RL fine-tuning, we can virtually eliminate the training-inference mismatch."
- FP32: IEEE 754 single-precision (8 exponent bits, 23 mantissa bits), often used as a high-precision baseline. "matching the range of the 32-bit FP32 format"
- FSDP (PyTorch FSDP): Fully Sharded Data Parallel; shards model states across devices to scale training efficiently. "PyTorch FSDP"
- GRPO: A GRPO-based policy gradient method commonly used in LLM RL, often with clipping and group baselines. "The standard GRPO gradient"
- GSPO: An RL algorithm related to group-wise optimization; used as a baseline in mismatch studies. "We include GSPO~\citep{zheng2025group} in our experiments"
- Importance sampling (IS): A technique that reweights samples from one distribution to estimate expectations under another. "a principled approach is to use importance sampling (IS)."
- Indicator function: A function that equals 1 if a condition holds and 0 otherwise, used to mask updates. "and is the indicator function."
- LoRA (Low-Rank Adaptation): A parameter-efficient fine-tuning method that injects low-rank adapters into pretrained weights. "LoRA~\citep{hu2022lora} has recently regained popularity in LLM RL"
- Loss scaling: Multiplying the loss before backpropagation to prevent gradient underflow in low-precision training. "with a technique called loss scaling"
- Mantissa bits: The portion of a floating-point format that encodes precision within the representable range. "With more mantissa bits, FP16 offers higher numerical precision"
- Masked Importance Sampling (MIS): An IS variant that masks (drops) updates with extreme importance ratios to reduce variance. "Masked Importance Sampling (MIS)"
- Mixture-of-Experts (MoE): A model architecture that routes tokens to a subset of specialized expert networks. "Mixture-of-Experts (MoE) models"
- Off-policy: Using data generated by a behavior policy different from the current training policy. "which may differ from in an off-policy setting."
- Overflow: Numeric values exceeding the representable maximum in a floating-point format. "overflow (values exceeding the representable maximum)"
- Policy gradient: A family of RL methods that directly optimize the policy by ascending the expected return gradient. "The policy gradient can be calculated by REINFORCE estimator"
- Policy iteration: An optimization scheme alternating between data collection (policy evaluation) and policy improvement steps. "For each policy iteration~\citep{schulman2017proximal}, we use a batch size of 64 questions"
- REINFORCE estimator: The classic Monte Carlo policy gradient estimator using log-probability gradients times returns/advantages. "The policy gradient can be calculated by REINFORCE estimator"
- RLOO: Reinforcement Learning with Leave-One-Out baselines for variance reduction. "and RLOO~\citep{ahmadian2024back, kool2019buy}"
- Rollout: The process/engine used to generate trajectories (token sequences) under a policy for training or evaluation. "a highly optimized one for fast inference (rollout)"
- Sequence-level importance sampling ratio: The IS weight computed over an entire generated sequence to correct off-policy sampling. "they proposed using an unbiased, sequence-level importance sampling ratio for the correction."
- Sequence-level log-probability ratio: The log of the ratio between sequence probabilities under two policies, used to assess mismatch. "depict the distribution of sequence-level log-probability ratios across different generation lengths."
- Top-k expert selection: In MoE models, selecting the k highest-scoring experts for routing each token. "precision-sensitive operations such as top-k expert selection in Mixture-of-Experts (MoE) models"
- Truncated Importance Sampling (TIS): An IS variant that clips importance weights at a threshold C to reduce variance. "Truncated Importance Sampling (TIS)"
- Training-inference mismatch: Numerical discrepancies between training and inference engines that lead to divergent policies and instability. "A critical source of this instability stems from a fundamental discrepancy in modern RL frameworks: the training-inference mismatch."
- Underflow: Numeric values so small they round to zero in a floating-point format. "underflow (values rounding to zero)."
- vLLM: A high-throughput inference engine for LLMs used in evaluation/rollouts. "using vLLM~\citep{kwon2023efficient} for inference"
Collections
Sign up for free to add this paper to one or more collections.