Beyond the Ideal: Analyzing the Inexact Muon Update (2510.19933v1)
Abstract: The Muon optimizer has rapidly emerged as a powerful, geometry-aware alternative to AdamW, demonstrating strong performance in large-scale training of neural networks. However, a critical theory-practice disconnect exists: Muon's efficiency relies on fast, approximate orthogonalization, yet all prior theoretical work analyzes an idealized, computationally intractable version assuming exact SVD-based updates. This work moves beyond the ideal by providing the first analysis of the inexact orthogonalized update at Muon's core. We develop our analysis within the general framework of Linear Minimization Oracle (LMO)-based optimization, introducing a realistic additive error model to capture the inexactness of practical approximation schemes. Our analysis yields explicit bounds that quantify performance degradation as a function of the LMO inexactness/error. We reveal a fundamental coupling between this inexactness and the optimal step size and momentum: lower oracle precision requires a smaller step size but larger momentum parameter. These findings elevate the approximation procedure (e.g., the number of Newton-Schulz steps) from an implementation detail to a critical parameter that must be co-tuned with the learning schedule. NanoGPT experiments directly confirm the predicted coupling, with optimal learning rates clearly shifting as approximation precision changes.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper studies a modern way to train deep neural networks called the Muon optimizer. Muon often trains big models faster than the popular AdamW, but there’s a catch: Muon’s best trick depends on a fast, rough calculation instead of a slow, perfect one. Past theory only looked at the perfect version (which people don’t actually run), so this paper analyzes the real, imperfect version and explains how its “roughness” affects training speed and settings like learning rate and momentum.
Key Objectives
Here are the main questions the paper tries to answer:
- What happens to Muon’s performance when it uses an approximate shortcut instead of a perfect calculation?
- How should we change the learning rate and momentum when the shortcut is less precise?
- Can we still prove that training will steadily improve, and how much slower does it get with a rougher shortcut?
- Do real experiments match the theory’s predictions?
Methods and Approach
The authors connect Muon to a general optimization idea called a Linear Minimization Oracle (LMO), which you can think of as a helper that picks a direction to move that’s “best” under certain rules.
A simple analogy
- Imagine hiking down a mountain to reach the lowest point (training to reduce loss).
- At each step, you want to walk in the steepest downhill direction.
- The “perfect compass” tells you exactly where the steepest descent is, but it’s heavy and slow (like doing an exact SVD).
- The “quick compass” is light and fast but a bit off (like Newton–Schulz or PolarExpress): it gives you an almost-steepest direction very quickly.
Muon uses the quick compass. The paper models its inaccuracy with a number called “error” (think of it as how off your compass is). The authors then prove how this error affects training.
What is orthogonalization?
- Neural network weights are matrices. Muon tries to turn the update direction into a “nice rotation-like” step (orthogonalization) that respects the geometry of the matrix. This tends to produce stable, well-scaled moves.
- Doing this perfectly with SVD is super expensive. Fast methods like Newton–Schulz or PolarExpress approximate it using only matrix multiplications.
The setup
- Deterministic case: assumes perfect gradients (no noise) and studies how the inexact direction changes progress.
- Stochastic case: more realistic, with noisy gradients (like mini-batches) and momentum added. Here the paper shows how error affects both the update and the momentum’s behavior.
- The authors prove mathematical bounds: how quickly the gradient gets smaller, how error slows things down, and how to pick learning rate and momentum to compensate.
Main Findings
Here are the key results and why they matter:
- Less precise shortcut → slower training. If the approximation is rougher, the optimizer makes less progress per step and can step too far or not far enough.
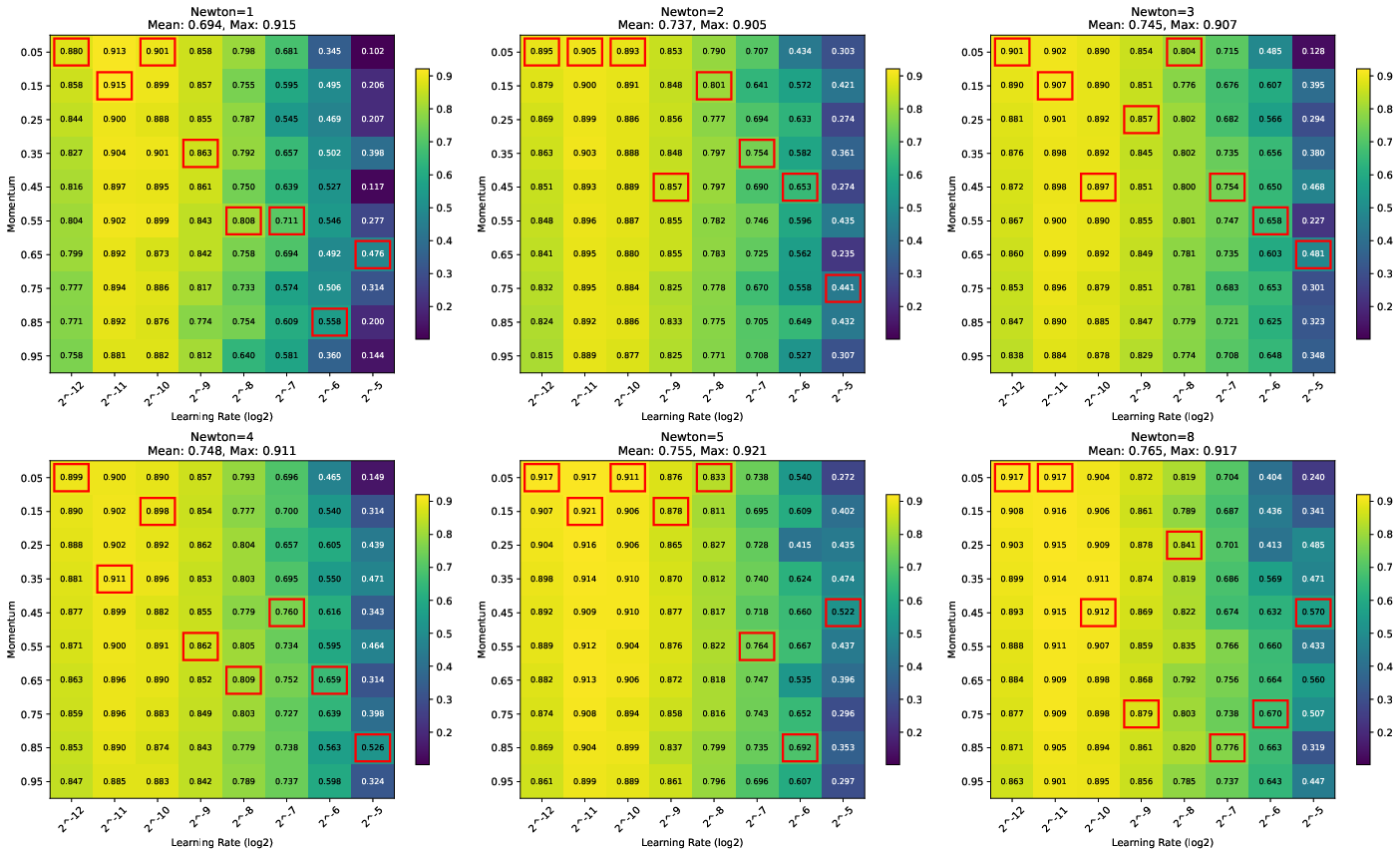
- Learn rate and momentum must co-tune with precision. When the shortcut is less precise:
- Use a smaller learning rate (to be cautious).
- Use a larger momentum (to adapt faster to noisy or slightly off directions).
- The theory matches the real algorithm. The bounds show exactly how much performance degrades based on the error. If the error is zero (perfect case), the results match earlier theory.
- Experiments confirm the predictions.
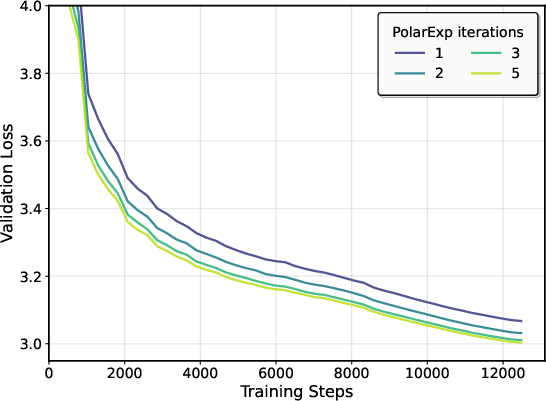
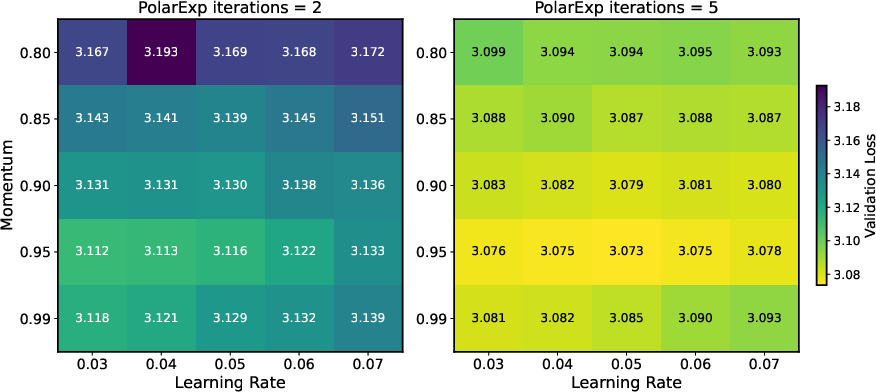
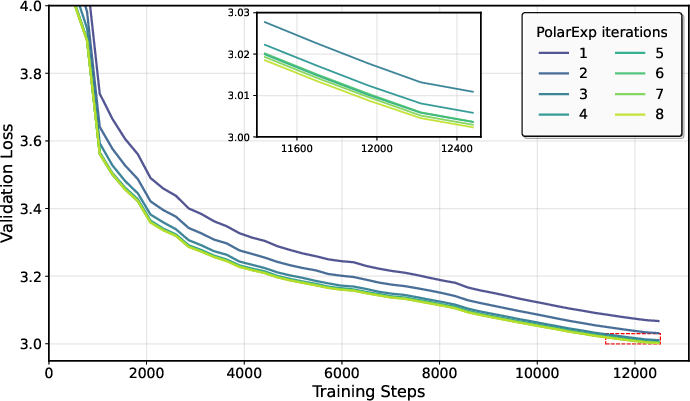
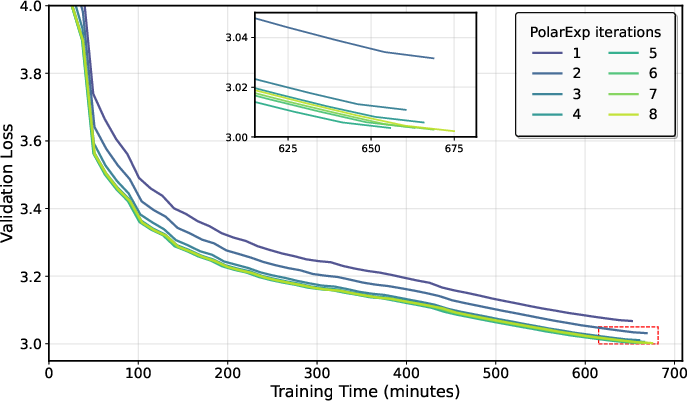
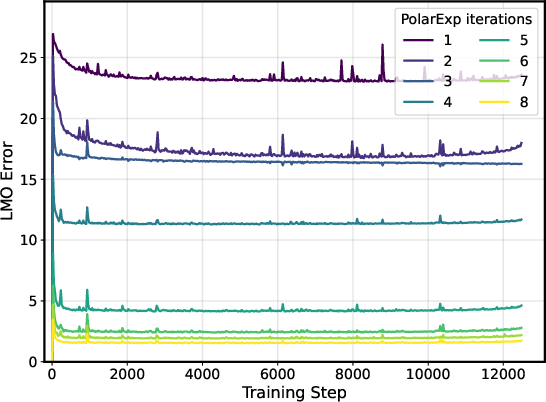
- On NanoGPT, using more PolarExpress steps (higher precision) improved validation loss and widened the safe range of learning rates.
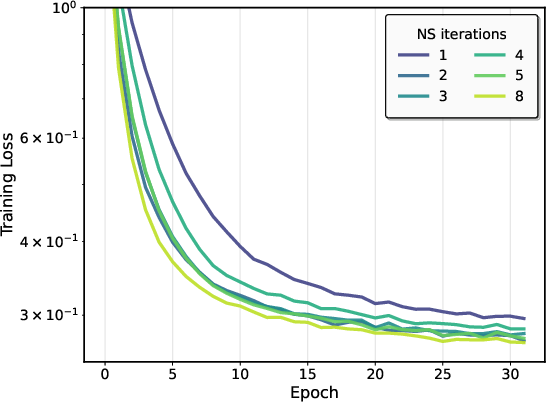
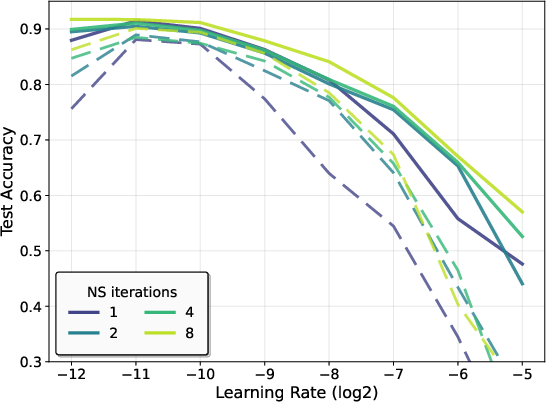
- On CIFAR-10, more Newton–Schulz steps made training faster and final accuracy better, and also made performance less sensitive to hyperparameter choices.
In short: better approximation gives better, faster training; worse approximation means you should reduce the learning rate and increase momentum.
Implications and Impact
- Approximation depth is a real hyperparameter. The number of Newton–Schulz or PolarExpress steps isn’t just a coding detail—it’s a knob you must tune along with learning rate and momentum.
- Practical training recipes: If you lower approximation precision to save compute, also lower the learning rate and raise momentum to stay stable. If you increase precision, you can likely train faster and with more stable settings.
- Smarter resource use: Different layers of a network might tolerate different precision. You could save time by using fewer approximation steps on layers that are less sensitive.
- Stronger theoretical foundation: This paper bridges the gap between ideal theory and the real Muon people use, making Muon’s success easier to understand and reproduce.
Overall, this work helps practitioners use Muon more effectively and safely, and provides clear guidance on how to tune it when using fast, approximate methods for its core operation.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a consolidated list of specific gaps and open problems left unresolved by the paper that can guide future research.
- Mapping approximation steps to ε: Derive tight, algorithm-specific bounds relating the number of Newton–Schulz/PolarExpress iterations, gradient spectrum/conditioning, normalization heuristics, and numerical precision to the additive error parameter εk in Assumption 1; provide high-probability guarantees and quantify dependence on gradient scaling.
- Alternative inexactness models: Analyze LMO errors under relative/duality-gap inaccuracies, multiplicative objective suboptimality, or angular (cosine) deviation, and determine whether the predicted hyperparameter coupling and convergence rates persist.
- Feasibility enforcement vs. theory: Study the impact of enforcing feasibility (e.g., clipping ||d̂|| to 1) on convergence bounds compared to allowing ||d̂|| ≤ 1+ε; quantify trade-offs and propose principled clipping schemes.
- Stability thresholds: Go beyond the ε<1 requirement to characterize sharp stability regions as functions of (ε, γ, α, L, σ); identify maximum safe ε and step-length conditions and design safeguards to prevent instability.
- Online co-tuning strategies: Develop practical, closed-loop rules to co-tune γk and αk based on real-time estimates of εk; propose estimators for εk that do not require SVD and paper their statistical reliability.
- Dimension dependence via ρ: Make the dependence on the norm-compatibility constant ρ explicit for common settings (e.g., spectral vs. Frobenius/nuclear norms), quantify scaling with layer shape/rank/width, and validate dimension-driven degradation empirically.
- Estimability of required constants: Provide practical methods to estimate or track L, σ2, Δ0, and ε during training to enable near-optimal parameter schedules; assess robustness when these estimates are noisy or biased.
- Non-ideal noise models: Extend the stochastic analysis beyond bounded-variance, unbiased noise to heavy-tailed, correlated, or biased gradients (e.g., due to data augmentation or mixed precision); incorporate gradient clipping or robust estimators and quantify effects on rates and ε coupling.
- Variance reduction under inexact LMO: Investigate whether variance-reduced methods (e.g., SVRG/SARAH), iterate averaging, or adaptive batch sizing can improve the O(K{-1/4}) rate with inexact LMO and how ε modifies attainable gains.
- Non-smooth and constrained objectives: Generalize the analysis to non-smooth objectives (e.g., ReLU networks) and constrained problems, including interactions with proximal operators; determine how ε enters subgradient/proximal frameworks.
- Training tricks and regularization: The theory excludes decoupled weight decay, gradient clipping, norm-scaled updates, and learning-rate schedules used in practice; analyze their interactions with inexactness and momentum coupling.
- Layer-wise precision allocation: Formalize per-layer εi selection (and per-layer γi, αi) to optimize a global compute–convergence objective; derive algorithms to allocate Newton–Schulz/PolarExpress iterations across layers given Li, curvature, or sensitivity.
- Compute–accuracy trade-offs: Provide a principled cost–benefit analysis balancing extra LMO iterations against wall-clock time and convergence improvements; derive optimal iteration counts under hardware budgets and problem constants (L, σ, Δ0).
- End-to-end guarantees for specific approximators: Prove convergence with realistic stopping rules, pre-normalization, and finite-precision arithmetic for Newton–Schulz, PolarExpress, and CANS; include mixed-precision and tensor-core effects.
- Time-varying εk schedules: Analyze adaptive precision schedules (e.g., increasing/decreasing LMO accuracy over training), and derive optimal annealing policies for εk.
- Stronger structural assumptions: Determine whether additional structure (e.g., PL condition, quasi-convexity, error bound conditions) yields faster rates under inexact LMO and how ε affects linear convergence or acceleration.
- Angle-based progress bounds: Replace ||d̂−d|| with angle/cosine similarity guarantees to capture directional alignment; compare implications for descent and hyperparameter sensitivity.
- Interaction with second-moment methods: Analyze inexact LMO when combined with Adam-like second-moment preconditioning or Shampoo-type updates; clarify whether ε–hyperparameter coupling changes.
- Gradient scaling effects: Quantify how scaling of mk or normalization layers used in practice affect εk and stability; propose normalization schemes that provably bound εk.
- Estimating L in spectral geometry: Provide practical procedures to estimate or upper bound L with respect to the spectral/nuclear norm geometry for deep networks; assess looseness and its impact on rates.
- Empirical scope and external validity: Extend experiments to larger models (e.g., multi-billion-parameter LLMs), longer training horizons, and downstream metrics (e.g., perplexity, accuracy, robustness), controlling for total compute to isolate ε effects.
- Generalization consequences: Investigate whether LMO precision influences generalization (beyond optimization speed), and whether inexactness acts as implicit regularization impacting test performance.
- Failure modes near ε→1: Characterize divergence/instability mechanisms as ε approaches 1; design detection mechanisms (e.g., monitoring ||d̂|| or progress proxies) and automatic mitigation.
- Tightness and lower bounds: Establish lower bounds that explicitly depend on ε to evaluate the tightness of the (1+ε) and 1/(1−ε) penalties; identify regimes where constants can be sharpened.
- Other expensive norms: Validate the framework and empirical findings for other expensive LMOs (e.g., group norms, path norms, Schatten-p norms) where exact oracles are costly and approximations are needed.
- Distributed and sharded training: Extend inexact analysis to distributed Muon variants with communication compression and shard-wise orthogonalization; quantify error accumulation across devices and its coupling to γ and α.
- Warm-started approximations: Analyze the benefits of warm-starting iterative LMO approximations from previous steps to reduce ε without extra cost; provide theoretical and empirical characterization.
- Monitoring and control proxies: Propose inexpensive proxies (e.g., estimates of ||d̂||, angle with mk, or duality gap surrogates) for real-time monitoring of inexactness and triggering precision/clipping adjustments with guarantees.
Practical Applications
Immediate Applications
The following applications can be deployed now, using the paper’s analysis to inform tools, training practices, and workflows.
- Precision-aware hyperparameter co-tuning for Muon and Scion optimizers in deep learning training
- What: Adjust learning rate down and momentum up as LMO approximation precision decreases; use the derived scalings (e.g., γ∝(1+ε)−1/4 and α∝√(1+ε)) to anchor sweeps.
- Sectors: Software/AI, cloud ML, LLM training (e.g., GPT-class, vision models).
- Tools/Workflow: “ε-aware” optimizer configs in PyTorch/DeepSpeed; scripting that sets safe search ranges based on iteration count of Newton-Schulz/PolarExpress.
- Assumptions/Dependencies: ε<1; approximate mapping from iteration count to ε; Lipschitz-like smoothness; unbiased stochastic gradients.
- Training recipe updates for LLMs and vision models using Muon with approximate orthogonalization
- What: Revise standard recipes to reflect the coupling—use smaller LR and larger momentum when using fewer Newton-Schulz/PolarExpress steps; prefer PolarExpress/CANS when feasible to lower ε.
- Sectors: Software/AI, education (edtech models), finance (customer support LLMs), healthcare (clinical NLP).
- Assumptions/Dependencies: Availability of Muon/Scion implementations; error bounds consistent with additive model; ε tracked via iteration count.
- Precision budgeting across layers (layer-wise allocation of approximation effort)
- What: Allocate more orthogonalization iterations to sensitive layers (e.g., attention/MLP weights), fewer to robust ones, reducing compute while maintaining stability.
- Sectors: Software/AI, energy/cost management.
- Tools/Workflow: Per-layer iteration settings; layer-wise monitoring of step norms to infer sensitivity.
- Assumptions/Dependencies: Basic layer-wise norm/smoothness differences; ability to configure per-layer iteration counts; ε heterogeneity tolerated by training.
- Stability guards in training pipelines
- What: Enforce ε<1 and cap effective step length using measured direction norm; flag when infeasible updates occur (norm > 1+ε).
- Sectors: MLOps, cloud ML.
- Tools/Workflow: Runtime checks on ||d̂|| and step norms; automatic LR back-off when infeasibility is detected.
- Assumptions/Dependencies: Access to direction norms; quick estimation of ε via iteration count.
- Cost/performance trade-off tuning for compute-limited environments
- What: Systematically reduce approximation iterations to fit memory/compute budgets and compensate with LR/momentum changes to retain acceptable performance.
- Sectors: Startups, academia, on-prem/edge training.
- Tools/Workflow: Budget-aware training scripts; templated configs for “low-precision LMO” modes.
- Assumptions/Dependencies: Clear compute budget; tolerance for modest degradation in convergence constants.
- Hyperparameter search narrowing using theory-informed ranges
- What: Use the derived scalings to narrow LR/momentum grids, speeding up sweeps and reducing cost.
- Sectors: AutoML, MLOps.
- Tools/Workflow: Bayesian search priors parameterized by ε; dashboards that visualize the predicted shift in optima.
- Assumptions/Dependencies: Rough ε estimate; standard variance assumptions; norm compatibility.
- Adoption of more accurate approximate orthogonalization methods
- What: Replace Newton-Schulz with PolarExpress or CANS when beneficial; expect tighter convergence constants due to lower ε.
- Sectors: Software/AI.
- Tools/Workflow: Drop-in kernel swaps; benchmarking harnesses comparing ε vs. wall-clock throughput.
- Assumptions/Dependencies: Kernel availability; integration with existing optimizer stacks.
- Practical guidelines for reproducibility and reporting
- What: Report LMO approximation details (algorithm, iterations), and state tuned LR/momentum ranges reflecting ε.
- Sectors: Academia, industry publishing.
- Tools/Workflow: Reproducibility checklists and artifact metadata.
- Assumptions/Dependencies: Community norms; consistent ε proxy via iteration counts.
- Reduced hyperparameter brittleness via higher precision
- What: Favor slightly more orthogonalization iterations to widen the stable LR/momentum region (as seen in NanoGPT/CIFAR experiments).
- Sectors: Software/AI, education.
- Tools/Workflow: Stability-first training presets; guardrails that suggest iteration increases when instability is detected.
- Assumptions/Dependencies: Marginal compute headroom.
- Community fine-tuning recipes for consumer GPUs
- What: Provide “low-iteration Muon” presets with conservative LR and boosted momentum for hobbyist LLM fine-tuning.
- Sectors: Daily life (open-source communities).
- Tools/Workflow: Config packs for popular repos (nanoGPT-like), with ε-aware defaults.
- Assumptions/Dependencies: Availability of Muon-like optimizers in community codebases.
Long-Term Applications
These applications require additional research, scaling, or engineering before broad deployment.
- Online ε estimation and closed-loop control
- What: Estimate approximation error during training (e.g., via randomized SVD sketches or step-norm diagnostics) and adapt LR/momentum in real-time.
- Sectors: MLOps, AutoML.
- Tools/Products: “εMonitor” service; adaptive controllers that co-tune precision and hyperparameters.
- Assumptions/Dependencies: Fast, low-overhead ε estimators; robust control logic; theoretical guarantees under time-varying ε.
- Dynamic precision scheduling under compute/energy constraints
- What: Adjust approximation iterations over training to meet time/energy budgets while maintaining convergence—raise iterations in unstable phases, reduce them when stable.
- Sectors: Energy, cloud ML cost optimization.
- Tools/Products: “Precision Budget Planner” integrated with job schedulers.
- Assumptions/Dependencies: Reliable instability signals; energy metering APIs; ε<1 maintained.
- Layer-wise sensitivity learning and meta-optimization
- What: Learn per-layer ε allocations via meta-learning/RL to maximize accuracy at fixed compute.
- Sectors: Software/AI, AutoML.
- Tools/Products: “LayerWise Precision Allocator” that outputs per-layer iteration plans.
- Assumptions/Dependencies: Differentiable proxies for sensitivity; stable training with heterogeneous ε.
- Hardware/software co-design for fast polar approximation
- What: Specialized kernels/accelerators for Newton-Schulz/PolarExpress (e.g., fused matmul pipelines) reducing ε at fixed cost.
- Sectors: Semiconductors, cloud ML accelerators.
- Tools/Products: Library support in cuBLAS/ROCm; vendor-specific primitives.
- Assumptions/Dependencies: Vendor adoption; algorithm/hardware co-optimization.
- Adaptive optimizers that co-optimize LR, momentum, and LMO precision
- What: New optimizers that treat approximation quality as a first-class parameter with schedules/policies guided by theory.
- Sectors: Software/AI.
- Tools/Products: “MuonTuner” optimizer family with ε-aware schedulers.
- Assumptions/Dependencies: Stability and convergence guarantees under joint adaptation; robust estimation of variance σ and smoothness L.
- Extensions to distributed and compressed training with inexact LMOs
- What: Combine error-feedback, communication compression, and ε-aware analysis to scale training efficiently.
- Sectors: Cloud ML, edge-distributed AI.
- Tools/Products: EF21-Muon-like frameworks generalized to inexact LMOs; compression-aware ε control.
- Assumptions/Dependencies: Network variability; synchronization strategies; extended theory for distributed noise.
- Broximal/trust-region inspired algorithms with efficient inexact solvers
- What: Design practical approximations of non-Euclidean BPM that preserve finite-step or improved rates in deep learning contexts.
- Sectors: Academia, software/AI.
- Tools/Products: Trust-region variants with spectral-norm geometry and inexact oracles.
- Assumptions/Dependencies: New theory bridging BPM and inexact LMOs; scalable implementations.
- Standards and policy for compute-efficient training reporting
- What: Encourage reporting of approximation precision and ε-aware tuning for transparency and energy accountability.
- Sectors: Policy, ESG, industry governance.
- Tools/Products: Standards in model cards; audit frameworks linking ε choices to energy use.
- Assumptions/Dependencies: Community buy-in; measurable links between ε and energy.
- Energy-aware training that integrates grid constraints
- What: Vary approximation precision (and thereby compute draw) in response to grid signals/carbon intensity without derailing convergence.
- Sectors: Energy, sustainability.
- Tools/Products: Grid-integrated ML schedulers; carbon-aware ε and LR/momentum policies.
- Assumptions/Dependencies: Real-time energy APIs; resilience under nonstationary resource limits.
- Better modeling (L0/L1 smoothness, block-wise norms) for heterogeneous networks
- What: Use generalized smoothness and block-wise ε to tailor training for architectures with heterogeneous layers (e.g., transformers with varied smoothness).
- Sectors: Software/AI, robotics (perception/control stacks).
- Tools/Products: Model-aware optimizer presets; architecture-specific ε maps.
- Assumptions/Dependencies: Accurate smoothness proxies; validation across tasks and sectors.
Glossary
- Additive error model: A formal assumption that the oracle’s output deviates from the exact solution by a bounded additive amount. "introducing a realistic additive error model to capture the inexactness of practical approximation schemes."
- AdamW: A widely used adaptive optimizer with decoupled weight decay for training deep networks. "The {Muon} optimizer has rapidly emerged as a powerful, geometry-aware alternative to {AdamW}"
- Ball-proximal point method (BPM): A trust-region-like method that solves proximal subproblems constrained to a norm ball, with strong convergence guarantees. "An idealized trust-region method, called the ball-proximal (``broximal'') point method ({BPM})"
- Bounded variance: An assumption that the variance of the stochastic gradient estimator is uniformly upper bounded. "and has a uniformly bounded variance, "
- Broximal operator: The operator associated with BPM’s ball-proximal step, used analogously to the proximal operator but over a ball. "where the broximal operator is applied to a stochastic linear approximation of the loss"
- CANS: An iterative scheme for faster or more accurate polar-factor approximation used in Muon-like updates. "and {CANS} \citep{grishina2025accelerating}, which offer better error guarantees or faster convergence."
- Communication compression: Techniques that reduce communication payload in distributed optimization by compressing messages. "with support for communication compression, error-feedback and generalized smoothness"
- Dual norm: The norm defined by the supremum of inner products over unit vectors in the primal norm, used to measure gradients. "where is the dual norm of ."
- EF21-Muon: A distributed variant of Muon that incorporates error-feedback and compression mechanisms. "who proposed the {EF21-Muon} method."
- Error-feedback: A mechanism in distributed optimization that accumulates and re-injects compression errors to preserve convergence. "with support for communication compression, error-feedback and generalized smoothness"
- Frank-Wolfe algorithm: A projection-free first-order optimization method relying on a Linear Minimization Oracle. "the Frank-Wolfe algorithm~\citep{frank1956algorithm}"
- Geometric preconditioning: Choosing a geometry (norm) to implicitly precondition optimization dynamics. "with the non-Euclidean norm playing the role of a hyper-parameter performing a form of geometric preconditioning."
- Gradient drift: The change in the gradient across iterations due to parameter movement, which must be controlled in analysis. "the ``gradient drift'' term"
- Inexact LMO: A Linear Minimization Oracle that returns an approximate solution with bounded error rather than an exact minimizer. "Assume the inexact LMO satisfies Assumption~\ref{assump:inexact_lmo_main}"
- Iteration complexity: The number of iterations required to achieve a target stationarity or accuracy level. "implies an iteration complexity of "
- LLMs: Very large neural networks trained to model language distributions and perform NLP tasks. "state-of-the-art LLMs"
- Layer-wise setting: An analysis or algorithmic setup where each model layer (or block) is treated with its own norm, smoothness, or update rule. "a more realistic layer-wise setting"
- Linear Minimization Oracle (LMO): An oracle that returns the minimizer of a linear functional over a constraint set, typically a unit ball. "Linear Minimization Oracle (LMO)-based optimization"
- Lipschitz continuity (L-smoothness): A smoothness condition stating that the gradient changes at most linearly with respect to the chosen norm. "its gradient is Lipschitz continuous with constant "
- (L0, L1)-smoothness model: A generalized smoothness framework parameterized by two constants capturing non-Euclidean smoothness. "the -smoothness model"
- Momentum (optimization): An exponential moving average of gradients used to stabilize and accelerate stochastic optimization. "the momentum parameter"
- Muon: A matrix-aware, geometry-driven optimizer that uses orthogonalized directions under spectral norm geometry. "The {Muon} optimizer has rapidly emerged as a powerful, geometry-aware alternative to {AdamW}"
- NanoGPT: A compact GPT-style LLM used as a standard benchmark for training experiments. "NanoGPT experiments directly confirm the predicted coupling"
- Newton–Schulz iteration: An iterative, SVD-free method for approximating the polar factor (or matrix inverse square root) via matrix multiplications. "the {Newton-Schulz} iteration"
- Non-Euclidean norm: A norm different from the Euclidean norm, used to define alternative geometries for optimization. "with the non-Euclidean norm playing the role of a hyper-parameter"
- Non-Euclidean trust-region: A trust-region approach defined under non-Euclidean norms, offering geometry-aware updates. "developed a non-Euclidean trust-region interpretation"
- Norm compatibility condition: A relationship bounding one norm (e.g., dual norm) in terms of another (e.g., Euclidean), used to connect variance assumptions to the analysis. "we assume a norm compatibility condition"
- Orthogonal polar factor: The unitary/orthogonal component in a matrix’s polar decomposition. "The solution to \eqref{eq:steepest_descent} is the orthogonal polar factor of the negative gradient"
- Orthogonalization oracle: A hypothetical subroutine that returns an exact orthogonalized direction (e.g., via SVD), used in idealized analyses. "assume access to an exact orthogonalization oracle"
- Orthogonalized update: An update direction normalized or projected to the orthogonal (unitary) factor consistent with spectral geometry. "the inexact orthogonalized update at {Muon}'s core"
- Polar decomposition: A matrix factorization into a unitary/orthogonal factor and a positive-semidefinite factor. "approximate the orthogonal factor of a matrix's polar decomposition"
- PolarExpress: An iterative algorithm designed to approximate the polar factor with fast convergence. "the {PolarExpress} algorithm~\citep{amsel2025polar}"
- Scion framework: A general framework that places Muon within LMO-based methods and provides convergence guarantees. "introduced the {Scion} framework"
- SignSGD: A variant of SGD that uses the sign of the gradient, often associated with geometry. "such as the norm in {SignSGD}"
- Singular Value Decomposition (SVD): A factorization of a matrix into orthogonal matrices and singular values, used for exact orthogonalization. "avoiding a full Singular Value Decomposition (SVD)"
- Spectral descent: Optimization that follows steepest descent under the spectral norm geometry. "The concept of spectral descent and orthogonalized updates has historical roots"
- Spectral norm: The operator norm of a matrix equal to its largest singular value, defining the geometry for Muon’s updates. "the unit ball with respect to the spectral norm."
- Spectral norm geometry: The optimization geometry induced by the spectral norm, shaping descent directions. "with respect to the spectral norm geometry"
- Steepest descent: The direction that minimizes the inner product with the gradient over the unit ball of a given norm. "this update is equivalent to performing steepest descent with respect to the spectral norm geometry"
- Stochastic first-order oracle (unbiased): An oracle returning an unbiased estimate of the gradient, typically with bounded variance. "we assume access to an unbiased stochastic first-order oracle with bounded variance."
- Trust-region method: An optimization strategy restricting steps to a neighborhood (trust region) where local models are reliable. "An idealized trust-region method"
Collections
Sign up for free to add this paper to one or more collections.