SimKO: Simple Pass@K Policy Optimization (2510.14807v2)

Abstract: Reinforcement learning with verifiable rewards (RLVR) has advanced the reasoning capabilities of LLMs. However, prevailing RLVR methods exhibit a systematic bias toward exploitation over exploration, as evidenced by improved pass@1 but reduced pass@K (K>1) performance. To understand this issue, we analyze training dynamics of RLVR methods by tracking the token-level probability distributions over vocabulary candidates. Our analysis reveals a consistent probability concentration effect where the top-1 candidate increasingly accumulates probability mass and suppresses that of other candidates. More importantly, stronger over-concentration correlates with worse pass@K performance. Inspired by this finding, we propose Simple Pass@K Optimization (SimKO), a method designed to mitigate the over-concentration issue, thereby encouraging exploration. SimKO operates in an asymmetrical manner. For verified-correct responses, it boosts the probabilities of the top-K candidates. For verified-incorrect responses, it applies stronger penalties to the top-1 candidate. We observe that this asymmetric design is particularly effective at mitigating over-concentration when applied at tokens with high entropy. Across various math and logical-reasoning benchmarks, SimKO consistently yields higher pass@K for a wide range of K, providing a simple way to improve RLVR's exploration.

• The paper introduces SimKO, a technique that redistributes gradient updates across top-K candidates to mitigate over-concentration on the top-1 token.
• It enhances token-level exploration by applying asymmetric penalties to incorrect top-1 responses while boosting correct candidate probabilities.
• Experimental results show SimKO outperforms baselines on math and logic benchmarks, offering a balanced improvement in pass@1 and pass@K metrics.

SimKO: Simple Pass@K Policy Optimization

Introduction and Motivation

In the field of reinforcement learning with verifiable rewards (RLVR), the reasoning capabilities of LLMs have traditionally prioritized exploitation over exploration. This focus often enhances pass@1 performance but diminishes pass@K outcomes (where K > 1), indicating a deficiency in exploring multiple reasoning paths. The core challenge is the over-concentration of probability mass on the top-1 candidate during training, which restricts the model's ability to generalize and innovate beyond familiar scenarios.

Methodology: SimKO

SimKO (Simple Pass@K Optimization) introduces an asymmetric strategy to tackle the over-concentration observed in RLVR methods. This approach is characterized by enhancing probabilities of the top-K candidates for correct responses, and applying stronger penalties to the top-1 candidate for incorrect responses, especially at high-entropy tokens.

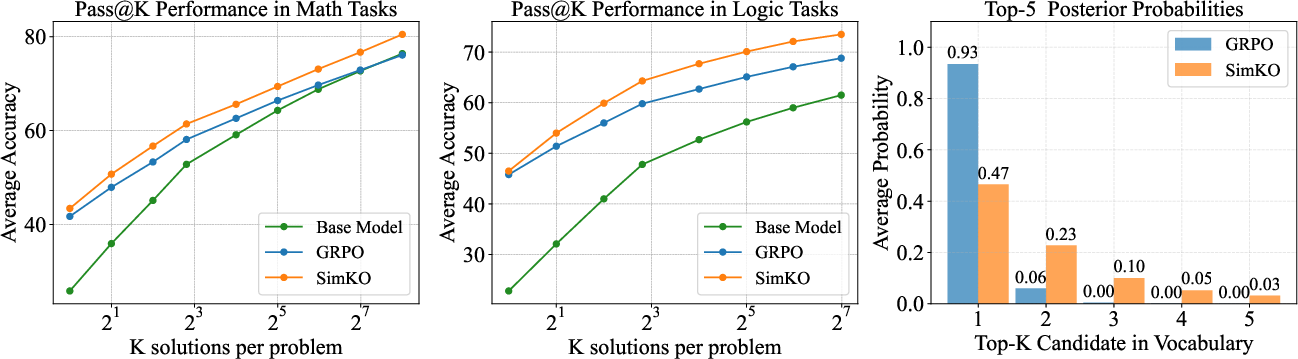
Figure 1: SimKO improves pass@K performance on math and logic tasks, compared to GRPO, with a broader probability distribution.

Key Components

1. Exploration Behavior: The model’s token-level probability distribution is monitored, revealing a skew towards the top-1 candidate. Proper exploration necessitates a more equitable distribution among high-entropy tokens.
2. Distribution Mitigation: For correct responses, SimKO redistributes gradient updates across top-K candidates, reducing over-concentration on a single choice. For incorrect responses, repositioning of probabilities discourages sharp, deterministic distributions, fostering broader exploration.

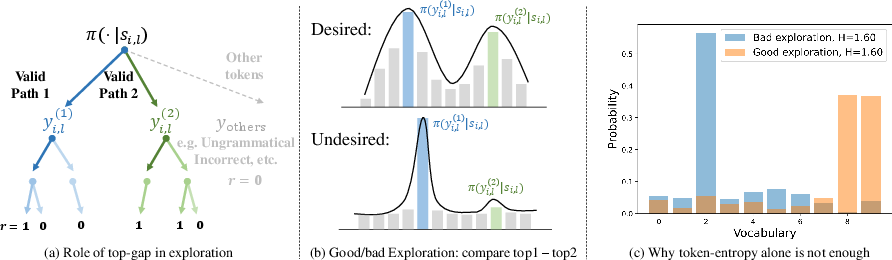
   Figure 2: Visualization of the exploration behavior and comparison of exploration strategies.

Implementation and Results

Redistribution Mechanism

SimKO employs label smoothing modified for the top-K candidates, ensuring that gradient updates prevent all probability mass from concentrating on a single candidate. This mechanism is elegantly implemented with adjustments to the policy gradient calculations:

def compute_policy_loss(): ratio = torch.exp(log_prob - old_log_prob) # 1. Identify high-entropy tokens w = (entropy > percentile(entropy, τ)) # 2. Utilize top-K ratio for positive samples topk_ratio = torch.exp(topk_log_probs - old_topk_log_probs).sum(dim=-1) ratio = torch.where(advantage > 0, (1-α*w)*ratio + (α*w/K)*topk_ratio, ratio) # 3. Apply stronger penalties to top-1 negative tokens mask = (advantage < 0) & is_top1 & w ratio[mask] *= λ pg_losses = -advantage * ratio

Experimental Validation

SimKO consistently outperformed baseline methods across several math and logic benchmarks. These improvements were characterized by enhancements in both exploitation (pass@1) and exploration (pass@K) metrics.

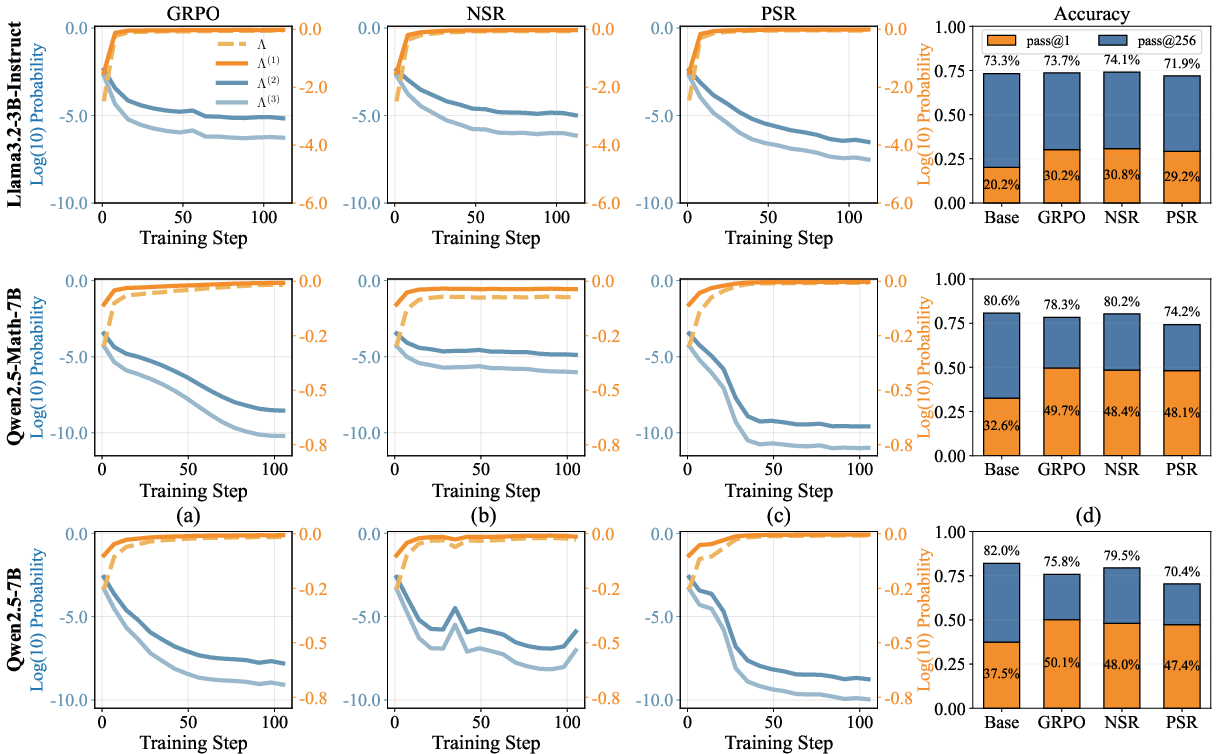
Figure 3: Comparison of SimKO with GRPO, KL-Cov, Entropy-Adv, demonstrating SimKO's effective control of probability concentration.

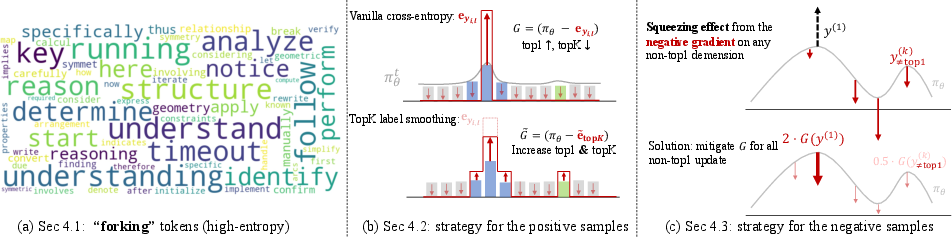
Figure 4: Entropy distributions showing SimKO's ability to maintain entropy in "forking" tokens.

SimKO's ability to balance between top-1 exploitation and broader exploration was validated through experiments on various competitive frameworks, consistently showing a superior balance across datasets.

Concluding Remarks

SimKO provides a strategic advancement in rectifying the exploration bias present in RLVR by leveraging a detailed analysis of token-level distributions. This methodology not only mitigates probability collapse but also fortifies the model's capacity to discern and pursue multiple correct reasoning paths. The promising results showcase a notable enhancement in the model's decision-making framework, paving the way for future enhancements in model exploration dynamics.