Entropy Regularizing Activation: Boosting Continuous Control, Large Language Models, and Image Classification with Activation as Entropy Constraints (2510.08549v1)
Abstract: We propose ERA, a new paradigm that constrains the sampling entropy above given thresholds by applying specially designed activations to the outputs of models. Our approach demonstrates broad effectiveness across different domains: 1) for LLMs(LLMs), boosting the AIME 2025 score for Qwen2.5-Math-7B by 37.4%; 2) for continuous control reinforcement learning agents, improving performance by more than 30% over strong baselines such as SAC on the challenging HumanoidBench; 3) for image classification, enhancing ImageNet top-1 accuracy by 0.69% for ResNet-50. These gains are achieved with a computational overhead of less than 7%. Our work validates output activation as a powerful tool for entropy control, opening a new direction for designing simpler and more robust algorithms.
Summary
- The paper introduces ERA, a novel activation function that decouples entropy regularization from the main loss, enabling more stable optimization across domains.
- Key methodological innovations include analytically derived activations for continuous control, softmax classifiers, and token-level LLM RL with rigorous theoretical guarantees.
- Empirical results demonstrate over 30% improvement in RL, enhanced LLM reasoning accuracy, and boosted image classification performance with minimal computational overhead.
Entropy Regularizing Activation: A Unified Paradigm for Entropy-Constrained Training Across RL, LLMs, and Vision
Introduction and Motivation
The paper introduces Entropy Regularizing Activation (ERA), a novel architectural approach for enforcing entropy constraints in neural network-based decision-making systems. Unlike traditional methods that inject entropy bonuses directly into the loss function—thereby altering the optimization landscape and potentially causing gradient conflicts—ERA imposes entropy constraints via specially designed activation functions at the model output layer. This decouples entropy regularization from the primary objective, enabling more stable and theoretically grounded training across diverse domains: continuous control in RL, LLM alignment, and image classification.
Figure 1: ERA consistently improves performance in LLMs, RL continuous control, and image classification, demonstrating broad applicability and effectiveness.
Methodology: ERA as Output Activation
General Framework
ERA operates by transforming the output distribution parameters of a model via an activation function , such that the resulting policy satisfies a minimum expected entropy constraint:
This architectural constraint ensures that the optimization of model parameters is focused solely on the primary objective (e.g., reward maximization), with entropy regularization handled orthogonally.
Instantiations
- Continuous Control (Bounded Gaussian Policies):
ERA adjusts the standard deviation of the Gaussian policy such that the entropy of the squashed or truncated Gaussian remains above . The activation function is derived analytically to guarantee this lower bound, compensating for the entropy loss due to bounding operations (e.g., or truncation). The compensation parameter can be learned via dual optimization, ensuring strong duality and convergence.
- Discrete Classification (Softmax Policies):
For softmax-based classifiers, ERA transforms logits such that the output distribution's entropy is at least . The transformation leverages a monotonic mapping between entropy and probability, using a scaling factor to ensure invertibility and normalization. This approach generalizes label smoothing, allowing input-dependent uncertainty allocation.
- LLM RL (Token-Level Entropy):
In LLM RL, ERA is applied post-sampling, modifying the logits of sampled tokens during policy updates. The method adaptively sharpens or flattens the distribution for tokens with positive advantage, based on the entropy of the top 20% "forking" tokens in the response. This prevents entropy collapse and maintains exploration without corrupting deterministic tokens, a critical property for natural language generation.
Theoretical Guarantees
The paper provides formal proofs that ERA enforces a strict entropy lower bound in both continuous and discrete settings. For continuous control, the entropy of the final policy is shown to be at least plus a compensation term, with bounded for stability. For discrete policies, the mapping ensures that the entropy after normalization remains above the target. In LLM RL, the adaptive KL regularization induced by ERA guarantees that the response entropy does not collapse, under mild assumptions on advantage distribution and entropy dynamics.
Empirical Results
Continuous Control
ERA is integrated into SAC, PPO, TD-MPC2, OBAC, and FastSAC across challenging benchmarks (HumanoidBench, DMC, Mujoco Gym). ERA consistently accelerates learning and achieves superior asymptotic performance, with improvements exceeding 30% over strong baselines in high-dimensional tasks.
Figure 2: ERA accelerates learning and improves final performance across multiple RL algorithms and benchmarks.
ERA demonstrates robustness to the minimum entropy hyperparameter, outperforming SAC across a wide range of entropy values.
Figure 3: ERA maintains superior performance and accuracy across varying minimum entropy constraints in RL and vision tasks.
Image Classification
ERA is applied to ResNet-50 on ImageNet and CIFAR-10, both with and without data augmentation. It consistently boosts top-1 and top-5 accuracy, outperforming label smoothing and dropout regularization. The method introduces negligible computational overhead.
LLM RL
ERA is evaluated on Qwen2.5-Math-7B and 1.5B, trained with GRPO and GSPO on mathematical reasoning benchmarks (AIME'24, AIME'25, AMC, MATH500, Minerva, OlympiadBench). ERA yields strong improvements, e.g., a 37.4% increase on AIME'25 and 9.8% average gain across benchmarks, outperforming KL-Cov, Clip-Cov, and other entropy-control methods.
ERA prevents entropy collapse, maintaining a stable entropy floor and enhancing pass@ reasoning capacity.
Figure 4: ERA mitigates entropy collapse in LLM RL, resulting in higher entropy and improved pass@ reasoning scores.
ERA also improves out-of-distribution generalization, with a 16.9% average gain on ARC-C, GPQA-Diamond, and MMLU-Pro.
Implementation and Efficiency
ERA is implemented as a lightweight activation function at the output layer, requiring no additional networks or complex training procedures. The computational overhead is minimal: less than 7% in RL and less than 6% in LLM RL, with virtually no overhead in vision tasks. The method is compatible with existing frameworks (JAXRL, timm, verl) and can be integrated with minimal code changes.
Comparative Analysis and Ablations
- Policy Distribution Stability:
Truncated Gaussian policies with ERA are more stable than Tanh-squashed Gaussians, especially when learning the compensation parameter .
- Batch vs. State-Level Regularization:
Both batch-level and state-level entropy regularization via ERA outperform SAC, with minimal difference in locomotion-dominated tasks.
- Comparison with Maximum Entropy RL Methods:
ERA outperforms EAPO and MNSE on Mujoco Gym, with lower computational cost and no need for extra critic or dynamics networks.
- Regularization in Vision:
ERA surpasses label smoothing and dropout, providing more flexible and effective entropy control.
Implications and Future Directions
ERA establishes a unified, theoretically grounded paradigm for entropy-constrained training, applicable across RL, LLMs, and vision. By decoupling entropy regularization from the loss function, ERA avoids gradient conflicts and enables more robust optimization. The method's generality and efficiency suggest broad utility in domains where exploration, uncertainty, and generalization are critical.
Potential future directions include:
- Extending ERA to multi-agent RL and hierarchical policies.
- Investigating adaptive entropy scheduling for curriculum learning.
- Applying ERA to generative modeling and uncertainty quantification in scientific domains.
- Exploring the interaction of ERA with other regularization and exploration strategies in large-scale distributed training.
Conclusion
ERA provides a principled, efficient, and domain-agnostic solution for entropy regularization in neural decision-making systems. Its architectural approach yields strong empirical gains, theoretical guarantees, and practical scalability, marking a significant advance in the design of robust learning algorithms for RL, LLMs, and computer vision.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper introduces a simple idea called ERA (Entropy Regularizing Activation). Its goal is to keep AI models from becoming too “certain” too quickly. It does this by gently forcing a minimum level of randomness (called “entropy”) in the model’s choices. ERA works like a safety guard placed at the very end of a model, just before it makes a decision. The authors show that this trick helps in three different areas:
- Robots and control (continuous actions)
- LLMs trained with reinforcement learning
- Image classification
They also prove that ERA can guarantee a lower bound on entropy and report strong results with less than 7% extra compute.
What problem is this solving?
AI systems often need to explore options rather than always pick the most confident choice. That exploration is measured by “entropy” (more entropy = more exploring). Many current methods try to increase entropy by changing the training objective (for example, adding a bonus to reward “being random”). But that can mess with the model’s main goal and cause instability.
In LLM training with reinforcement learning (RL), there’s another common problem: “entropy collapse.” The model becomes too sure of a few answers, stops exploring other ideas, and performance stalls. Previous fixes are often specific hacks that don’t guarantee minimum entropy and don’t generalize well to other tasks.
ERA is a general, simple, and principled way to keep entropy high enough without changing the main loss function.
Key questions the paper asks
- Can we control how “exploratory” a model is (its entropy) without changing its main training goal?
- Can one method work across very different tasks: controlling robots, training LLMs, and classifying images?
- Can we do this with theoretical guarantees and small compute overhead?
How ERA works (in simple terms)
Think of a model like a student who has to pick answers from multiple choices. If the student always picks the same answer with full confidence, they won’t learn new strategies. ERA is like a teacher who says: “Keep your options open—you must consider at least a few choices.” ERA enforces this by adding a small “activation” layer right at the output that reshapes the model’s probabilities so they’re never too sharp (too certain) or too flat, depending on what’s needed.
The core idea
- “Entropy” = how spread out a model’s choices are. High entropy = more exploration.
- Instead of adding an entropy bonus in the loss (which can interfere with learning), ERA changes the model’s output probabilities using a special activation function. This activation guarantees that the model maintains at least a certain amount of entropy.
- This keeps training focused on the main goal (like maximizing reward), while the activation quietly enforces a “minimum randomness rule.”
For continuous control (e.g., robots)
- Robots choose continuous actions (like how much to bend a joint). These choices often come from a “bell curve” (Gaussian).
- ERA widens or narrows this bell curve to ensure the actions aren’t too predictable, keeping exploration alive.
- This lets the robot learn better without adding extra entropy terms into the loss function. It’s cleaner and more stable.
For image classification (discrete choices)
- A classifier turns its final scores (logits) into probabilities with softmax.
- If it’s too confident, it may overfit. ERA reshapes these logits so the model keeps a healthy amount of uncertainty, similar to label smoothing—but smarter, because it can adapt per input rather than applying a fixed rule.
For LLMs trained with RL (special case)
- LLMs pick one token at a time from a huge vocabulary. Most tokens in a sentence are almost deterministic (like punctuation or common words), so forcing high entropy for all tokens can harm quality.
- ERA for LLMs only regularizes the “forking” tokens—the top 20% most uncertain ones where the model’s reasoning can branch.
- Another key twist: ERA doesn’t change how the model samples text. It only applies during the model update step, by reinterpreting the sampled tokens with a slightly adjusted distribution. This keeps inference stable but still prevents entropy collapse during training.
- The method uses thresholds to decide when to sharpen or soften probabilities so that the overall response maintains a healthy entropy range.
Main results
Across three domains, ERA delivers consistent gains with under 7% extra compute:
- LLMs:
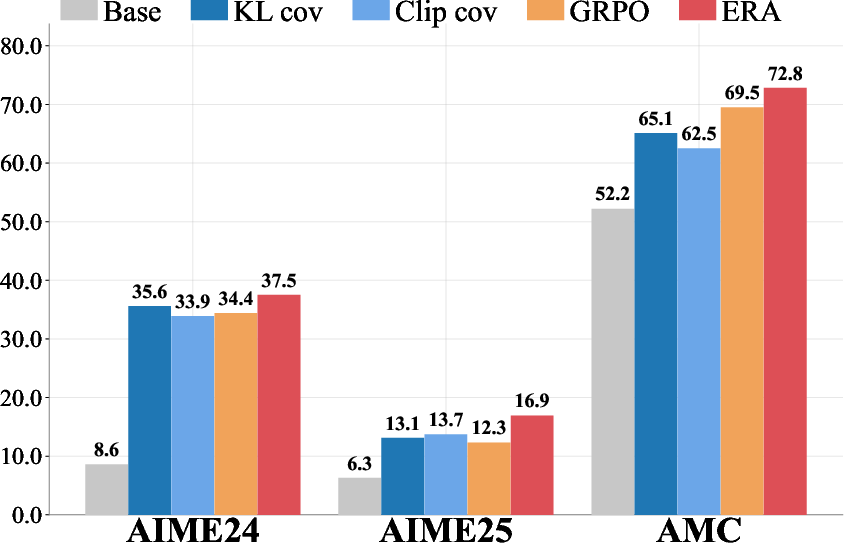
- On Qwen2.5-Math-7B, ERA improved AIME’25 score by 37.4% and AIME’24 by 9.0% over strong baselines.
- It beat other entropy-control methods (like KL-based ones), reduced entropy collapse, improved “pass@k” reasoning results, and generalized better to out-of-distribution tasks.
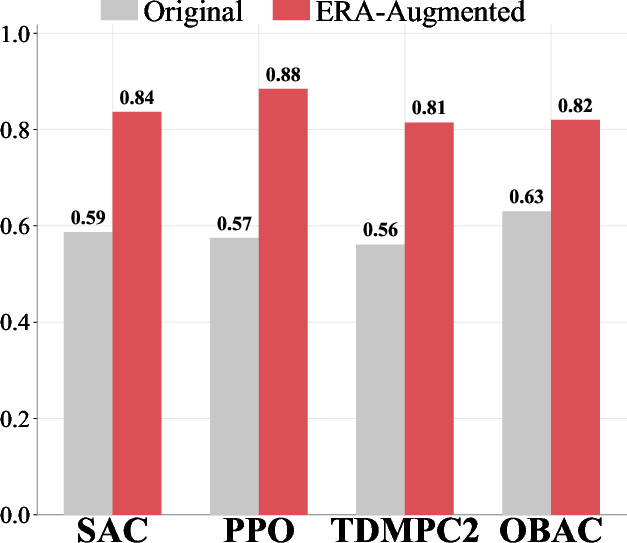
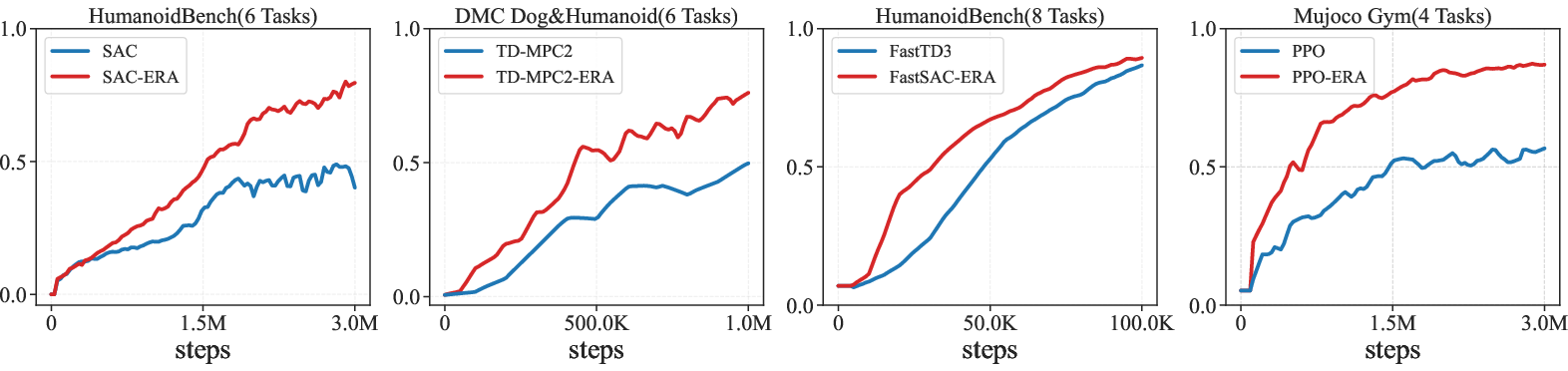
- Continuous Control (Robotics):
- On tough benchmarks like HumanoidBench and DeepMind Control Suite, ERA improved performance by over 25–30% compared to strong methods like SAC and others.
- It worked across several different RL algorithms and was less sensitive to hyperparameter tuning.
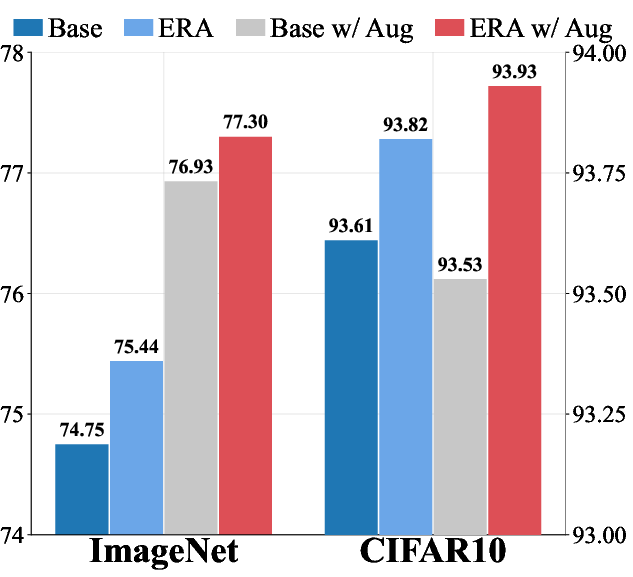
- Image Classification:
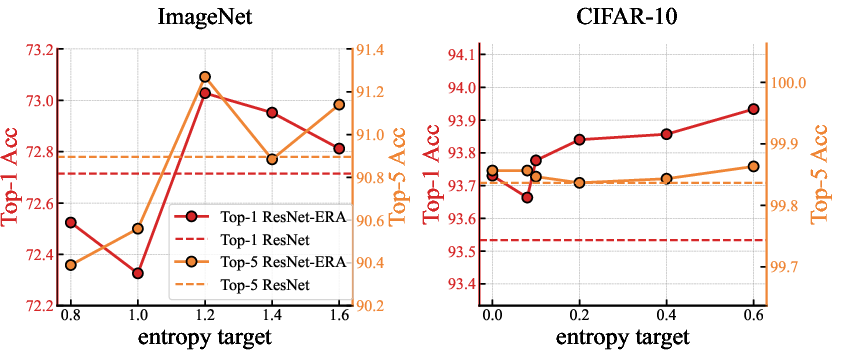
- On ImageNet with ResNet-50, ERA increased top-1 accuracy by 0.69% and also brought small but consistent gains with and without data augmentation.
- It played nicely with existing regularizers like label smoothing.
Why these results matter:
- Better exploration avoids getting stuck in narrow strategies.
- ERA’s “output-level” control avoids conflicts inside the main loss and tends to be more stable.
- It’s a single, general tool that works across very different problems.
Why this matters (impact and implications)
- General and simple: ERA offers a unified, plug-in way to control entropy across many tasks without redesigning the training objective.
- Stable and principled: It comes with theoretical guarantees of a minimum entropy, helping avoid entropy collapse (especially in LLM RL).
- Better learning and generalization: Encouraging the right amount of exploration leads to stronger performance and better transfer to new tasks.
- Practical: Works with small overhead and plays well with existing methods (like label smoothing in vision or standard RL algorithms in control).
In short, ERA turns entropy control into a clean architectural feature rather than a delicate loss-balancing act. This can make future AI systems simpler to train, more robust, and better at exploring—and therefore better at learning.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, consolidated list of concrete issues the paper leaves unresolved. Each item is phrased to guide follow-up research.
- Formal conditions for guaranteed entropy bounds: Precisely state the assumptions under which ERA ensures a minimum entropy (e.g., independence of action dimensions, bounded support, logit scaling properties), and provide tight state-wise (not only expected) bounds for tanh-squashed and truncated Gaussians.
- Quantifying the “bounding bias” and compensation δ: Derive a principled, closed-form characterization of the entropy loss due to squashing/clipping and the required compensation δ as a function of and bounds, rather than tuning δ by a residual loss.
- Validity of removing entropy terms in SAC: Analyze the theoretical and empirical consequences of eliminating the entropy bonus from the actor and critic updates (Eqs. 12–13), including effects on value over/underestimation, stability, and convergence guarantees.
- Applicability to correlated and non-Gaussian policies: Extend ERA beyond diagonal Gaussians to full covariance matrices and richer policy classes (mixtures, normalizing flows), and design activations that respect correlations across action dimensions.
- Numerical stability and differentiability of the discrete activation: Investigate gradient behavior, conditioning, and numerical issues for the softmax-based ERA (use of and its approximation), especially under large vocabularies and extreme logit scales.
- Calibration and uncertainty quality in vision: Measure expected calibration error (ECE), negative log-likelihood, and coverage to determine whether ERA improves calibrated confidence or only accuracy; assess behavior under distribution shift.
- Sampling–training mismatch in LLMs: Provide a rigorous analysis of the bias/variance and convergence of updates when training uses ERA-adjusted logits () but sampling uses the original logits (); clarify whether this remains on-policy in the PG sense.
- Theoretical guarantees for the LLM variant: Make explicit the assumptions and bounds under which the piecewise logit scaling (with , , , and “top 20% tokens”) enforces a response-level entropy floor; characterize failure cases and the exact form of the guaranteed lower bound.
- Heuristic choice of “top 20% forking tokens”: Validate or replace the fixed 20% threshold with data-driven or adaptive criteria; quantify sensitivity of results to this fraction across tasks and domains.
- Hyperparameter sensitivity and auto-tuning: Systematically paper the sensitivity and interactions of , , , minimal entropy , and δ; propose robust auto-tuning or meta-learning schedules for entropy targets.
- Generalization breadth: Evaluate ERA on larger LLMs (e.g., ≥70B), non-math reasoning, multilingual datasets, and longer sequence lengths; extend OOD analyses to vision (e.g., ImageNet-C) and control (e.g., domain randomization, dynamics shift).
- Interaction with standard regularizers: Quantify synergies/conflicts with label smoothing strength, temperature scaling, dropout, mixup/cutmix, KL penalties (e.g., PPO-style KL), and intrinsic motivation terms; identify regimes where ERA is complementary or redundant.
- Exploration vs. exploitation late in training: Determine whether enforcing a minimum entropy impedes convergence to low-entropy optimal policies; design schedules or state-dependent entropy targets to relax constraints when exploitation is preferred.
- Safety-critical and constrained RL: Test ERA in robotics/control tasks with safety constraints, contact-rich dynamics, and actuator limits; measure action saturation, failure rates, and stability under enforced entropy.
- Compute and memory overhead transparency: Provide detailed breakdowns of ERA’s runtime and memory costs across domains (LLM sequence lengths, vocabulary sizes; control/model-free vs. model-based RL; vision batch sizes), beyond the headline “<7%”.
- Robustness to noisy rewards and adversarial inputs: Assess whether entropy constraints improve or harm robustness in RL (noisy or sparse rewards) and vision (adversarial examples, corruptions).
- Analytical comparison with Lagrangian methods: Characterize when ERA and entropy-regularized objectives (e.g., SAC’s dual formulation) are equivalent or diverge; identify conditions where activation-based constraints are provably superior/inferior.
- ERA for multimodal outputs and structured prediction: Explore extensions to segmentation/detection, autoregressive vision models, and structured actions (e.g., discrete-continuous hybrids), including activation designs that control joint entropy.
- Credit assignment in long sequences (LLMs): Study how ERA affects gradient propagation, PPO/GRPO clipping dynamics, and variance in long-horizon token sequences; analyze the impact on pass@ beyond short prompts.
- Practical reproducibility in LLM experiments: Report seeds, variance, and statistical significance for LLM benchmarks; release trained checkpoints and full training scripts to substantiate large reported gains (e.g., +37.4% AIME-25).
- Numerical edge cases and implementation safety: Audit ERA’s formulas (max/log/exp/softmax weighting, inverse functions) for overflow/underflow and precision issues; provide stable, bounded implementations and backpropagation-safe variants.
Practical Applications
Practical Applications of ERA (Entropy Regularizing Activation)
ERA is a plug-in activation that enforces a minimum entropy constraint at a model’s output layer, decoupling entropy control from the loss. The paper demonstrates consistent gains with <7% overhead across three domains: continuous-control RL (e.g., HumanoidBench), LLM RL (math reasoning with GRPO on Qwen2.5-Math-7B), and image classification (ResNet-50 on ImageNet). Below are actionable use cases, organized by deployment horizon.
Immediate Applications
- RL policy training plugin for continuous control (replacing/augmenting entropy bonuses)
- What: Drop-in activation for SAC/PPO/TD-MPC2/FastSAC to enforce a minimum entropy floor without α-temperature scheduling; simplifies objectives and improves performance (>30% on HumanoidBench).
- Sectors: Robotics, industrial automation, logistics, energy/HVAC control, autonomous systems simulation.
- Tools/products/workflows: PyTorch/TensorFlow layer “ERA-Gaussian” for bounded actions; wrappers for SAC/TD-MPC2; ROS-compatible training nodes; MLOps dashboards with entropy-floor monitoring alerts.
- Assumptions/dependencies: Bounded action space (e.g., tanh or clipped Gaussian), diagonal covariance; target entropy selection or auto-compensation δ; training-time access to policy outputs; safety constraints handled separately.
- LLM RLHF/RLAIF training stabilizer for reasoning models
- What: ERA for on-policy GRPO/PPO to prevent entropy collapse during RL tuning, yielding large reasoning gains (e.g., +37.4% on AIME’25 for Qwen2.5-Math-7B); preserves sampling policy while adjusting update policy.
- Sectors: Software (AI assistants, coding/math copilots), education (tutoring), enterprise knowledge workers, research labs.
- Tools/products/workflows: Trainer plugin for TRL/Verl-style codebases; GRPO/PPO callback applying ERA to top-entropy tokens during updates; entropy-threshold policies (ωlow, ωhigh) and scaling k pre-configured.
- Assumptions/dependencies: On-policy RL setup; very large discrete action spaces; heuristic focusing on top ~20% high-entropy tokens; careful hyperparameters (k, ωlow, ωhigh); reward/advantage estimates remain valid.
- Vision classifier regularization to reduce overconfidence
- What: Softmax-ERA layer to enforce a per-sample minimum entropy, complementary to label smoothing and data augmentation; observed +0.69% top-1 on ImageNet with ResNet-50.
- Sectors: Healthcare imaging triage, manufacturing QC, retail product recognition, document classification, security vision.
- Tools/products/workflows: “ERA-Softmax” head for classification models in timm/Lightning; calibration-aware training pipelines; risk thresholds tied to entropy floor; model selection with comparable accuracy at lower overconfidence.
- Assumptions/dependencies: Proper entropy target (e.g., 0.6–1.2 in paper); works alongside label smoothing/mixup; monitor for too-high floors that might hurt precision.
- Robust exploration for offline-to-online RL (OBAC and similar)
- What: Ensure sufficient policy stochasticity when fine-tuning from offline datasets, reducing premature convergence and improving sample efficiency.
- Sectors: Industrial process control, operations research, recommender policy sim-fine-tuning.
- Tools/products/workflows: ERA module integrated with OBAC implementations; entropy-floor scheduling over fine-tuning epochs.
- Assumptions/dependencies: Offline dataset quality; bounded actions; proper δ compensation if using squashing.
- Hyperparameter simplification for entropy-regularized RL
- What: Eliminate α-temperature tuning and unstable entropy-bonus gradients in SAC-like methods; focus on reward optimization while maintaining exploration via activation.
- Sectors: Any RL deployment where tuning cost/time is high.
- Tools/products/workflows: Standardized ERA configs by task family; CI pipelines that validate entropy floors during training.
- Assumptions/dependencies: Reasonable default entropy targets or auto-tuning; stable σ range constraints.
- OOD robustness boosts for LLMs through controlled exploration
- What: Improved OOD performance on ARC-C, GPQA-Diamond, and MMLU-Pro via maintained entropy floor during RL training.
- Sectors: General-purpose assistants, research/analysis copilots, enterprise QA.
- Tools/products/workflows: Training recipes that apply ERA in early stages to avoid collapse; OOD evaluation harnesses to verify gains.
- Assumptions/dependencies: Transfer from math-domain RL signals to OOD tasks; reward design doesn’t unintentionally punish exploration.
- Model calibration and abstention systems
- What: Use ERA-induced entropy floors to support confidence-aware workflows (e.g., route low-confidence cases to human review).
- Sectors: Healthcare diagnostics triage, fintech risk alerts, legal document triage.
- Tools/products/workflows: Thresholding on entropy; fallbacks and human-in-the-loop protocols; dashboards tracking over-time calibration.
- Assumptions/dependencies: Entropy aligns with true uncertainty; domain-specific calibration still needed.
- Academic baselines and curriculum in exploration/entropy control
- What: Adopt ERA as a baseline for entropy-constrained optimization in courses and research, enabling cleaner ablations vs. loss-based bonuses.
- Sectors: Academia, research institutes.
- Tools/products/workflows: Public codebase; teaching notebooks demonstrating ERA vs. entropy bonuses across RL/Vision/LLM.
- Assumptions/dependencies: Students have access to standard deep learning stacks.
Long-Term Applications
- On-robot and real-world autonomous control with safer exploration
- What: Deploy ERA-enabled controllers to maintain measured exploration while respecting safety envelopes; reduce tuning and instability in high-DoF robots and drones.
- Sectors: Robotics, autonomous vehicles, warehousing, agriculture, inspection.
- Tools/products/workflows: ERA integrated with safety layers (CBFs/shielding); sim-to-real pipelines with adaptive entropy floors by phase.
- Assumptions/dependencies: Certified safety constraints beyond entropy; real-world disturbances; careful sim-to-real calibration.
- Clinical decision-support RL and calibrated diagnostics
- What: Encourage controlled exploration in policy-learning for treatment recommendations and maintain calibrated uncertainty in diagnostic classifiers.
- Sectors: Healthcare.
- Tools/products/workflows: ERA-enabled offline RL for treatment policy research; classifier heads with entropy floors plus abstention/referral pathways.
- Assumptions/dependencies: Regulatory approval; strong offline data; rigorous bias and safety audits; human oversight.
- Financial trading and bidding strategies with exploration governance
- What: Use ERA to avoid over-exploitation and regime overfitting in RL-based trading/ad-bidding; maintain exploration under non-stationarity.
- Sectors: Finance, ad-tech.
- Tools/products/workflows: ERA-tuned exploration schedules; risk overlays; backtesting across regimes; drift detection coupled to entropy targets.
- Assumptions/dependencies: Market impact and latency constraints; compliance; careful guardrails against exploratory losses.
- Energy and grid control optimization
- What: Control policies that preserve exploration while learning under uncertainty in demand/supply and equipment dynamics.
- Sectors: Energy, smart grids, building automation.
- Tools/products/workflows: ERA integrated into MPC/RL hybrids; adaptive entropy floors to reflect uncertainty; digital twins for validation.
- Assumptions/dependencies: Real-time reliability; regulatory compliance; robust simulation fidelity.
- Inference-time “entropy governor” for LLMs and generative models
- What: Adaptive temperature/penalty controller that targets response-level entropy ranges to balance creativity and reliability per task/user.
- Sectors: Consumer assistants, creative tools, code generation, customer support chatbots.
- Tools/products/workflows: Middleware that reads token-level entropies and adjusts temperature/top-p on-the-fly; task-aware entropy bands.
- Assumptions/dependencies: The paper’s LLM ERA variant targets training-time updates, not sampling; extending to inference requires additional validation to avoid semantic drift.
- Multi-agent systems and game-theoretic training
- What: Prevent premature convergence to brittle equilibria by maintaining entropy floors per agent; stabilize self-play curricula.
- Sectors: Robotics swarms, simulation, strategy games, market simulations.
- Tools/products/workflows: ERA per-agent activations; curriculum schedulers that modulate entropy bounds based on exploitability.
- Assumptions/dependencies: Complex dynamics and non-stationarity; careful joint tuning to avoid oscillations.
- Large-scale foundation model RL training at scale
- What: Systematize entropy floors in massive RL training runs (e.g., reasoning-focused models) to reduce collapse and improve OOD generalization.
- Sectors: Foundation model labs, cloud providers.
- Tools/products/workflows: Cluster-ready ERA modules; auto-tuning of δ/targets; monitoring for entropy compliance and reward-entropy conflicts.
- Assumptions/dependencies: Distributed training efficiency; compatibility with mixture-of-experts, memory replay, or group rollout designs.
- Active learning and data acquisition systems
- What: Use entropy floors to keep models sensitive to informative uncertainty regions, enhancing sample selection strategies over time.
- Sectors: Data-centric AI across vision/NLP/structured data.
- Tools/products/workflows: Active learning loops where ERA discourages overconfidence on underrepresented modes; acquisition functions layered on top of entropy signals.
- Assumptions/dependencies: Entropy correlates with annotation value; careful handling to avoid inflating uncertainty everywhere.
- Standards and policy around exploration and calibration reporting
- What: Encourage reporting entropy-target settings and compliance in model cards for systems using RL/uncertainty-aware classifiers.
- Sectors: Policy, governance, risk management.
- Tools/products/workflows: Documentation schemas including entropy floors, observed entropy trajectories, and calibration audits.
- Assumptions/dependencies: Community adoption; alignment with existing AI risk frameworks.
Notes on cross-cutting dependencies:
- Choosing entropy targets: While ERA reduces tuning vs. entropy bonuses, targets still matter; empirical ranges in the paper show robustness, but domain-specific sweeps or auto-tuning (δ) help.
- Architectural assumptions: Continuous control instantiation assumes diagonal Gaussian and bounded actions; discrete instantiation requires softmax logits access and invertible transform approximations.
- Interaction with existing regularizers: ERA complements label smoothing, data augmentation, and KL penalties, but very high floors can harm precision; monitor trade-offs.
- Compute/engineering: Overhead is modest (<7% in the paper), yet productionization requires library support, monitoring, and safety checks.
Glossary
- Activation layer: A neural network layer inserted to transform logits during training, here used to adjust entropy without changing the sampling policy. "we apply an activation layer to the logits to obtain a transformed set , defined as:"
- Activation function: A mapping applied to model outputs to enforce constraints; ERA uses it to regulate policy entropy. "We introduce an activation function , which transforms the initial parameters to a new set $z' = g(z)."</li> <li><strong>Advantage</strong>: A baseline-adjusted measure of action quality used to weight policy gradients. "The GRPO variant estimates the advantage $A(y)yK$ samples as:"</li> <li><strong>Actor-critic</strong>: An RL architecture that learns a policy (actor) and a value function (critic) concurrently. "SAC~\citep{haarnoja2018soft} is an off-policy actor-critic algorithm that updates a soft Q-function $Q_\phi\pi_\theta$."</li> <li><strong>Bellman residual</strong>: The error minimized when fitting the Q-function to the soft Bellman target in maximum-entropy RL. "The Q-function is updated by minimizing the soft Bellman residual $J_Q(\phi)$:"</li> <li><strong>Bounded hypercube</strong>: The constrained action space commonly used in continuous control, here $[-1, 1]^D$. "over the bounded hypercube $[-1, 1]^D$."</li> <li><strong>Clip-Cov</strong>: A recent entropy-control baseline for LLM RL that uses clipping with covariance-based regularization. "Notably, it outperforms strong entropy-based baselines such as KL-Cov and Clip-Cov by significant margins."</li> <li><strong>Clip-higher</strong>: A heuristic regularization technique for maintaining entropy in LLM training by clipping higher probabilities. "including clip-higher~\citep{yu2025dapo} and training exclusively on the high-entropy tokens"</li> <li><strong>Continuous control</strong>: RL tasks with continuous action spaces, often in robotics, where exploration/entropy control is critical. "for continuous control reinforcement learning agents, improving performance by more than 30\% over strong baselines such as SAC on the challenging HumanoidBench"</li> <li><strong>Entropy bonus</strong>: An additive term in the objective to encourage exploration via higher entropy. "these methods, which add an entropy bonus directly to the training objective, inevitably alter the optimization landscape"</li> <li><strong>Entropy collapse</strong>: A failure mode where policy entropy decays too low, reducing diversity and hurting performance. "Policy gradient methods~\citep{NIPS1999_464d828b} such as GRPO~\citep{shao2024deepseekmath} frequently suffer from entropy collapse~\citep{cui2025entropy}"</li> <li><strong>Entropy Regularizing Activation (ERA)</strong>: The proposed paradigm that enforces minimum entropy via output activations, decoupling the primary objective from entropy control. "We propose ERA, a new paradigm that constrains the sampling entropy above given thresholds by applying specially designed activations to the outputs of models."</li> <li><strong>Exponential moving average (EMA)</strong>: A smoothing update rule for target networks to stabilize training. "The target network parameters $\phi'\phi' \leftarrow \tau \phi + (1-\tau)\phi'$."</li> <li><strong>FastSAC</strong>: A faster variant of SAC used as a baseline in experiments. "HumanoidBench (8 tasks, with FastSAC)"</li> <li><strong>Forking tokens</strong>: High-entropy tokens in language generation that represent branching points critical to exploration. "these tokens are considered forking tokens, whose entropy is the target of regularization"</li> <li><strong>GRPO</strong>: A PPO-style on-policy RL method for LLMs that uses group-relative advantages. "The GRPO variant estimates the advantage $A(y)yK$ samples as:"</li> <li><strong>KL-Cov</strong>: An entropy-control baseline leveraging KL and covariance regularization in LLM RL. "Notably, it outperforms strong entropy-based baselines such as KL-Cov and Clip-Cov by significant margins."</li> <li><strong>Label smoothing</strong>: A classification regularization that softens targets to prevent overconfidence. "boosting performance on top of strong data augmentation and label smoothing~\citep{szegedy2016rethinking}"</li> <li><strong>Lagrangian dual</strong>: The dual optimization formulation used to handle entropy constraints in maximum-entropy RL. "Practical algorithms like Soft Actor-Critic (SAC)~\citep{haarnoja2018soft} solve the Lagrangian dual of this problem."</li> <li><strong>Maximum entropy reinforcement learning</strong>: An RL framework that maximizes reward subject to a minimum entropy constraint. "the maximum entropy RL framework aims to maximize the standard reward objective subject to a minimum entropy constraint $\mathcal{H}_0$:"</li> <li><strong>OBAC</strong>: An RL baseline algorithm used in experiments (Offline Behavior-regularized Actor-Critic). "including SAC, PPO, TD-MPC2 and OBAC."</li> <li><strong>Off-policy</strong>: Learning from data generated by a different behavior policy than the one being optimized. "SAC~\citep{haarnoja2018soft} is an off-policy actor-critic algorithm"</li> <li><strong>On-policy</strong>: Learning from data generated by the current policy being optimized. "are incompatible with the on-policy setting."</li> <li><strong>Out-of-distribution (OOD)</strong>: Data or benchmarks that differ from the training distribution, used to test generalization. "we evaluate ERA on three hard OOD benchmarks: ARC-C~\citep{clark2018think}, GPQA-Diamond~\citep{gpqa}, and MMLU-Pro~\citep{mmlu_pro}."</li> <li><strong>Pass@$k$</strong>: An evaluation metric that checks if any of k sampled solutions is correct. "The pass@$k$ results further indicate that ERA enhances exploration and strengthens the modelâs reasoning ability."</li> <li><strong>Policy entropy</strong>: The entropy of an action distribution, quantifying stochasticity and exploration. "Policy entropy, $\mathcal{H}(\pi(\cdot|s))$, measures the policy's stochasticity."</li> <li><strong>Policy gradient</strong>: A class of RL methods that optimize expected return via gradients of log probabilities weighted by advantage. "Policy gradient (PG) methods optimize $J(\pi_\theta) = \mathbb{E}_{\tau \sim \pi_\theta} \left[ \sum_{t=0}^{T} \gamma^t R(s_t, a_t) \right]$ via gradient ascent."</li> <li><strong>Proximal Policy Optimization (PPO)</strong>: A widely used on-policy RL algorithm employing a clipped surrogate objective. "For LLM~(LLM) alignment, Proximal Policy Optimization (PPO)~\citep{schulman2017proximal} is commonly used."</li> <li><strong>Q-function</strong>: The action-value function estimating expected return for a state-action pair. "SAC~\citep{haarnoja2018soft} is an off-policy actor-critic algorithm that updates a soft Q-function $Q_\phi$"</li> <li><strong>Reward shaping</strong>: Modifying the reward signal to guide learning, often adding entropy terms to balance exploration. "A prevalent approach is reward shaping~\citep{cheng2025reasoning}, which augments the reward or advantage with an entropy bonus"</li> <li><strong>Soft Actor-Critic (SAC)</strong>: An off-policy, maximum-entropy RL algorithm with a temperature parameter. "SAC~\citep{haarnoja2018soft} later employed a maximum-entropy objective with a dynamically adjusted temperature parameter, but this can lead to instability."</li> <li><strong>Softmax policy</strong>: A discrete action distribution produced by applying softmax to logits. "and the softmax policy prevalent in discrete spaces."</li> <li><strong>Squashed Gaussian policy</strong>: A Gaussian policy passed through a tanh to bound actions within a range. "A popular method is to use a squashed Gaussian policy, which outputs a bounded action $a = \tanh(u)$"</li> <li><strong>TD-MPC2</strong>: A model-predictive control-based RL baseline used for benchmarking. "(b) Continuous Control: ERA significantly improves multiple popular RL algorithms, including SAC, PPO, TD-MPC2 and OBAC."</li> <li><strong>Temperature parameter</strong>: A scalar in maximum-entropy objectives controlling entropy weighting (often denoted $\alpha$). "with a dynamically adjusted temperature parameter, but this can lead to instability."</li> <li><strong>Target network</strong>: A slowly updated network used to compute stable targets in value updates. "with a target Q-network $Q_{\phi'}$."</li> <li><strong>Truncated Gaussian distribution</strong>: A Gaussian restricted to fixed bounds to ensure actions lie within a valid range. "directly sample actions from a Truncated Gaussian distribution $\pi_\theta(\cdot|s)=\text{TN}(\mu_\theta(s), \Sigma_\theta(s), -1, 1)$"
Collections
Sign up for free to add this paper to one or more collections.
