Entropy-guided sequence weighting for efficient exploration in RL-based LLM fine-tuning (2503.22456v2)

Abstract: We introduce Entropy-Guided Sequence Weighting (EGSW), a novel approach that enhances the exploration-exploitation tradeoff by dynamically assigning weights to generated outputs based on their advantage and entropy for Reinforcement Learning-based LLM fine-tuning. EGSW integrates entropy regularization with advantage-based weighting to balance policy updates, enabling efficient exploration in high-dimensional state spaces. By employing temperature-scaled softmax weighting over sequences, EGSW prioritizing high-reward, high-uncertainty steps while maintaining training stability. Although originally developed to improve Group Relative Policy Optimization (GRPO) during LLM fine-tuning, EGSW is generalizable to other reinforcement learning (RL) algorithms and can be implemented in both step-wise and trajectory-wise settings. Empirical evaluations demonstrate that EGSW enhances GRPO reasoning ability, yielding improvements in sample efficiency. Future work will explore the application of EGSW to advanced RL methodologies.

• The paper introduces Entropy-Guided Sequence Weighting (EGSW) to dynamically balance exploration and exploitation in RL-based LLM fine-tuning.
• EGSW integrates entropy regularization with advantage-based weighting to boost reward scores and enhance reasoning capabilities in LLMs.
• Experiments on Qwen2.5-Math models highlight that precise hyperparameter tuning of α and P is crucial for achieving stable and improved performance.

Entropy-Guided Sequence Weighting for Efficient Exploration in RL-Based LLM Fine-Tuning

This paper introduces Entropy-Guided Sequence Weighting (EGSW), a novel method designed to enhance exploration during RL-based fine-tuning of LLMs. EGSW dynamically adjusts the weights of generated sequences based on both their advantage and entropy, effectively balancing exploration and exploitation. The method aims to improve reasoning capabilities in LLMs by prioritizing high-reward, high-uncertainty steps, and it is generalizable to both step-wise and trajectory-wise RL frameworks.

Background and Motivation

The primary challenge in fine-tuning LLMs with RL lies in efficiently exploring high-dimensional state spaces. Traditional methods like MCTS are computationally expensive, rendering them impractical for LLM fine-tuning. While search-free methods such as GRPO offer computational efficiency, they often suffer from suboptimal exploration due to their reliance on policy-driven sampling. EGSW addresses these limitations by integrating entropy regularization with advantage-based weighting, promoting a more balanced and efficient exploration strategy.

Entropy-Guided Sequence Weighting (EGSW)

EGSW enhances the exploration-exploitation tradeoff by dynamically assigning weights to generated sequences based on their advantage and entropy. The raw weight for sequence $t$ is computed as:

%%%%1%%%%

where $A_{i, t}$ is the advantage, $H_{i, t}$ is the entropy, $\alpha$ is a hyperparameter scaling the entropy contribution, and $P$ is a temperature parameter controlling weight distribution sparsity. The entropy at step $t$, $H_{i,t}$, is calculated as:

$$H_{i,t} = - \sum_{a \in \mathcal{A}} \pi_{\theta}(a | q, a_{i,<t}) \log \pi_{\theta}(a | q, a_{i,<t}),$$

where $\pi_{\theta}(a | q, a_{i,<t})$ is the probability of selecting action $a$ given state $q$ under policy $\pi_{\theta}$, and $\mathcal{A}$ represents the action space. These raw weights are then normalized using a softmax function to ensure proper scaling and training stability:

$$w_{i,t} = \frac{w_{i,t}^{\text{raw}}}{\sum_{j=1}^{N} w_{j,t}^{\text{raw}}} = \frac{\exp\left(\frac{A_{i,t} + \alpha H_{i,t}}{P}\right)}{\sum_{j=1}^{N} \exp\left(\frac{A_{j,t} + \alpha H_{j,t}}{P}\right)}.$$

The normalized weights $w_{i,t}$ are used to reweight the policy gradient update, given by:

$$\nabla_\theta \mathcal{J}_{\text{EGSW}}(\theta) = \frac{1}{K} \sum_{i=1}^{K} \frac{1}{N_{k}} \sum_{t=1}^{N_{k}} w_{i,t} \Bigg[ \hat{A}_{i,t} + \beta \left( \frac{\pi_{\text{ref}}(a_{i,t}|q, a_{i,<t})}{\pi_{\theta}(a_{i,t}|q, a_{i,<t})} - 1 \right) \Bigg] \nabla_\theta \log \pi_\theta(a_{i,t}|q, a_{i,<t}).$$

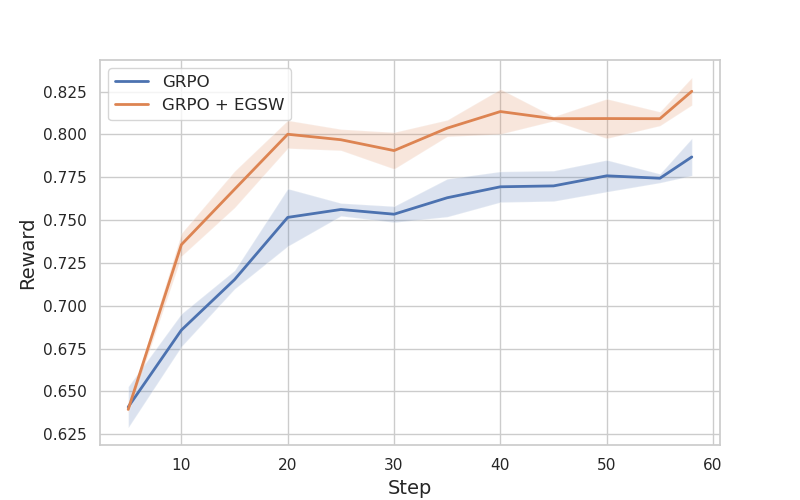
Figure 1: Training reward of the methods based on Qwen2.5-Math-7B.

Experimental Results

The authors fine-tuned EGSW on top of the GRPO framework, adopting the Simple-RL Reason approach with Qwen2.5-Math-7B and Qwen2.5-Math-7B-Instruct as base models. The integration was implemented using the Hugging Face open-r1, transformers, and trl repositories.

Experiments demonstrated that EGSW consistently outperformed standard GRPO in terms of reward scores. For hyperparameter tuning, the scaling coefficient $\alpha$ was adjusted between 0.15 and 0.50, and the temperature parameter $P$ was explored between 1 and 2. The optimal performance for Qwen2.5-Math-7B-Instruct was achieved with normalized entropy, $\alpha = 0.8$, and $P = 1.8$, while Qwen2.5-Math-7B performed best with normalized entropy, $\alpha = 0.3$, and $P = 1$.

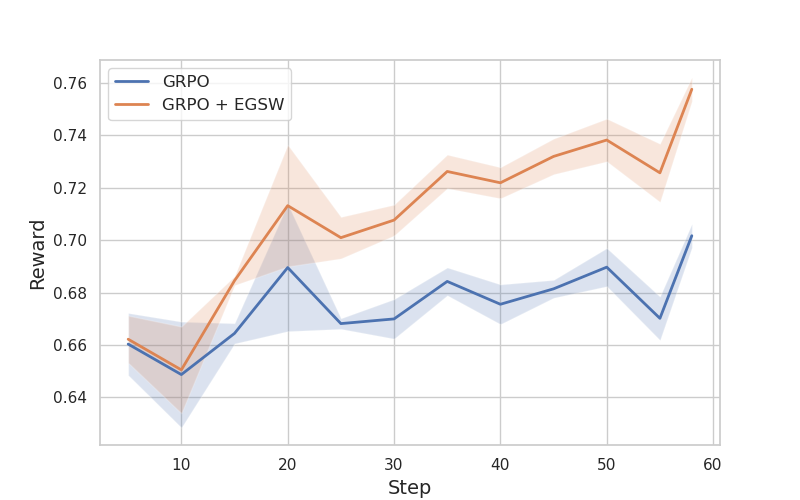
Figure 2: Training reward of the methods based on Qwen2.5-Math-7B-Instruct.

Discussion and Observations

A key observation is that fine-tuning Qwen2.5-Math-7B-Instruct with GRPO using an 8K MATH dataset alone did not improve the model’s reasoning capability, likely due to the model’s prior fine-tuning. However, incorporating EGSW enhanced the model’s reasoning ability, attributed to EGSW’s capacity to encourage better exploration. Moreover, the authors noted that effective exploration enables the model to generate fewer tokens while achieving higher rewards.

Figure 3: Completion length of the methods based on Qwen2.5-Math-7B.

The authors also highlight that EGSW is highly sensitive and requires careful hyperparameter tuning, particularly in balancing the entropy coefficient $\alpha$ to prevent excessive exploration. Additionally, EGSW reduces the overall gradient norm by using the weights, necessitating adjustments to the learning rate for stable learning.

Conclusion

The paper introduces EGSW as an effective method for enhancing the exploration-exploitation tradeoff in RL-based LLM fine-tuning. By integrating entropy into the weighting mechanism, EGSW promotes more diverse and informative trajectories while maintaining a focus on high-reward outputs. Empirical results demonstrate that EGSW enhances GRPO by achieving higher reward scores and improving reasoning capabilities. Future work could explore integrating EGSW with other reinforcement learning-based fine-tuning strategies to further enhance model performance across broader tasks.