The Unreasonable Effectiveness of Entropy Minimization in LLM Reasoning

Abstract: Entropy minimization (EM) trains the model to concentrate even more probability mass on its most confident outputs. We show that this simple objective alone, without any labeled data, can substantially improve LLMs' (LLMs) performance on challenging math, physics, and coding tasks. We explore three approaches: (1) EM-FT minimizes token-level entropy similarly to instruction finetuning, but on unlabeled outputs drawn from the model; (2) EM-RL: reinforcement learning with negative entropy as the only reward to maximize; (3) EM-INF: inference-time logit adjustment to reduce entropy without any training data or parameter updates. On Qwen-7B, EM-RL, without any labeled data, achieves comparable or better performance than strong RL baselines such as GRPO and RLOO that are trained on 60K labeled examples. Furthermore, EM-INF enables Qwen-32B to match or exceed the performance of proprietary models like GPT-4o, Claude 3 Opus, and Gemini 1.5 Pro on the challenging SciCode benchmark, while being 3x more efficient than self-consistency and sequential refinement. Our findings reveal that many pretrained LLMs possess previously underappreciated reasoning capabilities that can be effectively elicited through entropy minimization alone, without any labeled data or even any parameter updates.

• The paper introduces three novel EM approaches—EM-FT, EM-RL, and EM-INF—that enhance LLM reasoning without the need for labeled data.
• EM-FT reduces token-level entropy during finetuning, outperforming traditional methods on tasks like LeetCode and Minerva.
• EM-INF optimizes output logits at inference time, significantly improving performance on complex benchmarks such as SciCode.

The Unreasonable Effectiveness of Entropy Minimization in LLM Reasoning

This paper explores the application of entropy minimization (EM) techniques as a method to enhance reasoning capabilities of LLMs without relying on labeled data. The study introduces three novel approaches: EM-Finetuning (EM-FT), EM-Reinforcement Learning (EM-RL), and EM-Inference (EM-INF). It highlights how these methods can improve performance on tasks involving mathematical, physical, and coding challenges.

Entropy Minimization Techniques

EM-Finetuning (EM-FT)

EM-FT directly minimizes token-level entropy of unlabeled outputs during finetuning. This technique mirrors supervised finetuning by concentrating the model's output probability on the most likely tokens, thereby leveraging the latent knowledge inherent in pretrained models. EM-FT displays impressive results, outperforming conventional methods like GRPO and RLOO, particularly in tasks like LeetCode and Minerva.

EM-Reinforcement Learning (EM-RL)

EM-RL employs a negative entropy reward in reinforcement learning settings. Two variants, EM-RL-sequence and EM-RL-token, are based on minimizing trajectory-level and token-level entropy respectively. EM-RL achieves competitive performance against established RL methods despite not using any labeled data. In scenarios such as AMC and LeetCode, EM-RL consistently demonstrates robust improvements.

EM-Inference (EM-INF)

EM-INF operates at inference time, optimizing output logits to reduce entropy without updating model parameters. By adjusting logits to make the model's predictions more deterministic, EM-INF significantly improves the performance of models like Qwen-2.5-32B, surpassing proprietary models on complex tasks such as the SciCode benchmark.

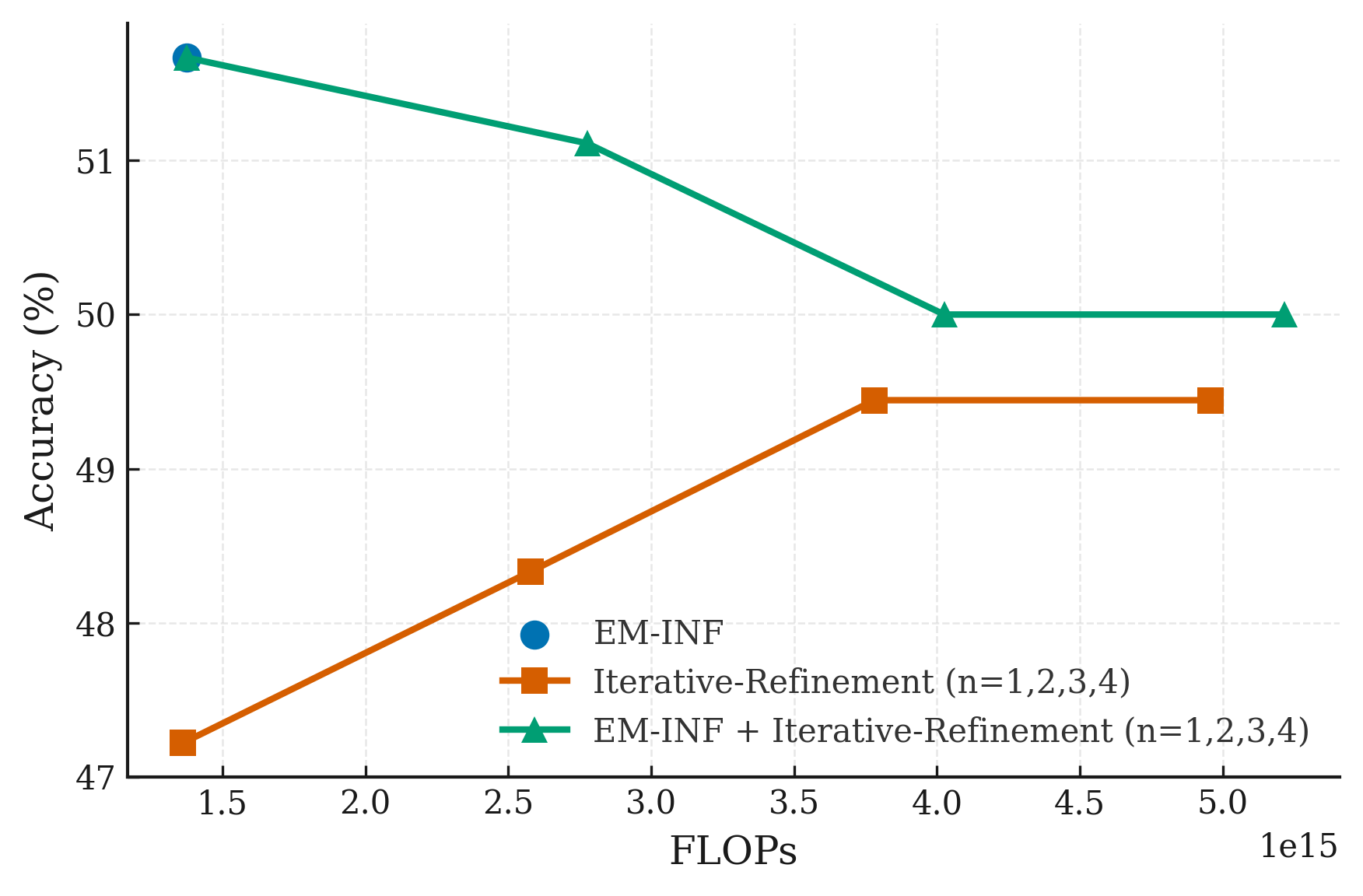
Figure 1: Accuracy vs. FLOPs for combining EM-INF and self-consistency at inference time on AMC.

Results and Analysis

The experimental results validate the effectiveness of entropy minimization as a standalone objective. Table comparisons indicate that EM-FT and EM-RL enhance model performance significantly across various reasoning tasks. EM-INF is particularly notable for its real-time applicability, functioning as an efficient inference scaling method for tackling high-uncertainty problems.

Figure 2: Qualitative analysis of EM-INF on SciCode. Qwen2.5-7B-Instruct's generated code (Left) fails to add random noise to all elements in the matrix, whereas the code generated with EM-INF (Right) performs the correct operation.

Limitations and Considerations

The success of these entropy minimization techniques is contingent on the underlying competency of the pretrained models. For models lacking inherent reasoning capabilities or when applied to tasks where confidence does not correlate with accuracy, EM may show limited efficacy. It may not enhance performance in value alignment tasks where model confidence is not a reliable quality indicator.

Conclusion

This research demonstrates that entropy minimization is an effective strategy for improving the reasoning capabilities of LLMs without labeled data or parameter updates. The experiments suggest that many pretrained models inherently possess strong reasoning abilities that can be enhanced through EM. Although EM is not universally applicable, it serves as a valuable baseline for future advancements in both post-training and inference-time scaling algorithms. The inclusion of EM in the evaluation of new methodologies could facilitate a more precise understanding of where improvements stem from and their implications for pretraining capabilities.