Learn to Guide Your Diffusion Model (2510.00815v1)

Abstract: Classifier-free guidance (CFG) is a widely used technique for improving the perceptual quality of samples from conditional diffusion models. It operates by linearly combining conditional and unconditional score estimates using a guidance weight $\omega$. While a large, static weight can markedly improve visual results, this often comes at the cost of poorer distributional alignment. In order to better approximate the target conditional distribution, we instead learn guidance weights $\omega_{c,(s,t)}$, which are continuous functions of the conditioning $c$, the time $t$ from which we denoise, and the time $s$ towards which we denoise. We achieve this by minimizing the distributional mismatch between noised samples from the true conditional distribution and samples from the guided diffusion process. We extend our framework to reward guided sampling, enabling the model to target distributions tilted by a reward function $R(x_0,c)$, defined on clean data and a conditioning $c$. We demonstrate the effectiveness of our methodology on low-dimensional toy examples and high-dimensional image settings, where we observe improvements in Fr\'echet inception distance (FID) for image generation. In text-to-image applications, we observe that employing a reward function given by the CLIP score leads to guidance weights that improve image-prompt alignment.

• The paper introduces a learnable guidance framework that adapts weights based on conditioning and denoising times, moving beyond fixed classifier-free guidance.
• It employs a self-consistency distributional objective to minimize discrepancies between forward diffusion and guided reverse processes, yielding improved FID and alignment.
• The approach extends to reward-guided generation for text-to-image tasks and demonstrates scalability across datasets like ImageNet and CelebA.

Learnable Conditional and Time-Dependent Guidance in Diffusion Models

Introduction

The paper "Learn to Guide Your Diffusion Model" (2510.00815) proposes a principled and empirically validated methodology for learning flexible, data- and condition-dependent guidance weights for conditional diffusion models. Motivated by the empirical observation that fixed classifier-free guidance (CFG) weights often do not optimally realign the model's output distribution with the target conditional, the authors generalize CFG by making the guidance weight a learnable function of the conditioning, as well as of the starting ($t$) and target ($s$) time steps in the denoising process. Notably, these weights are optimized via a distributional self-consistency objective that seeks to minimize the discrepancy (quantified by MMD or $\ell_2$-distance) between the forward diffusion and the guided reverse process, both conditionally and marginally.

This framework is also extended to reward-guided generation, enabling the use of arbitrary reward functions defined on the output and conditioning, with concrete instantiations for text-to-image alignment via CLIP score. The paper presents both rigorous probabilistic motivation and a thorough experimental suite, demonstrating improved Fréchet Inception Distance (FID) and prompt-alignment over constant-weight or manually-tuned guidance.

Methodological Advances

Generalization of Classifier-Free Guidance

Traditional CFG linearly interpolates denoiser outputs:

$$\hat{x}_\theta(x_t, c; \omega) = \hat{x}_\theta(x_t, c) + \omega \left[\hat{x}_\theta(x_t, c) - \hat{x}_\theta(x_t, \varnothing)\right]$$

where $\omega$ is a fixed scalar. However, it's known that high $\omega$ amplifies perceptual quality while moving samples off the support of $p(x_0 \mid c)$. The proposed framework replaces $\omega$ with $\omega^\phi_{c,(s,t)} = \omega(s, t, c;\phi)$, a neural network parameterized by $\phi$, allowing guidance strength to adapt to both the time interval of denoising and the conditioning.

The network outputs are ensured to be non-negative via a terminal ReLU. Training is performed post hoc on frozen denoisers, which is critical for compatibility with existing pretrained models.

Self-Consistency Distributional Objective

Rather than directly minimizing the (high-variance) marginal $MMD$ between guided and target conditional distributions, the authors employ a self-consistency objective:

$$p_{s|0,c}^{t,(\theta, \phi)}(x_s | x_0, c) \approx p_{s|0}(x_s|x_0)$$

where

$$p_{s|0,c}^{t,(\theta, \phi)}(x_s|x_0, c) = \int p_{s|t,0}(x_s|x_t, \hat{x}_\theta(x_t, c; \omega^\phi_{c,(s, t)})) p_{t|0}(x_t|x_0) dx_t$$

Minimizing the MMD or $\ell_2$-distance between samples from the true diffusion (forward) process and the guided reverse process, conditioned on $(x_0, c)$, provides a practical, low-variance learning signal for $\phi$.

The choice of time pairs $(s, t)$ is critical; the paper demonstrates superior performance when sampling $s$ and $t - s$ over larger intervals during training, relative to the small step sizes used at inference. This is empirically substantiated through detailed ablations.

Reward-based Guidance Extension

The method is further extended for reward-guided generation by incorporating a regularized reward-maximization loss:

$$L_{\text{tot}}(\phi) = \hat{\mathcal{L}}_{\beta,\lambda}(\phi) + \gamma_{R} L_{R}(\phi)$$

where $$L_{R}(\phi) = -\mathbb{E}[R(\hat{x}_{\theta}(x_t, c; \omega^\phi_{c,(s, t)}), c)]$$, and $\hat{\mathcal{L}}_{\beta,\lambda}$ is a self-consistency regularizer. This is crucial to avoid reward hacking and ensure that the guided process remains close to the target distribution.

Empirical Results and Analysis

ImageNet and CelebA

On ImageNet 64x64 and CelebA, learned guidance weights consistently outperform constant-weight baselines and carefully tuned limited-interval guidance schemes, with the strongest results seen when conditioning information is supplied to the guidance network.

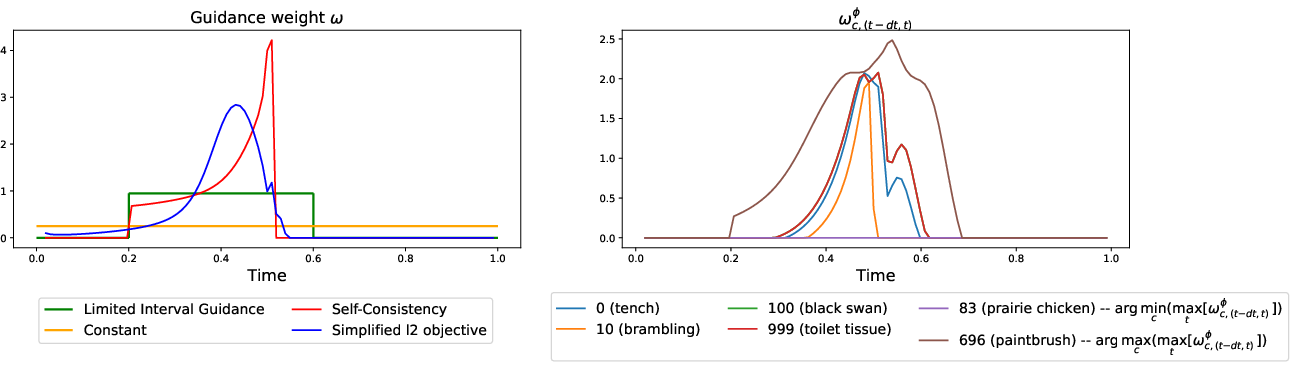
Figure 1: Learned guidance weights $\omega^\phi_{(t-\delta t, t)}$ for ImageNet 64x64 (left: conditioning-agnostic; right: class-specific).

A key finding is that the optimal guidance weight profile is non-constant, non-monotonic, and differs significantly between conditionings (see Figure 1). For some classes, the learned guidance is identically zero, while for others a large, sharply localized guidance is learned, highlighting the inadequacy of universal schedules.

Sensitivity to Training Hyperparameters

An extensive ablation (Figure 2) reveals that training with larger $\delta = t - s$ intervals during optimization (relative to those used at inference) yields guidance weights that generalize well, granting lower FID at test-time. The method exhibits some sensitivity to this parameter, especially under the $\ell_2$ variant, justifying careful selection.

Figure 2: Ablation: effect of $\delta$ and $S_{\min}$ on FID for ImageNet 64x64, across methods.

Text-to-Image Guidance with Reward

On MS-COCO 512x512 with text prompts, learned guidance weights outperform both unguided and fixed-weight baselines in FID, and—when coupled with CLIP score as reward—improve prompt-image alignment as evaluated by CLIP score. Importantly, guidance weights are prompt-dependent and can exhibit significant scale variation.

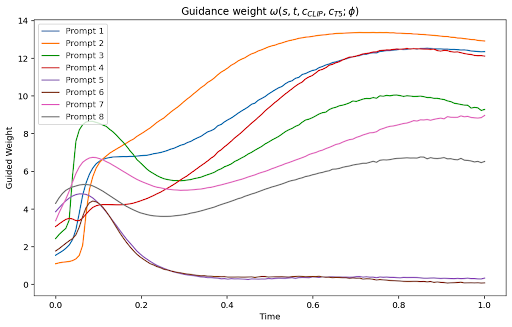
Figure 3: Learned prompt- and time-dependent guidance weights for text-to-image generation on COCO, using CLIP-score reward.

Sample generations (Figures 4-7) qualitatively validate that learned guidance delivers more realistic and better-aligned samples with the conditioning prompt compared to static guidance.

Figure 4: Man performing stunt on a skateboard on a road.

Figure 5: A light brown horse's face is shown at close range.

Figure 6: A small cutting board and knife with a cut apple.

Figure 7: Two birds sit on top of a parked car.

Low-Dimensional Diagnostics

In 2D Mixture of Gaussians benchmarks, the learned guidance network compensates for under-trained denoisers and can recover the target distribution more faithfully than static guidance—contradicting the theoretical CFG intuition that $\omega = 0$ is always best.

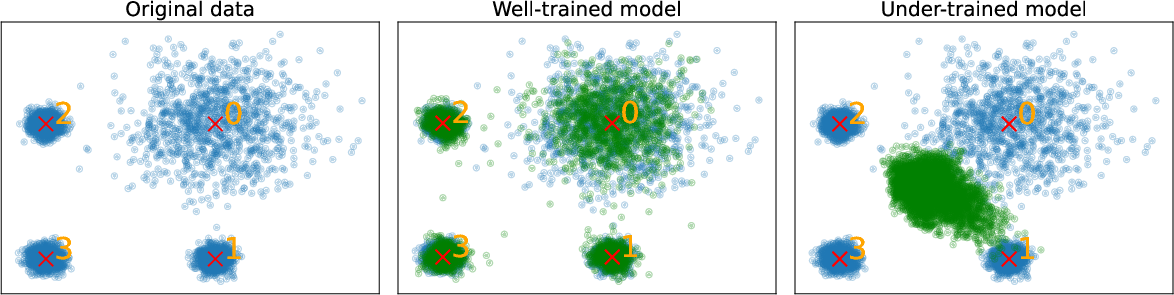
Figure 8: 2D MoG data and model samples, illustrating realignment by guided diffusion.

Guidance weights are high when the base model is under-trained, and zero when it is well-trained, confirming that learned guidance can compensate for mismatched denoisers rather than simply amplifying conditioning.

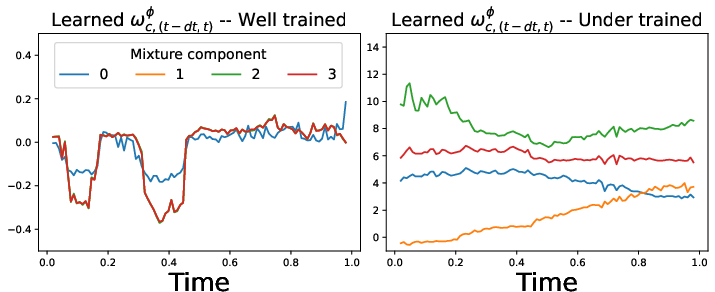
Figure 9: MMD between data and model samples as a function of guidance weight. Learned weights outperform both unguided and overamplified fixed guidance.

Figure 10: 2D MoG samples: blue (data), green (unguided), purple (learned guidance).

Positioning, Extensions, and Limitations

This framework is compatible with any conditional denoiser, and is agnostic to the backbone architecture, loss, or sampling method. The approach is orthogonal to SMC/MCMC-based correction schemes and can in principle be combined with them. It addresses prior theoretical objections to static CFG, and generalizes previous dynamic or heuristic weight scheduling methods by providing a data- and task-driven, distributional learning criterion.

One limitation is the increased complexity in real-time inference due to the need to evaluate a condition- and time-dependent network, although the cost is negligible relative to modern denoisers. Memory and compute scale linearly with the number of particle samples and batch size during guidance learning. The robustness to extreme prompt drift, as well as to out-of-distribution conditioning, is not extensively analyzed and may present failure modes.

Future Directions

Potential future work involves:

• Theoretical characterization of self-consistency solutions and generalization bounds in the overparameterized guidance regime.
• Extension to SDE- and ODE-based generative backbones, discrete diffusion, and other generative flows.
• Integration with active learning methods for reward functions, or adversarial adjustment to further minimize distributional shift.
• Deployment in reinforcement learning or model-based control, leveraging data-dependent time-scheduled guidance.

Conclusion

The paper systematically demonstrates that learnable, adaptive guidance weights enable conditional diffusion models to better approximate their target distributions, significantly surpassing static or heuristically scheduled guidance at both sample and distributional levels. The adaptive method accommodates complex dependencies on condition and denoising trajectory, leading to improved fidelity and alignment without the computational burden of particle-based corrections. This regime interprets CFG not merely as conditional mode-pushing, but as an implicit error correction parameter for approximate denoisers, and points to a new domain of optimization for diffusion guidance and control.