Inference-Time Alignment Control for Diffusion Models with Reinforcement Learning Guidance (2508.21016v1)

Abstract: Denoising-based generative models, particularly diffusion and flow matching algorithms, have achieved remarkable success. However, aligning their output distributions with complex downstream objectives, such as human preferences, compositional accuracy, or data compressibility, remains challenging. While reinforcement learning (RL) fine-tuning methods, inspired by advances in RL from human feedback (RLHF) for LLMs, have been adapted to these generative frameworks, current RL approaches are suboptimal for diffusion models and offer limited flexibility in controlling alignment strength after fine-tuning. In this work, we reinterpret RL fine-tuning for diffusion models through the lens of stochastic differential equations and implicit reward conditioning. We introduce Reinforcement Learning Guidance (RLG), an inference-time method that adapts Classifier-Free Guidance (CFG) by combining the outputs of the base and RL fine-tuned models via a geometric average. Our theoretical analysis shows that RLG's guidance scale is mathematically equivalent to adjusting the KL-regularization coefficient in standard RL objectives, enabling dynamic control over the alignment-quality trade-off without further training. Extensive experiments demonstrate that RLG consistently improves the performance of RL fine-tuned models across various architectures, RL algorithms, and downstream tasks, including human preferences, compositional control, compressibility, and text rendering. Furthermore, RLG supports both interpolation and extrapolation, thereby offering unprecedented flexibility in controlling generative alignment. Our approach provides a practical and theoretically sound solution for enhancing and controlling diffusion model alignment at inference. The source code for RLG is publicly available at the Github: https://github.com/jinluo12345/Reinforcement-learning-guidance.

• The paper introduces Reinforcement Learning Guidance (RLG), enabling dynamic inference-time control over alignment in diffusion models without additional training.
• It leverages a modified Classifier-Free Guidance mechanism to blend base and RL-finetuned outputs, allowing both interpolation and extrapolation of alignment strength.
• Empirical results in tasks like human preference alignment and text rendering demonstrate RLG’s effectiveness in enhancing generation fidelity and control.

Inference-Time Alignment Control for Diffusion Models with Reinforcement Learning Guidance

Introduction and Motivation

Diffusion and flow matching models have become the dominant paradigm for high-fidelity generative modeling, yet aligning their outputs with complex, downstream objectives—such as human preferences, compositional accuracy, or compressibility—remains a persistent challenge. While RL-based fine-tuning methods, inspired by RLHF for LLMs, have been adapted to these models, they suffer from two key limitations: (1) the intractability of exact sample likelihoods in diffusion models, which undermines the effectiveness of RL algorithms, and (2) the inflexibility of alignment strength, which is fixed post-fine-tuning and sensitive to hyperparameter choices (notably the KL regularization coefficient). This work introduces Reinforcement Learning Guidance (RLG), an inference-time method that enables dynamic, post-hoc control over the alignment-quality trade-off in diffusion models, without further training.

Theoretical Foundations of RLG

RLG is motivated by a reinterpretation of RL fine-tuning for diffusion models as implicit reward conditioning within the SDE framework. The key insight is that the RL-finetuned model can be viewed as sampling from a distribution proportional to the base model, exponentially weighted by the reward, i.e., $$p^*(\mathbf{x}) \propto p_{\text{ref}}(\mathbf{x}) \exp(\frac{1}{\beta} R(\mathbf{x}))$$. RLG adapts the Classifier-Free Guidance (CFG) mechanism by linearly interpolating the outputs (score or velocity fields) of the base and RL-finetuned models with a user-controlled scale $w$:

$$\hat{\mathbf{s}}_{\text{RLG}}(\mathbf{x}_t, t) = (1-w)\mathbf{s}_{\text{ref}}(\mathbf{x}_t, t) + w\mathbf{s}_{\theta}(\mathbf{x}_t, t)$$

This is mathematically equivalent to adjusting the effective KL-regularization coefficient in the RL objective to $\beta/w$, thus providing a principled mechanism for both interpolation ($w<1$) and extrapolation ($w>1$) of alignment strength at inference.

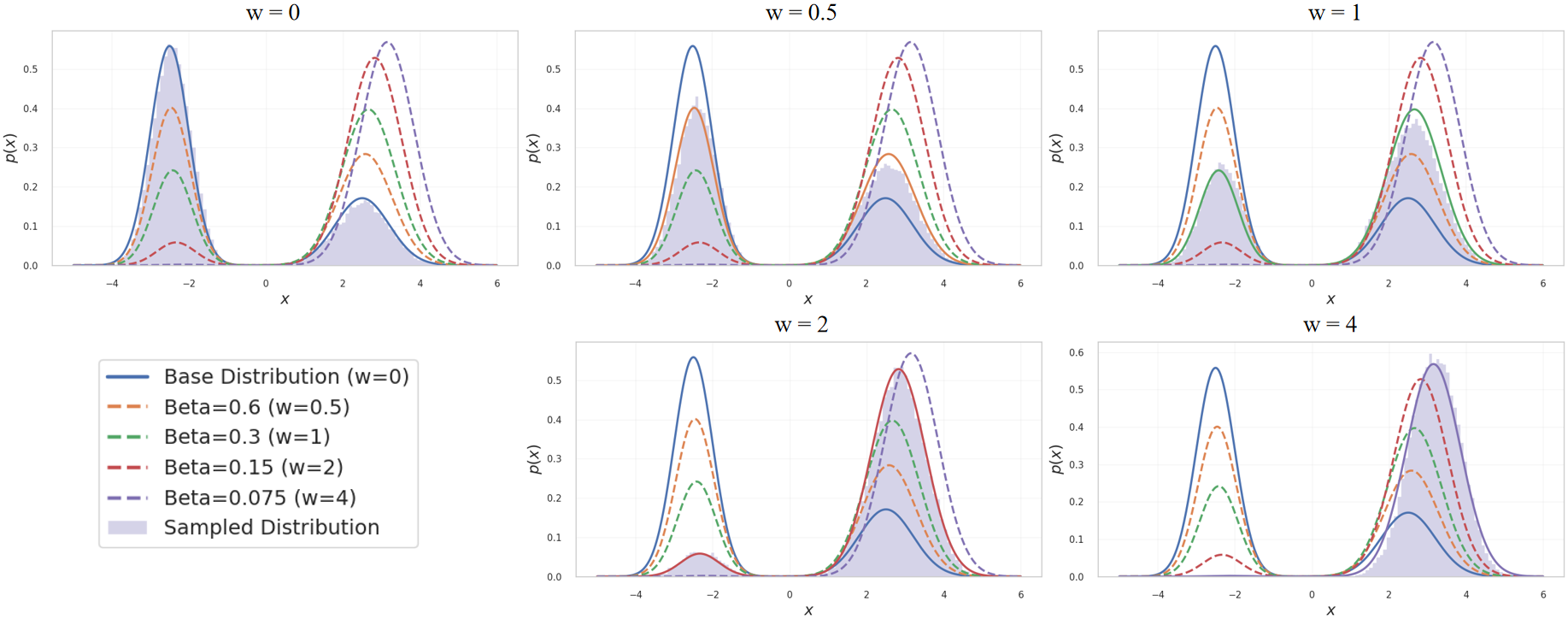
Figure 1: Small-scale demonstration supporting the theoretical justification of RLG. Each subplot shows the sampled distribution under a different RLG weight $w$, while the curves represent the corresponding theoretically predicted RL-fine-tuned distributions. Here, $\beta$ denotes the KL regularization coefficient.

Empirical validation in a controlled 1D flow matching setting confirms that varying $w$ in RLG produces output distributions that closely match those of RL-finetuned models with different KL coefficients, substantiating the theoretical equivalence.

Implementation and Practical Considerations

RLG is implemented as a simple modification to the sampling loop of diffusion or flow matching models. At each denoising step, the velocity (or score) is computed for both the base and RL-finetuned models, and a weighted sum is used to update the sample. The method is agnostic to the underlying RL algorithm (e.g., DPO, GRPO, SPO) and generative architecture (diffusion or flow matching), requiring only access to the two model checkpoints.

def rlg_sampling(x_init, v_ref, v_rl, w, num_steps, solver_step): x = x_init for t in range(num_steps): v_ref_t = v_ref(x, t) v_rl_t = v_rl(x, t) v_guided = (1 - w) * v_ref_t + w * v_rl_t x = solver_step(x, v_guided, t) return x

Resource requirements are minimal: RLG incurs only a 2x compute overhead per sampling step (due to dual model evaluation), with no additional training or memory cost. The method is compatible with all standard diffusion/flow pipelines and can be integrated into existing inference frameworks.

Empirical Results

Human Preference Alignment

RLG consistently improves the performance of RL-finetuned models across multiple architectures and RL algorithms. On the human preference alignment task, increasing the RLG scale $w$ leads to higher PickScores and more aesthetically pleasing images, as confirmed by automated reward models and qualitative inspection.

Figure 2: Selected qualitative results for the human preference alignment task using SD3.5-M with GRPO and RLG. As the RLG scale increases, images become more detailed and aesthetically pleasing, corroborated by rising PickScores.

Figure 3: Selected qualitative results for the human preference task. Images are generated from SD3.5 trained with GRPO, with different RLG scales.

Figure 4: Selected qualitative results for the human preference task. Images are generated from SD1.5 trained with DPO, with different RLG scales.

Figure 5: Selected qualitative results for the human preference task. Images are generated from SDXL trained with SPO, with different RLG scales.

Structured and Fidelity-Driven Generation

RLG demonstrates strong gains in tasks requiring compositional control (GenEval), text rendering (OCR), and fidelity (inpainting, personalization). For example, on the OCR task, increasing $w$ enables the model to render text with higher accuracy, surpassing the RL-finetuned baseline.

Figure 6: Selected qualitative results for the visual text rendering task. RLG with higher guidance scale ($w>1.0$) enables correct text rendering without loss in image quality.

Low-Level Property Control

RLG enables dynamic control over non-semantic properties such as image compressibility. By varying $w$, users can interpolate or extrapolate the degree of compressibility beyond what is achievable with static RL fine-tuning.

Figure 7: Selected qualitative results for the image compressibility task.

Figure 8: Selected qualitative results for the image compressibility task.

Compositional and Inpainting Tasks

RLG enhances compositional accuracy and inpainting quality, as evidenced by improved object arrangement and higher preference rewards.

Figure 9: Selected qualitative results for the compositional image generation task.

Figure 10: Selected qualitative results for the image inpainting task.

Trade-offs, Limitations, and Future Directions

RLG provides a flexible, inference-time mechanism for controlling the alignment-quality trade-off, overcoming the rigidity of static RL fine-tuning. However, it inherits certain limitations from CFG: the guided score does not guarantee sampling from the true target distribution, and the theoretical equivalence to KL-coefficient adjustment assumes convergence to the optimal RL policy, which may not hold for all RL algorithms (e.g., GRPO). Additionally, RLG requires both the base and RL-finetuned models to be available at inference.

Potential future directions include adaptive, timestep-dependent RLG scales, integration with other control methods, and further theoretical analysis of RLG under non-idealized RL objectives.

Conclusion

Reinforcement Learning Guidance (RLG) offers a theoretically principled, training-free approach for dynamic, inference-time control of alignment in diffusion and flow matching models. By interpolating between base and RL-finetuned models, RLG enables users to flexibly balance alignment and generation quality, supports both interpolation and extrapolation, and consistently enhances performance across a wide range of tasks and architectures. This work establishes RLG as a practical and generalizable tool for post-hoc alignment control in generative modeling.