Socratic-Zero : Bootstrapping Reasoning via Data-Free Agent Co-evolution (2509.24726v1)

Abstract: Recent breakthroughs in LLMs on reasoning tasks rely heavily on massive, high-quality datasets-typically human-annotated and thus difficult to scale. While data synthesis or distillation offers a promising alternative, existing methods struggle with inconsistent data quality and an inability to dynamically adapt to the evolving capabilities of the model, leading to suboptimal training signals. To address these limitations, we introduce Socratic-Zero, a fully autonomous framework that generates high-quality training data from minimal seed examples through the co-evolution of three agents: the Teacher, the Solver, and the Generator. The Solver continuously refines its reasoning by learning from preference feedback on both successful and failed trajectories; the Teacher adaptively crafts increasingly challenging questions based on the Solver's weaknesses; and the Generator distills the Teacher's question-design strategy to enable scalable, high-fidelity curriculum generation. This closed-loop system produces a self-improving curriculum-requiring no pre-existing tasks or labels. Remarkably, starting from only 100 seed questions, our Socratic-Solver-8B achieves an average gain of +20.2 percentage points over prior data synthesis methods across seven mathematical reasoning benchmarks (AMC23, AIME24-25, Olympiad, MATH-500, Minerva, and GSM8K), with consistent gains on both Qwen3 and GLM4 series models. Even more surprisingly, synthetic data from Socratic-Generator-32B enables student LLMs to achieve superior performance compared to other state-of-the-art (SOTA) commercial LLMs on these benchmarks, including Qwen3-235B-A22B, DeepSeek-V3.1-671B, GPT-5, Gemini-2.5-Pro, Grok-4, and Claude-4.1-Opus.

• The paper introduces a novel autonomous framework where Teacher, Solver, and Generator co-evolve to bootstrap mathematical reasoning in LLMs.
• The methodology employs Direct Preference Optimization for the Solver and value-weighted supervised fine-tuning for the Generator, achieving a +20.2 point gain over baselines.
• Empirical results demonstrate scalable curriculum evolution with robust cross-architecture generalization and superior synthetic data quality.

Socratic-Zero: A Co-evolutionary, Data-Free Framework for Bootstrapping Reasoning in LLMs

Introduction

Socratic-Zero introduces a fully autonomous, multi-agent co-evolutionary framework for bootstrapping mathematical reasoning in LLMs from minimal seed data, entirely eliminating the need for large-scale, human-annotated datasets. The framework operationalizes a Socratic learning paradigm, where three agents—Teacher, Solver, and Generator—interact in a closed loop to generate, solve, and refine mathematical problems. This approach addresses the scalability and adaptability limitations of prior data synthesis and distillation methods, which typically rely on static datasets and lack dynamic curriculum adaptation.

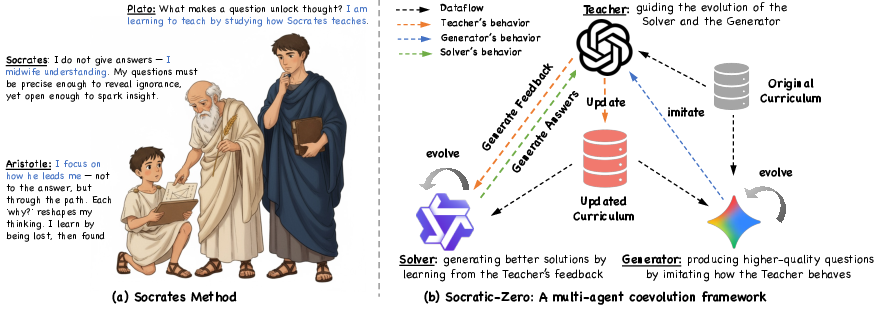
Figure 1: The Socratic-Zero framework, inspired by the Socratic method, operationalizes a co-evolutionary system where a Teacher LLM guides the Solver and Generator agents through iterative feedback and curriculum evolution.

Framework Architecture and Methodology

Multi-Agent Co-evolution

The Socratic-Zero framework consists of three core agents:

• Teacher: A high-capacity, frozen LLM that provides deterministic oracle functions for solution verification and problem refinement.
• Solver: A trainable LLM that attempts to solve problems and improves via preference-based learning from the Teacher's feedback.
• Generator: A trainable LLM that distills the Teacher's problem generation strategy, producing new problems that are optimally challenging for the Solver.

The system operates in iterative cycles. At each iteration, the Solver attempts to solve a curriculum of problems, the Teacher identifies and analyzes failures, and the Generator learns to mimic the Teacher's refinement strategy. The curriculum is dynamically expanded with new problems targeting the Solver's weaknesses, ensuring that the training signal remains maximally informative and adaptively challenging.

Figure 3: The co-evolutionary loop: (a) Solver evolves via DPO on preference pairs, guided by the Teacher's verification and problem generation; (b) Generator distills the Teacher's strategy using value-weighted supervised learning, enabling scalable curriculum generation.

Solver Training: Direct Preference Optimization

The Solver is updated using Direct Preference Optimization (DPO), leveraging preference pairs constructed from correct and incorrect solution attempts as judged by the Teacher. For each problem, the Solver generates multiple solution trajectories, which are partitioned into "winning" (correct) and "losing" (incorrect) sets. The DPO loss encourages the Solver to increase the likelihood of preferred (winning) solutions relative to rejected (losing) ones, using a frozen reference policy for regularization. This approach provides a stable and efficient alternative to RLHF, directly optimizing for solution quality without reward model training.

Generator Training: Value-Weighted Supervised Fine-Tuning

The Generator is trained to distill the Teacher's problem refinement strategy via weighted supervised fine-tuning (WSFT). A utility function, modeled as a Gaussian centered at a target Solver success rate (typically $\mu=0.5$), scores each generated problem based on its informativeness—problems that are neither too easy nor too hard are preferred. The Generator's objective is to maximize the utility-weighted log-likelihood of producing the Teacher's refined problems, internalizing expert curriculum design principles and enabling scalable, high-fidelity synthetic data generation.

Curriculum Evolution and Quality Control

The curriculum is expanded at each iteration by incorporating new problem-solution pairs generated from Solver failures. Problems are dynamically categorized into "mastered," "learning," and "too difficult" zones based on Solver performance, ensuring that curriculum expansion remains within the Solver's zone of proximal development. Rigorous quality control mechanisms, including dual-verification (rule-based and LLM-based) and Teacher self-verification, prevent the propagation of erroneous or ambiguous problems.

Empirical Results

Solver Performance

Socratic-Zero demonstrates substantial improvements over strong baselines (Static Augmentation, LLM2LLM) across seven mathematical reasoning benchmarks (AMC, Minerva, MATH-500, GSM8K, Olympiad, AIME-24, AIME-25). The Socratic-Solver-8B achieves an average accuracy of 56.1%, representing a +20.2 point gain over the best baseline. Notably, the framework exhibits robust cross-architecture generalization, with similar gains observed on GLM4-9B and Qwen3-14B models. Improvements in mathematical reasoning also transfer to general cognitive benchmarks (BBEH, MMLU-Pro, SuperGPQA), with an average gain of +6.02 points.

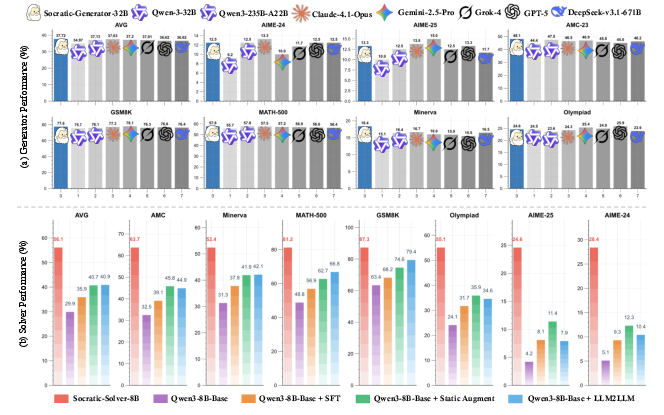
Figure 2: (a) Socratic-Generator-32B enables student models to match or exceed much larger SOTA models; (b) Socratic-Solver-8B achieves a +20.2 point improvement over the baseline.

Generator Effectiveness

The Socratic-Generator-32B achieves a 95.6% validity rate for generated problems, rivaling or surpassing much larger commercial models (e.g., GPT-5, Gemini-2.5-Pro, Claude-4.1-Opus). Downstream, student models fine-tuned on Socratic-Generator-32B data achieve 37.72% average accuracy, outperforming those trained on data from larger models, including its own Teacher (Qwen3-235B-A22B). This result demonstrates that strategic specialization and curriculum adaptation can yield superior training signals compared to brute-force parameter scaling.

Ablation Studies

Ablation experiments confirm the necessity of initial supervised fine-tuning (SFT) for effective RL-based curriculum learning; models without SFT show minimal improvement. The Gaussian utility function with $\mu=0.5$ and $\sigma=0.2$ is empirically optimal for Generator training, with alternative reward formulations yielding consistently lower performance.

Implementation Considerations

Computational Requirements

• Solver/Generator Training: Conducted on 8×NVIDIA H20 GPUs (96GB each) with mixed-precision training and gradient checkpointing.
• Teacher Inference: Deployed on 16×AMD MI308X GPUs (192GB each) for high-throughput curriculum generation and evaluation.
• Distributed Training: Utilized PyTorch DDP with NCCL backend for efficient multi-GPU synchronization.

Hyperparameters

• Solver SFT: LR=5e-5, batch size=2, LoRA rank=64, 1 epoch.
• Solver DPO: LR=1e-6–5e-6, batch size=2, DPO $\beta$=0.05–0.2.
• Generator WSFT: LR=1e-5, batch size=1, 2 epochs.
• Curriculum: $k=8$ solution attempts per problem, historical replay ratio=25%.

Deployment and Scaling

The modular architecture allows independent scaling of Solver, Teacher, and Generator components. The framework supports cross-architecture deployment and can be extended to multi-domain or hierarchical curriculum evolution. Quality control and curriculum stability mechanisms ensure robust performance as the system scales.

Theoretical and Practical Implications

Socratic-Zero provides empirical evidence for the viability of fully autonomous, data-free curriculum learning in LLMs. The co-evolutionary dynamics yield bounded oscillatory convergence, with the system reaching dynamic equilibria where curriculum difficulty and Solver capability are balanced. The framework's domain-agnostic value function and curriculum evolution mechanisms suggest potential for transfer to other reasoning domains (e.g., physics, computer science) with appropriate adaptation of Teacher evaluation capabilities.

The results challenge the prevailing paradigm of scaling LLMs primarily through data and parameter increases, demonstrating that strategic, adaptive curriculum generation can yield superior performance with significantly reduced resource requirements. The framework's extensibility and modularity position it as a foundation for future research in autonomous reasoning, scientific discovery, and complex system modeling.

Conclusion

Socratic-Zero establishes a new paradigm for autonomous reasoning improvement in LLMs, leveraging multi-agent co-evolution and adaptive curriculum learning to achieve state-of-the-art performance from minimal seed data. The framework's empirical success across diverse benchmarks, robust cross-architecture generalization, and superior synthetic data quality underscore the efficacy of co-evolutionary learning. Future work should focus on formal convergence analysis, domain transferability, and extension to broader reasoning tasks, with the goal of developing scalable, resource-efficient AI systems capable of continual self-improvement.