Absolute Zero: Reinforced Self-play Reasoning with Zero Data (2505.03335v2)

Abstract: Reinforcement learning with verifiable rewards (RLVR) has shown promise in enhancing the reasoning capabilities of LLMs by learning directly from outcome-based rewards. Recent RLVR works that operate under the zero setting avoid supervision in labeling the reasoning process, but still depend on manually curated collections of questions and answers for training. The scarcity of high-quality, human-produced examples raises concerns about the long-term scalability of relying on human supervision, a challenge already evident in the domain of LLM pretraining. Furthermore, in a hypothetical future where AI surpasses human intelligence, tasks provided by humans may offer limited learning potential for a superintelligent system. To address these concerns, we propose a new RLVR paradigm called Absolute Zero, in which a single model learns to propose tasks that maximize its own learning progress and improves reasoning by solving them, without relying on any external data. Under this paradigm, we introduce the Absolute Zero Reasoner (AZR), a system that self-evolves its training curriculum and reasoning ability by using a code executor to both validate proposed code reasoning tasks and verify answers, serving as an unified source of verifiable reward to guide open-ended yet grounded learning. Despite being trained entirely without external data, AZR achieves overall SOTA performance on coding and mathematical reasoning tasks, outperforming existing zero-setting models that rely on tens of thousands of in-domain human-curated examples. Furthermore, we demonstrate that AZR can be effectively applied across different model scales and is compatible with various model classes.

• The paper introduces the Absolute Zero paradigm, a self-play approach that trains reasoning models without human-curated data.
• The methodology employs a unified model as both proposer and solver, using code execution to validate and improve generated tasks.
• Experimental results demonstrate state-of-the-art performance on coding and mathematical reasoning tasks, with improvements scaling with model size.

Absolute Zero: Reinforced Self-play Reasoning with Zero Data

This paper introduces a novel RLVR paradigm called Absolute Zero, designed to train reasoning models without relying on any human-curated data (2505.03335). The approach involves a single model learning to propose tasks that maximize its own learning progress and improving reasoning by solving them, using a code executor to validate proposed code reasoning tasks and verify answers. The system, named Absolute Zero Reasoner (AZR), achieves SOTA performance on coding and mathematical reasoning tasks, outperforming existing zero-setting models trained on human-curated examples, demonstrating its applicability across different model scales and classes.

The Absolute Zero Paradigm

The paper addresses the limitations of existing RLVR methods, which depend on expertly curated datasets of question-answer pairs, raising concerns about scalability and potential constraints on AI's autonomous learning. To overcome these limitations, the Absolute Zero paradigm is introduced, where a model learns to define tasks that maximize learnability and solve them effectively through self-play, without external data.

Figure 1: The Absolute Zero paradigm contrasts with supervised learning and RLVR by eliminating the need for human-curated data and enabling self-improving task proposal and solution through self-play.

The Absolute Zero paradigm aims to shift the burden of data scaling from human experts to the $\pi_\theta^\text{propose}$ and the environment $e$, which are responsible for evolving the learning task distribution, validating proposed tasks, and providing grounded feedback. This approach allows for continuous improvement through self-play. The objective function for the Absolute Zero setting is defined as:

$\mathcal{J}(\theta)\coloneqq\max_{\theta}\;\; \mathbb{E}_{z \sim p(z)}\Bigg[ \; \mathbb{E}_{\textcolor{envgreen}{(x, y^\star) \sim f_e( \cdot | \tau), \tau\sim\pi_\theta^{\text{propose}( \cdot | z)}\bigg[ r^\text{propose}_{\textcolor{envgreen}{e}(\tau, \pi_\theta) + \lambda \, \mathbb{E}_{y \sim \pi_\theta^{\text{solve}(\cdot \mid x)}\big[ r^\text{solve}_{\textcolor{envgreen}{e}(y, y^\star) \big] \bigg] \Bigg].$

Absolute Zero Reasoner (AZR)

The paper presents AZR as an instantiation of the Absolute Zero paradigm, where a unified LLM acts as both a proposer and solver, generating tasks to evolve its learning curriculum and attempting to solve them to enhance reasoning capabilities. The model is trained jointly with both roles, learning to create tasks that push the boundary of reasoning capacity while improving its ability to solve them effectively.

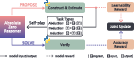
Figure 2: The Absolute Zero Reasoner proposes tasks, solves them, and updates its parameters using rewards from both stages.

AZR constructs three types of coding tasks, corresponding to abduction, deduction, and induction, using code as a verifiable medium for task construction and verification. The two roles are proposer and solver. The proposer generates tasks, and the solver attempts to solve them. The reward function for the proposer encourages the generation of tasks with meaningful learning potential, while the solver receives a binary reward based on the correctness of its final output. For the proposer, the reward is defined as:

$r_{\text{propose} = \begin{cases} 0, & \text{if } \bar{r}_{\text{solve} = 0 \text{ or } \bar{r}_{\text{solve} = 1 \ 1 - \bar{r}_{\text{solve}, & \text{otherwise}, \end{cases}$

AZR uses code executor as both a flexible interface and a verifiable environment. Given a program space $\mathscr{P}$, input space $\mathscr{I}$ and output space $\mathscr{O}$, an AZR reasoning task is defined as a triplet $(p, i, o)$, where $p \in \mathscr{P}$ is a program, $i \in \mathscr{I}$ is an input, and $o \in \mathscr{O}$ is the corresponding output produced by running program on input, $o=p(i)$. The core reasoning modes are:

• Deduction: predicting the output $o$ given a program $p$ and input $i$
• Abduction: inferring a plausible input $i$ given the program $p$ and an output $o$
• Induction: synthesizing a program $p$ from a set of in-out examples $\{(i^n, o^n)\}$

The paper discusses implementation details of the AZR self-play algorithm, including buffer initialization, buffer usage, construction of valid tasks, validating solutions, and advantage estimator calculation. AZR employs Task-Relative REINFORCE++ (TRR++) to compute separate baselines for each task-role configuration.

Experimental Results

The experimental setup involves training AZR models on Qwen2.5-7B and Qwen2.5-7B-Coder, resulting in Absolute Zero Reasoner-base-7B and Absolute Zero Reasoner-Coder-7B, respectively. The models are evaluated on in-distribution and out-of-distribution datasets, with an emphasis on coding and mathematical reasoning benchmarks.

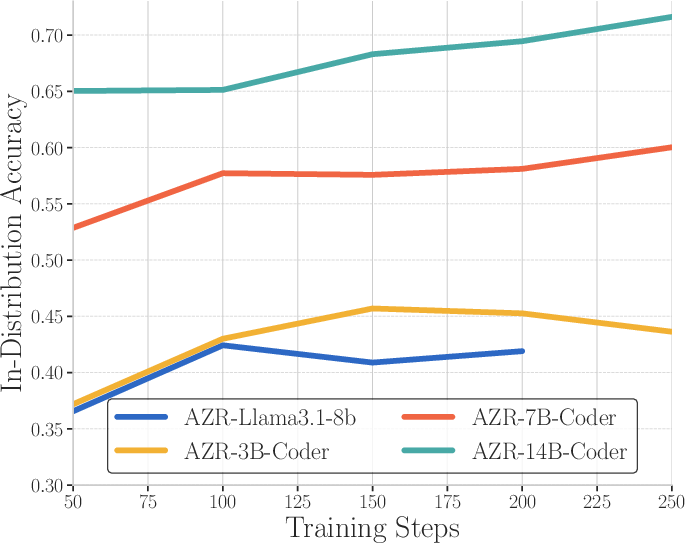
Figure 3: Comparison of in-distribution and out-of-distribution reasoning task performances across different model sizes and types.

The results demonstrate that AZR achieves state-of-the-art performance in both the 7B overall average and coding average categories, surpassing previous models trained with expert-curated human data in the coding category. The coder variant exhibited better performance in both math and coding after the AZR self-play process. Performance improvements scale with model size, suggesting continued scaling is advantageous for AZR. Interestingly, the trained models exhibit distinct reasoning patterns depending on the task type.

Related Work

The paper discusses related work in reasoning with RL and self-play, highlighting the limitations of existing approaches and positioning Absolute Zero as a novel paradigm for achieving superhuman reasoning capabilities. The self-play paradigm is a notable precursor to AZR and can be traced back to early 2000s two-agent systems in which a proposal agent invents questions for a prediction agent to answer. This dynamic continuously and automatically improves both agents, enabling theoretically never-ending progress.

Conclusion

The paper concludes by emphasizing the potential of the Absolute Zero paradigm to drive superior reasoning capabilities without extensive domain-specific training data. AZR demonstrates strong performance across diverse reasoning tasks and scales efficiently. Future research directions include exploring different environments for verifiable feedback, extending AZR to embodied AI, and designing exploration/diversity rewards for both propose and solve roles.

The paper highlights a limitation regarding the safe management of self-improving components, as evidenced by instances of safety-concerning CoT from the Llama-3.1-8B model. The exploration component of RL is recognized as a critical driver for emergent behavior, suggesting the benefit of dynamically defining and refining learning tasks for AI reasoner agents.