RL Squeezes, SFT Expands: A Comparative Study of Reasoning LLMs (2509.21128v1)

Abstract: LLMs are typically trained by reinforcement learning (RL) with verifiable rewards (RLVR) and supervised fine-tuning (SFT) on reasoning traces to improve their reasoning abilities. However, how these methods shape reasoning capabilities remains largely elusive. Going beyond an accuracy-based investigation of how these two components sculpt the reasoning process, this paper introduces a novel analysis framework that quantifies reasoning paths and captures their qualitative changes under each training process (with models of 1.5B, 7B, and 14B parameters on mathematical domains). Specifically, we investigate the reasoning process at two levels of granularity: the trajectory-level, which examines complete reasoning outputs, and the step-level, which analyzes reasoning graphs whose nodes correspond to individual reasoning steps. Notably, clustering of unique reasoning trajectories shows complementary effects: RL compresses incorrect trajectories, whereas SFT expands correct ones. Step-level analysis reveals that RL steepens (about 2.5 times), while SFT flattens (reduced to about one-third), the decay rates of node visitation frequency, degree, and betweenness centrality distributions in the reasoning graph. This indicates that RL concentrates reasoning functionality into a small subset of steps, while SFT homogenizes it across many steps. Furthermore, by evaluating the reasoning graph topologies from multiple perspectives, we delineate the shared and distinct characteristics of RL and SFT. Our work presents a novel reasoning path perspective that explains why the current best practice of two-stage training, with SFT followed by RL, is successful, and offers practical implications for data construction and more efficient learning approaches.

• The paper demonstrates that RL compresses incorrect reasoning paths while SFT diversifies correct trajectories, leading to improved Pass@1 performance in mathematical LLMs.
• It employs a dual-level methodology by analyzing entire reasoning trajectories and individual reasoning steps with hierarchical clustering and graph-theoretic metrics across varying model scales.
• Findings imply that a two-stage SFT+RL approach optimally balances solution diversity and error suppression, offering actionable insights for future LLM training strategies.

RL Squeezes, SFT Expands: A Comparative Study of Reasoning LLMs

Introduction

This work provides a systematic, multi-granular analysis of how Reinforcement Learning (RL) with verifiable rewards (RLVR) and Supervised Fine-Tuning (SFT) on reasoning traces shape the reasoning processes of LLMs in mathematical domains. The paper moves beyond accuracy-based evaluation, introducing a framework that quantifies and characterizes the qualitative changes in reasoning paths induced by RL and SFT. The analysis is conducted at both the trajectory level (entire reasoning outputs) and the step level (reasoning graphs constructed from individual reasoning steps), across models of varying scale (1.5B, 7B, 14B parameters).

Trajectory-Level Analysis: Unique Reasoning Paths

The trajectory-level analysis investigates the diversity and structure of reasoning paths sampled from Base, RL, SFT, and SFT+RL models. For each model and problem, 256 samples are generated and clustered using chrF-based similarity and UPGMA hierarchical clustering to estimate the number of unique correct and incorrect trajectories.

Key findings:

• RL consistently reduces the number of unique incorrect trajectories (compresses error modes), regardless of whether it is applied to a Base or SFT model.
• SFT increases the number of unique correct trajectories (expands solution diversity), but preserves incorrect trajectories with non-negligible probability mass.
• The two-stage SFT+RL approach combines these effects: SFT introduces new correct solution strategies, and RL subsequently suppresses incorrect paths, maximizing Pass@1 performance.

  Figure 1: Effect of RL and SFT on the Number of Unique Trajectories. The x-axis represents the number of correct clusters and the y-axis represents the number of incorrect clusters for trajectories before and after training of 1.5B models.

This analysis provides a mechanistic explanation for the empirical success of SFT followed by RL, as seen in state-of-the-art mathematical LLMs. Notably, RL also reduces the number of correct trajectories, which explains why Base models can surpass RL models in Pass@k at large k, as previously observed in the literature.

Step-Level Analysis: Reasoning Graphs and Functional Topology

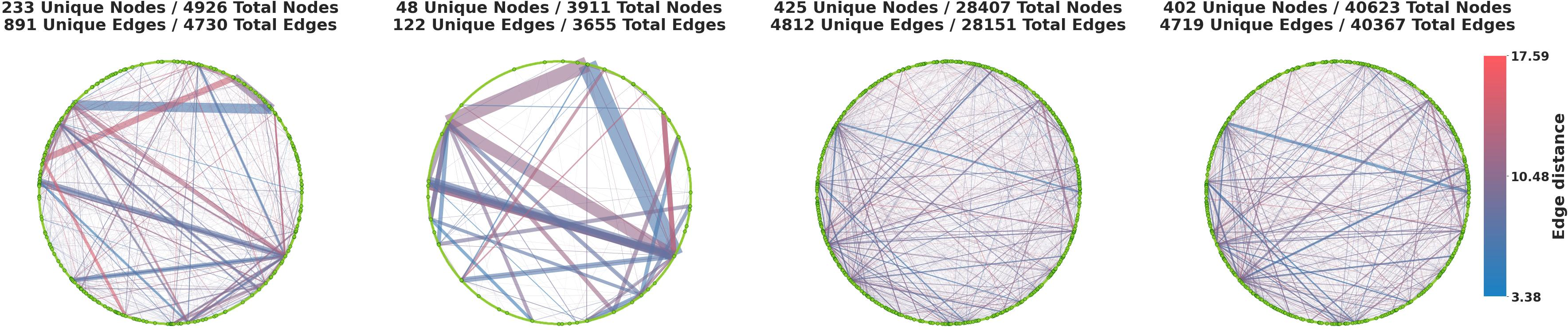
At the step level, the paper constructs reasoning graphs by segmenting model outputs into sentences, embedding them, and clustering into nodes. Each model's responses are mapped to paths in a shared graph, enabling direct comparison of graph-theoretic properties.

Global Structure:

• Rank plots of node visitation frequency, degree, and betweenness centrality follow exponential decay laws.
• RL steepens the decay rate (increases β by ~2.5x): reasoning is concentrated into a small subset of high-frequency, high-centrality nodes (functional hubs).
• SFT flattens the decay rate (reduces β to ~1/3): reasoning functionality is distributed more uniformly across many nodes.

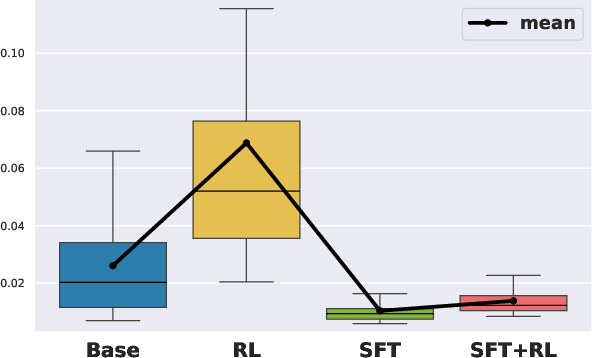
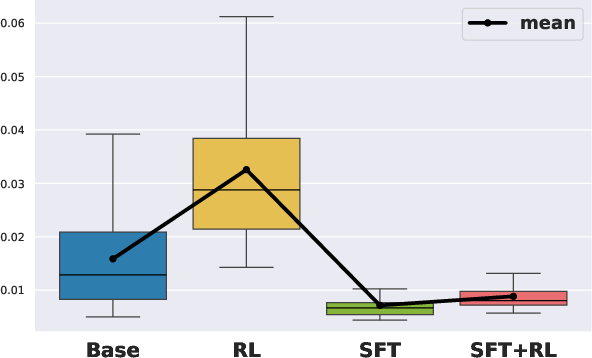
Figure 2: Exponential Decay Rate for Visitation Frequency, Degree, Betweenness Centrality. Box plots show the estimated exponential decay rate β across all problems in AIME24, AIME25, and AMC23 for the 1.5B models.

• RL transforms community-structured graphs (Base) into hub-centralized graphs with high edge density, low clustering, and high Freeman centralization.
• SFT and SFT+RL produce globally connected graphs with low modularity, high global efficiency, and high algebraic connectivity.

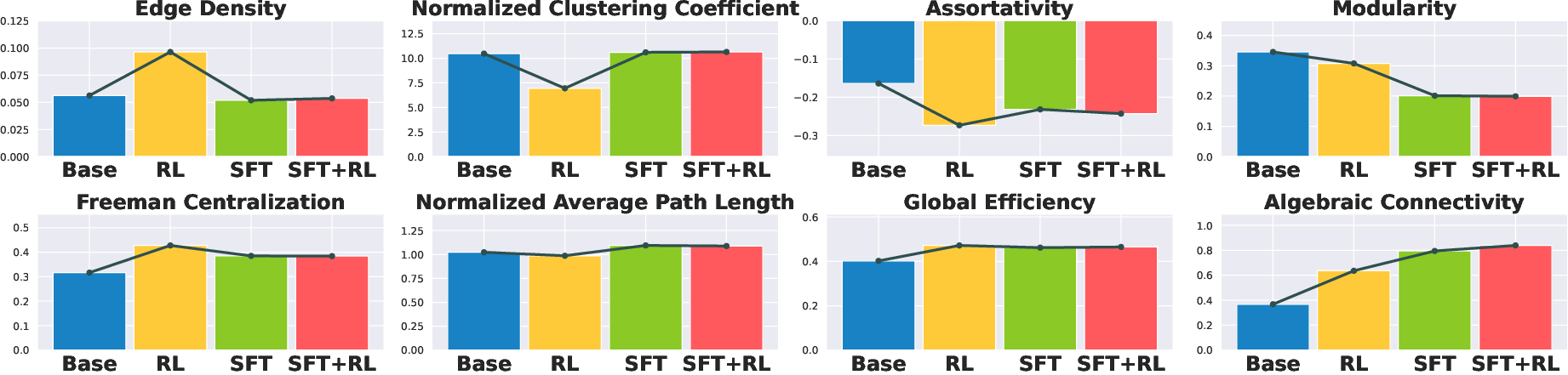
  Figure 3: Comparison of eight graph metrics across Base, RL, SFT, and SFT+RL models. Values are averaged across different model sizes.

Local Structure:

• Both RL and SFT increase the proportion of local cyclic subgraphs (graphlets), reflecting the emergence of backtracking and verification behaviors.
• Despite similar local graphlet statistics, substantial performance gaps remain between RL and SFT/SFT+RL models, indicating that global topology is more predictive of reasoning efficacy.

  Figure 4: Reasoning Graph Example. Directed reasoning graph for AIME24 Problem #1 built from 256 responses across the 7B models.

Empirical and Implementation Considerations

• Prompt and inference configuration: Model accuracy is highly sensitive to prompt templates and response length. For models generating lengthy reasoning, increasing max_model_len is critical to avoid truncation-induced degradation (see Figure 5).
• Sampling and clustering: For trajectory-level analysis, 256 samples per problem with temperature 0.6 and top_p 0.95 are used. Hierarchical clustering with chrF similarity thresholding is robust to metric and threshold choice.
• Graph construction: Sentence embeddings (BGE-large-en-v1.5, d=1024) and k-means clustering (K=2000) are used to define graph nodes. Graph-theoretic metrics are computed using NetworkX.
• Scaling: The analysis is performed across 1.5B, 7B, and 14B models, and on multiple mathematical datasets (AIME24, AIME25, AMC23), demonstrating the generality of the observed phenomena.

Theoretical and Practical Implications

• RL as a distributional sharpener: RLVR does not create new solution modes but reallocates probability mass, compressing both correct and incorrect trajectories. This supports theoretical results on support shrinkage and diversity collapse.
• SFT as a diversity expander: SFT introduces new correct solution strategies but does not suppress incorrect ones, explaining its tendency to improve Pass@k but not Pass@1.
• Two-stage SFT+RL: The complementary mechanisms of SFT and RL justify the widespread adoption of SFT followed by RL in high-performing reasoning LLMs.
• Graph-theoretic perspective: Concentration of reasoning into functional hubs (RL) versus distributed reasoning (SFT) provides a new lens for understanding generalization, memorization, and the emergence of cognitive behaviors such as backtracking.
• Data curation and training recipes: The findings suggest that SFT data should prioritize correct, diverse reasoning traces, while RL should be used to suppress incorrect modes. Step-level graph analysis can inform targeted RL on functional steps for more efficient learning.

Limitations and Future Directions

• The analysis is restricted to mathematical reasoning; extension to coding and scientific domains is warranted.
• The paper focuses on algorithmic differences between RL and SFT, not on dataset distribution shifts or robustness.
• Future work should investigate the impact of exploration bonuses in RL, the effect of distribution shift, and the application of graph-based metrics for dataset and curriculum design.

Conclusion

This paper provides a rigorous, multi-level analysis of how RL and SFT shape the reasoning processes of LLMs. RL compresses and concentrates reasoning, while SFT expands and diversifies it. The two-stage SFT+RL paradigm is empirically and theoretically justified by their complementary effects on reasoning path diversity and graph topology. The reasoning path and graph-theoretic framework introduced here offers actionable insights for the design, training, and evaluation of next-generation reasoning LLMs.