$ΔL$ Normalization: Rethink Loss Aggregation in RLVR (2509.07558v1)

Abstract: We propose $\Delta L$ Normalization, a simple yet effective loss aggregation method tailored to the characteristic of dynamic generation lengths in Reinforcement Learning with Verifiable Rewards (RLVR). Recently, RLVR has demonstrated strong potential in improving the reasoning capabilities of LLMs, but a major challenge lies in the large variability of response lengths during training, which leads to high gradient variance and unstable optimization. Although previous methods such as GRPO, DAPO, and Dr. GRPO introduce different loss normalization terms to address this issue, they either produce biased estimates or still suffer from high gradient variance. By analyzing the effect of varying lengths on policy loss both theoretically and empirically, we reformulate the problem as finding a minimum-variance unbiased estimator. Our proposed $\Delta L$ Normalization not only provides an unbiased estimate of the true policy loss but also minimizes gradient variance in theory. Extensive experiments show that it consistently achieves superior results across different model sizes, maximum lengths, and tasks. Our code will be made public at https://github.com/zerolllin/Delta-L-Normalization.

• The paper introduces ΔL Normalization, an unbiased estimator that minimizes gradient variance in RLVR by optimally aggregating losses.
• Empirical results demonstrate superior training stability and final accuracy on both CountDown and Math tasks compared to GRPO, DAPO, and Dr. GRPO.
• By incorporating a tunable hyperparameter α, the method balances variance reduction and effective utilization of long responses, ensuring easy integration with existing frameworks.

$\Delta L$ Normalization: Unbiased and Variance-Minimized Loss Aggregation for RLVR

Introduction

The paper introduces $\Delta L$ Normalization, a loss aggregation method designed for Reinforcement Learning with Verifiable Rewards (RLVR) in LLMs. RLVR has become a central paradigm for improving LLM reasoning, but it presents a unique challenge: the response trajectories generated during training vary widely in length, often spanning from tens to thousands of tokens. This variability induces high gradient variance, destabilizing optimization and impeding convergence. Existing aggregation strategies—such as GRPO, DAPO, and Dr. GRPO—attempt to mitigate this by normalizing losses with respect to response length, but they either introduce bias or fail to sufficiently control variance. The paper provides a theoretical and empirical analysis of these methods and proposes $\Delta L$ Normalization, which yields an unbiased, minimum-variance estimator for the policy gradient.

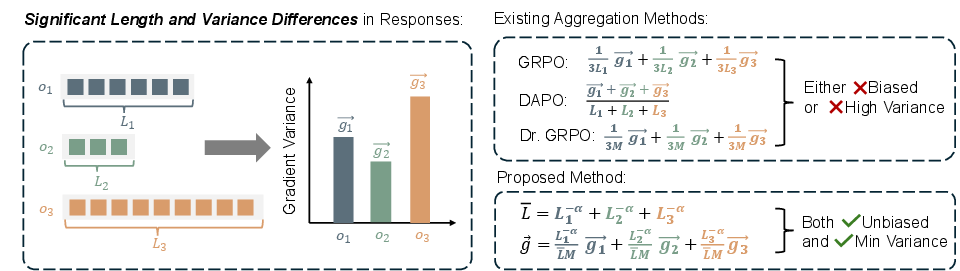
Figure 1: In RLVR, trajectory lengths vary significantly, and long trajectories induce high gradient variance, causing unstable training. Existing gradient aggregation methods either lead to biased updates or suffer from high variance. $\Delta L$ Normalization is both unbiased and variance-minimized.

Theoretical Analysis of Loss Aggregation in RLVR

Reformulation of Aggregation Methods

The policy gradient in RLVR is estimated from sampled trajectories, with each sample's gradient $\bm{g}_i$ corresponding to a response of length $L_i$. Standard estimators aggregate these gradients, but the variance of $\bm{g}_i$ grows linearly with $L_i$. GRPO normalizes each sample by $1/L_i$, DAPO normalizes by the sum of all $L_i$ in a batch, and Dr. GRPO uses a fixed constant. These choices have significant implications for the bias and variance of the resulting gradient estimator.

Gradient Variance and Length Dependence

Empirical and theoretical analysis confirms that the variance of the unnormalized gradient is proportional to response length. This is demonstrated by measuring the squared deviation of gradients for different response lengths, showing a clear linear relationship.

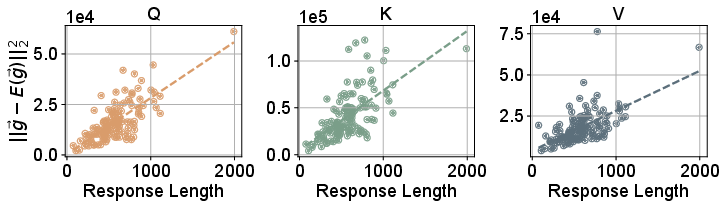
Figure 3: Deviation $||\bm{g}_i - \mathbb{E}[\bm{g}_i]||^2$ for a random sample on the Q, K, V projection in the last layer, confirming that gradient variance increases with response length.

Bias and Variance Properties

• GRPO and DAPO: Both introduce length-dependent bias. As response lengths increase, the effective gradient norm shrinks, slowing convergence.
• Dr. GRPO: Unbiased but exhibits high coefficient of variation (CV), leading to unstable training.
• Variance: High variance in gradient estimates leads to inefficient training and potential model collapse. The CV is lowest for GRPO, higher for DAPO and Dr. GRPO.

$\Delta L$ Normalization: Minimum-Variance Unbiased Aggregation

The paper formulates the aggregation problem as a minimum-variance unbiased estimation task. Given independent sample-level gradients $\bm{g}_i$ with variance proportional to $L_i$, the optimal unbiased linear combination is derived via Lagrange multipliers:

$$x_i^\star = \frac{1}{M} \frac{L_i^{-1}}{\sum_{j=1}^G L_j^{-1}}$$

A hyperparameter $\alpha \in [0,1]$ is introduced to interpolate between variance minimization ($\alpha=1$) and greater utilization of long responses ($\alpha<1$):

$$x_i = \frac{1}{M} \frac{L_i^{-\alpha}}{\sum_{j=1}^G L_j^{-\alpha}}$$

Key properties:

• Unbiasedness: For any $\alpha$, the estimator is unbiased.
• Minimum Variance: $\alpha=1$ yields the minimum possible variance.
• Controlled CV: Lower than DAPO and Dr. GRPO for all $\alpha$; matches GRPO at $\alpha=1$.
• Generalization: $\alpha=0$ recovers Dr. GRPO.

Empirical Evaluation

Experimental Setup

Experiments are conducted on Qwen2.5-3B and Qwen2.5-7B models, across CountDown and Math tasks, with maximum response lengths of 3072 and 8192. Baselines include GRPO Norm, DAPO Norm, Dr. GRPO Norm, and the original Dr. GRPO. All methods use the same advantage estimator for fair comparison.

Main Results

$\Delta L$ Normalization consistently outperforms all baselines in terms of stability and final accuracy across all settings.

Figure 2: Training dynamics of $\Delta L$ Normalization compared with baselines across tasks, model sizes, and maximum lengths. $\Delta L$ Normalization yields more stable training and higher accuracy.

• CountDown: Achieves the highest Avg@8 and Pass@8 scores. GRPO Norm is competitive early in training but stagnates due to bias, while $\Delta L$ Normalization continues to improve.
• Math: Outperforms all baselines on weighted average and mean Avg@8 across four datasets. Sudden increases in response length during training correlate with performance jumps, indicating effective utilization of long responses.

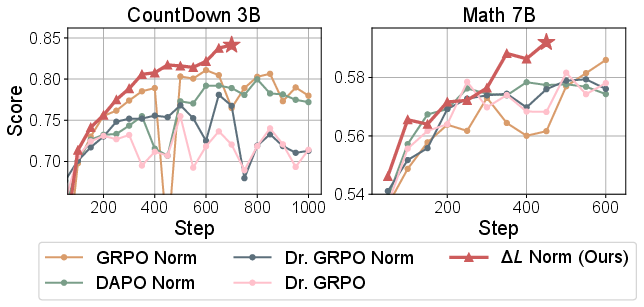
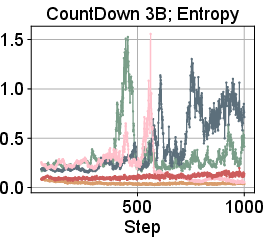
Figure 4: Selected training dynamics for CountDown and Math, showing monotonic improvement and stability for $\Delta L$ Normalization.

Combination with DAPO Techniques

When combined with DAPO's dynamic sampling and clipping, $\Delta L$ Normalization further improves performance, outperforming DAPO's overlong filtering and soft punishment strategies. Overlong filtering and soft punishment are less effective, sometimes even detrimental, confirming that variance control via aggregation is more robust.

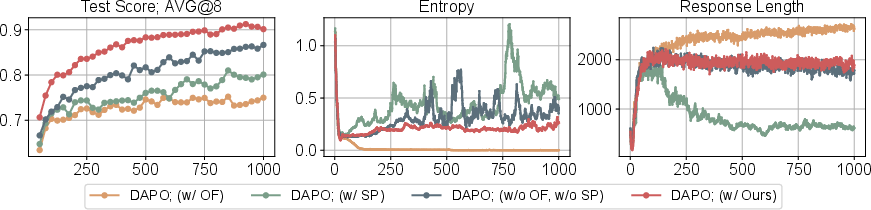
Figure 5: Comparison between $\Delta L$ Normalization and full DAPO on CountDown (3B model), showing superior performance for $\Delta L$ Normalization with dynamic sampling.

Hyperparameter Sensitivity

Performance is robust across $\alpha \in [0.5, 1.0]$, with $\alpha=1$ generally optimal except for Math, where $\alpha=0.75$ leverages long responses more effectively.

Implementation Considerations

• Code Simplicity: $\Delta L$ Normalization requires fewer than ten lines of code change in standard RLVR pipelines.
• Computational Overhead: Negligible, as the normalization weights are computed per batch.
• Hyperparameter Tuning: $\alpha$ can be set to 1 for most tasks; for tasks where long responses are particularly informative, $\alpha<1$ may yield further gains.
• Integration: Compatible with existing RLVR frameworks and orthogonal to reward shaping or auxiliary techniques.

Implications and Future Directions

$\Delta L$ Normalization provides a theoretically principled and empirically validated solution to the gradient variance problem in RLVR. By ensuring unbiasedness and minimizing variance, it enables more stable and efficient training of LLMs on tasks with highly variable response lengths. This approach is likely to generalize to other RL settings with variable-length trajectories and could be extended to multi-agent or hierarchical RL scenarios. Future work may explore adaptive schemes for $\alpha$, integration with advanced variance reduction techniques, and application to even larger models and more complex reasoning tasks.

Conclusion

$\Delta L$ Normalization addresses a fundamental challenge in RLVR by providing an unbiased, minimum-variance loss aggregation method. It consistently improves training stability and final model performance across tasks, model sizes, and response lengths, and is straightforward to implement. This work advances the theoretical understanding and practical methodology for RL-based LLM training, with broad implications for future research in scalable, stable reinforcement learning for LLMs.