Part I: Tricks or Traps? A Deep Dive into RL for LLM Reasoning (2508.08221v1)

Abstract: Reinforcement learning for LLM reasoning has rapidly emerged as a prominent research area, marked by a significant surge in related studies on both algorithmic innovations and practical applications. Despite this progress, several critical challenges remain, including the absence of standardized guidelines for employing RL techniques and a fragmented understanding of their underlying mechanisms. Additionally, inconsistent experimental settings, variations in training data, and differences in model initialization have led to conflicting conclusions, obscuring the key characteristics of these techniques and creating confusion among practitioners when selecting appropriate techniques. This paper systematically reviews widely adopted RL techniques through rigorous reproductions and isolated evaluations within a unified open-source framework. We analyze the internal mechanisms, applicable scenarios, and core principles of each technique through fine-grained experiments, including datasets of varying difficulty, model sizes, and architectures. Based on these insights, we present clear guidelines for selecting RL techniques tailored to specific setups, and provide a reliable roadmap for practitioners navigating the RL for the LLM domain. Finally, we reveal that a minimalist combination of two techniques can unlock the learning capability of critic-free policies using vanilla PPO loss. The results demonstrate that our simple combination consistently improves performance, surpassing strategies like GRPO and DAPO.

• The paper provides a systematic evaluation of RL techniques for LLM reasoning using controlled experiments and an open-source framework.
• It demonstrates that group-level normalization and clip-higher strategies boost stability, diversity, and overall model performance.
• The study introduces Lite PPO, a minimalist approach that outperforms complex RL pipelines across varied model types.

Dissecting Reinforcement Learning Techniques for LLM Reasoning: Mechanistic Insights and Practical Guidelines

Introduction and Motivation

The application of reinforcement learning (RL) to LLM reasoning tasks has led to a proliferation of optimization techniques, each with distinct theoretical motivations and empirical claims. However, the lack of standardized guidelines and the presence of contradictory recommendations have created significant barriers to practical adoption. This work provides a systematic, reproducible evaluation of widely used RL techniques for LLM reasoning, focusing on normalization, clipping, filtering, and loss aggregation. The paper leverages a unified open-source framework and a controlled experimental setup to isolate the effects of each technique, offering actionable guidelines and challenging the necessity of complex, technique-heavy RL pipelines.

Figure 1: The proliferation of RL optimization techniques and the establishment of detailed application guidelines via mechanistic dissection and the introduction of Lite PPO.

Experimental Design and Baseline Analysis

The experiments are conducted using the ROLL framework with Qwen3-4B and Qwen3-8B models, both in base (non-aligned) and aligned (instruction-tuned) variants. Training is performed on open-source mathematical reasoning datasets of varying difficulty, and evaluation spans six math benchmarks. The baseline analysis reveals that model alignment and data difficulty significantly affect learning dynamics. Aligned models exhibit higher initial accuracy and longer responses but show limited improvement from further RL, indicating diminishing returns for already optimized policies.

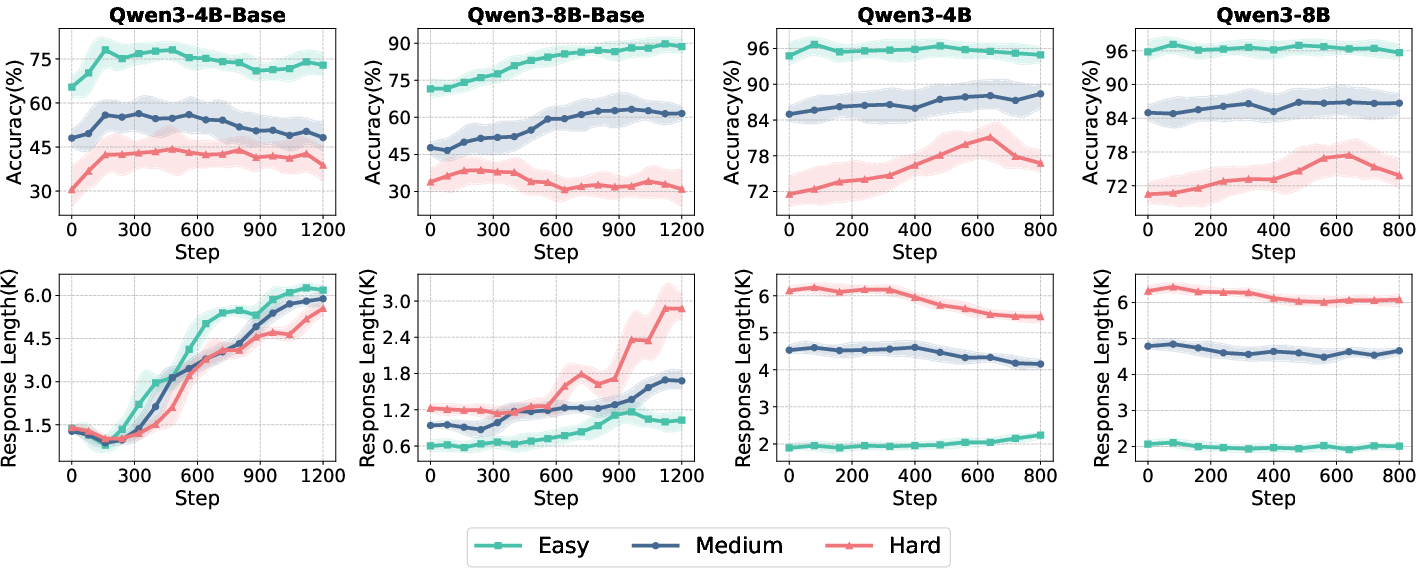
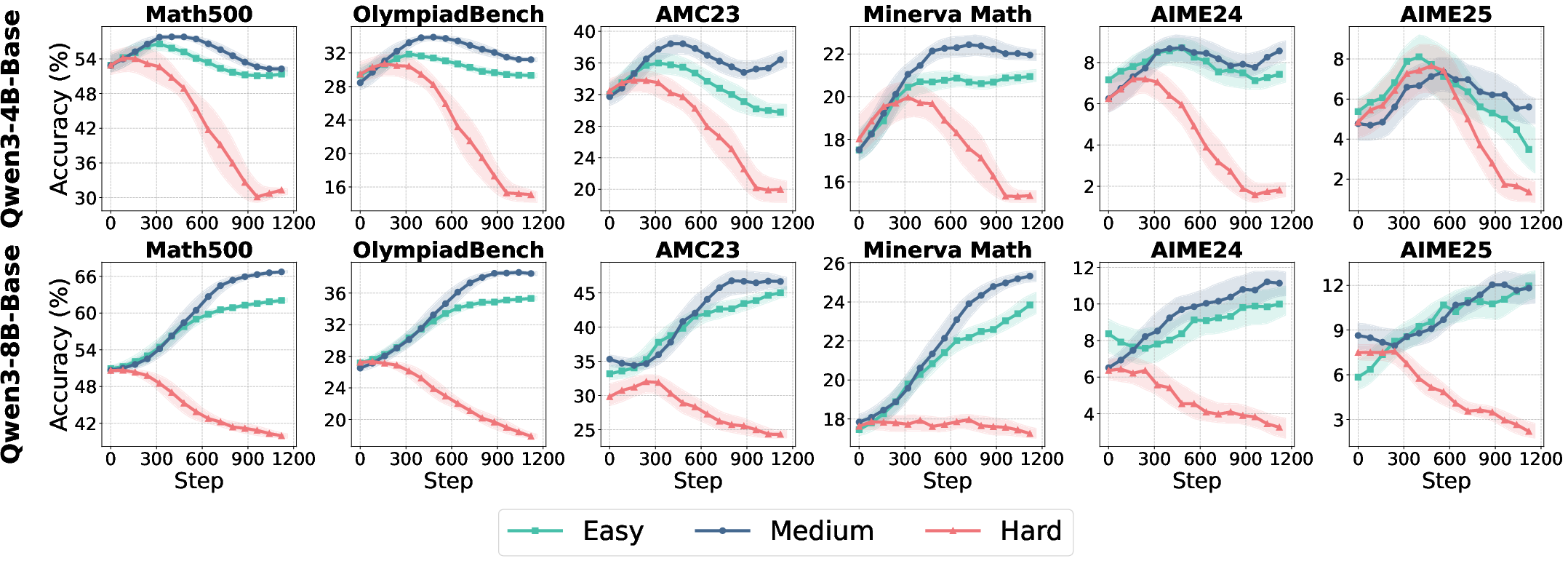
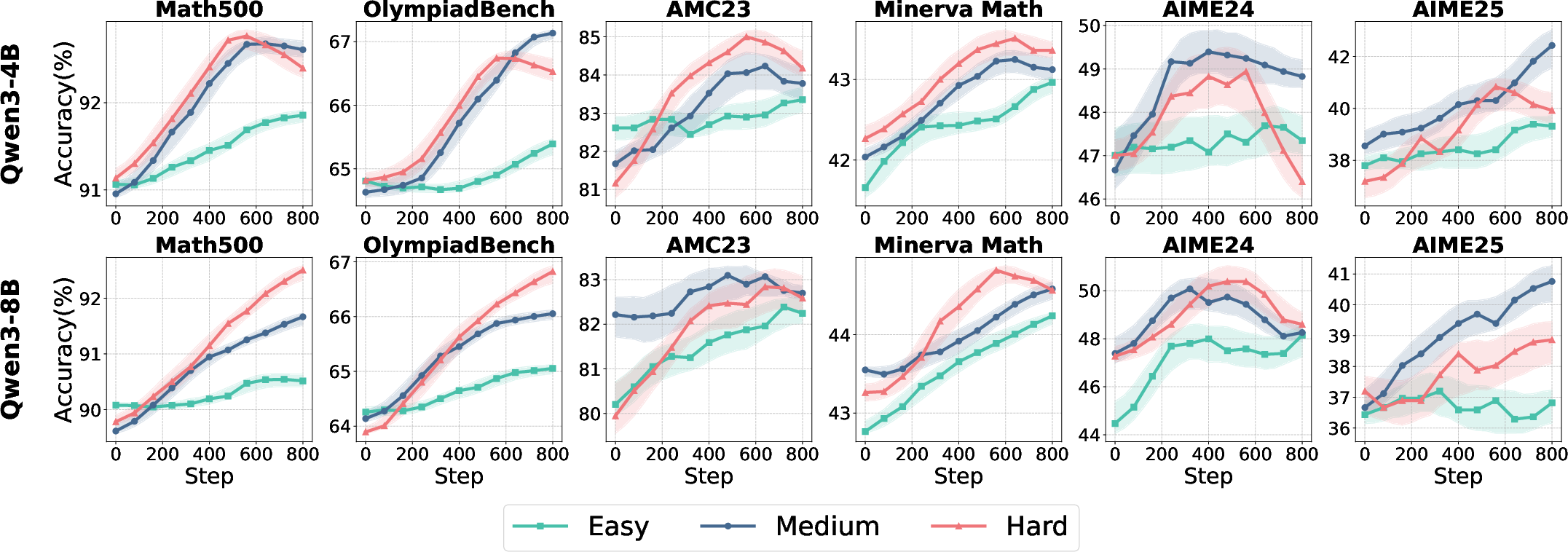
Figure 2: Test accuracy and response length trajectories for Qwen3-4B/8B (Base and Aligned) across data difficulties, highlighting the impact of alignment and task complexity.

Mechanistic Analysis of RL Techniques

Advantage Normalization

Advantage normalization is critical for variance reduction and stable policy optimization. The paper contrasts group-level normalization (within-prompt) and batch-level normalization (across batch), demonstrating that group-level normalization is robust across reward settings, while batch-level normalization is highly sensitive to reward scale and can induce instability under concentrated reward distributions.

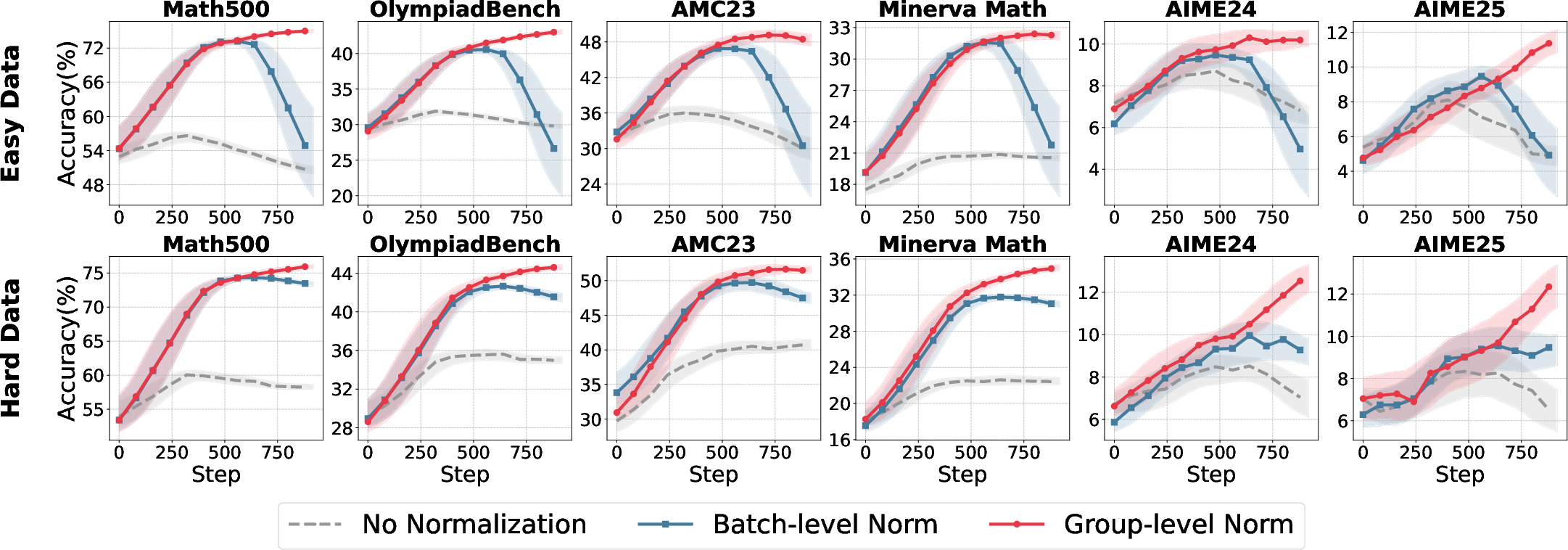
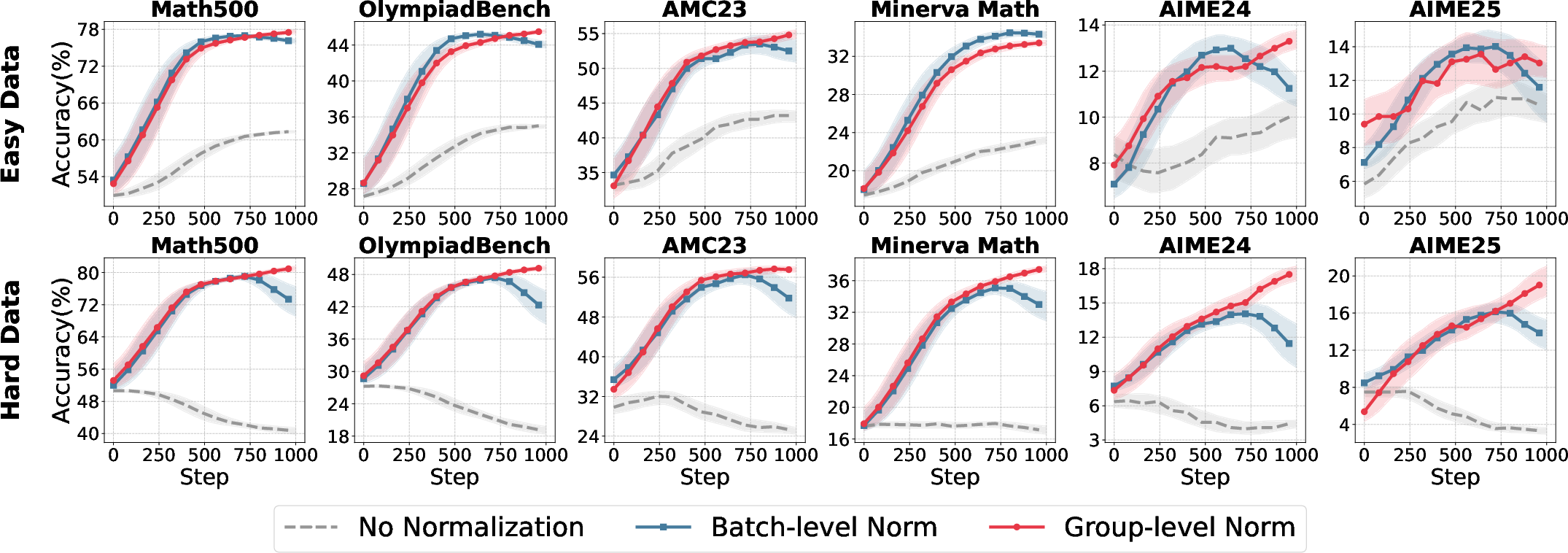
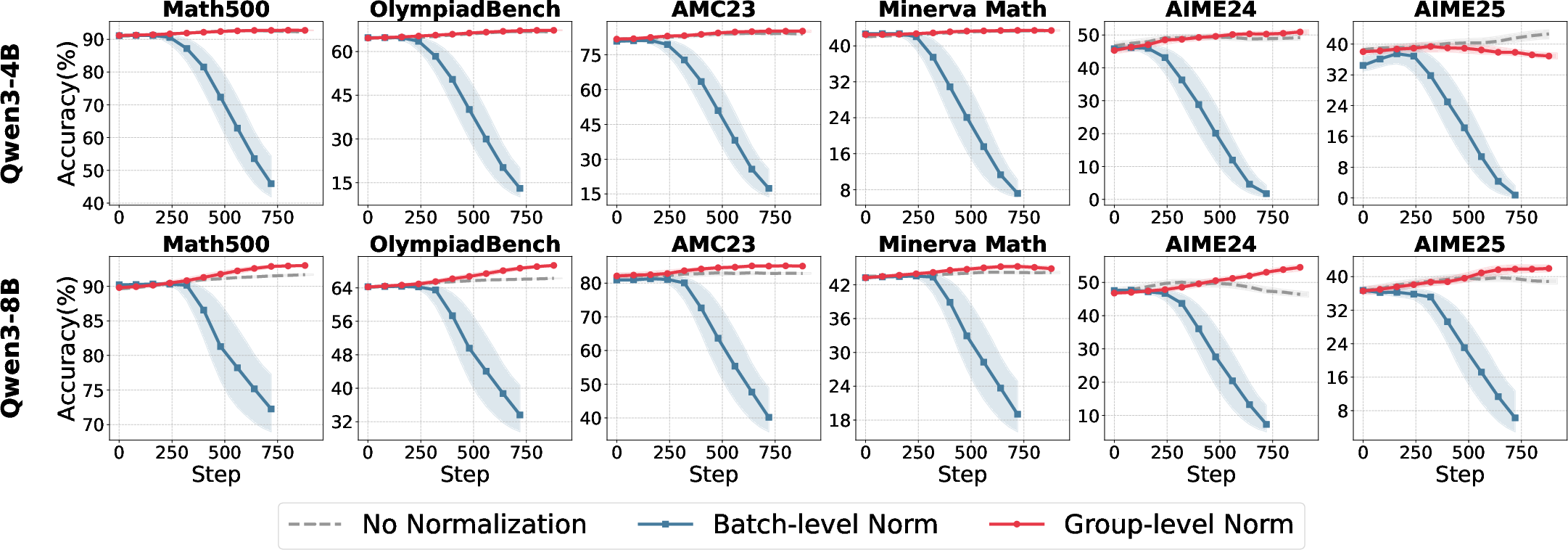
Figure 3: Comparative accuracy over training iterations for different normalization strategies and model sizes, showing group-level normalization's robustness.

When the reward scale is increased (e.g., $R \in \{-1, 1\}$), batch-level normalization regains effectiveness, underscoring the interaction between normalization and reward design.

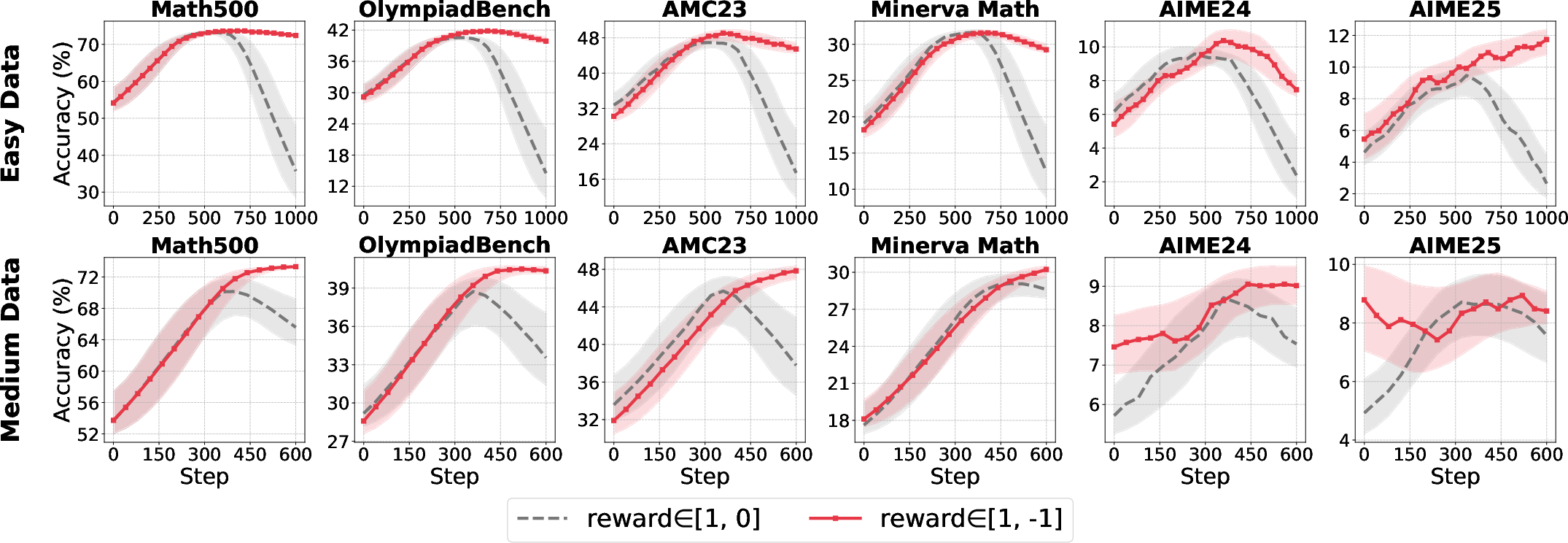
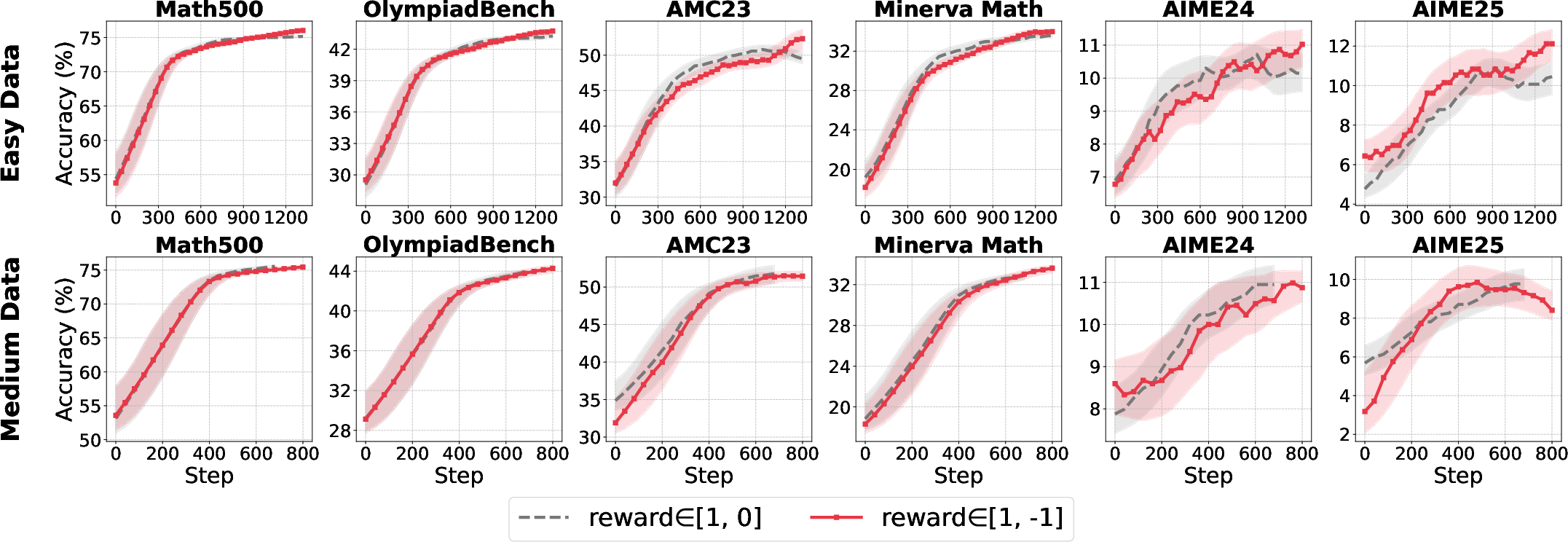
Figure 4: Sensitivity of batch- and group-level normalization to reward scale, with batch-level normalization benefiting from larger reward variance.

Ablation on the standard deviation term in normalization reveals that omitting the standard deviation in highly concentrated reward settings prevents gradient explosion and stabilizes training.

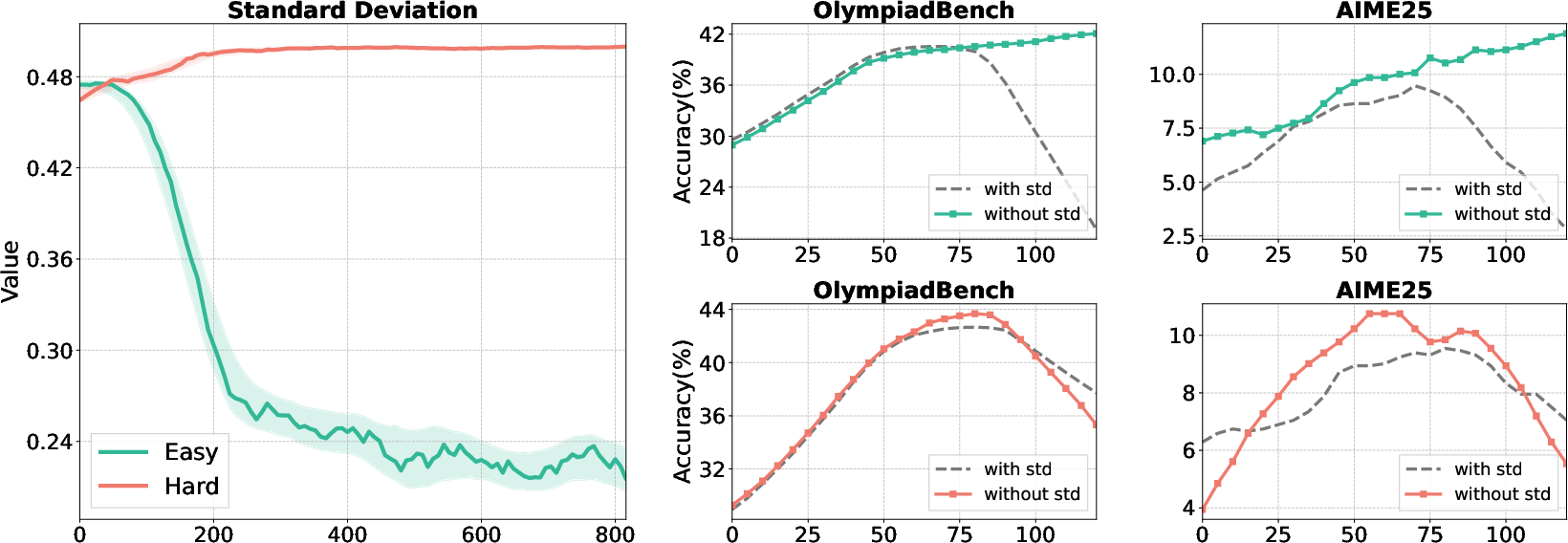
Figure 5: Left: Standard deviation collapse in easy datasets. Right: Removing std from normalization stabilizes accuracy in concentrated reward regimes.

A hybrid approach—using group-level mean and batch-level standard deviation—yields the most robust normalization, effectively balancing local competition and global variance control.

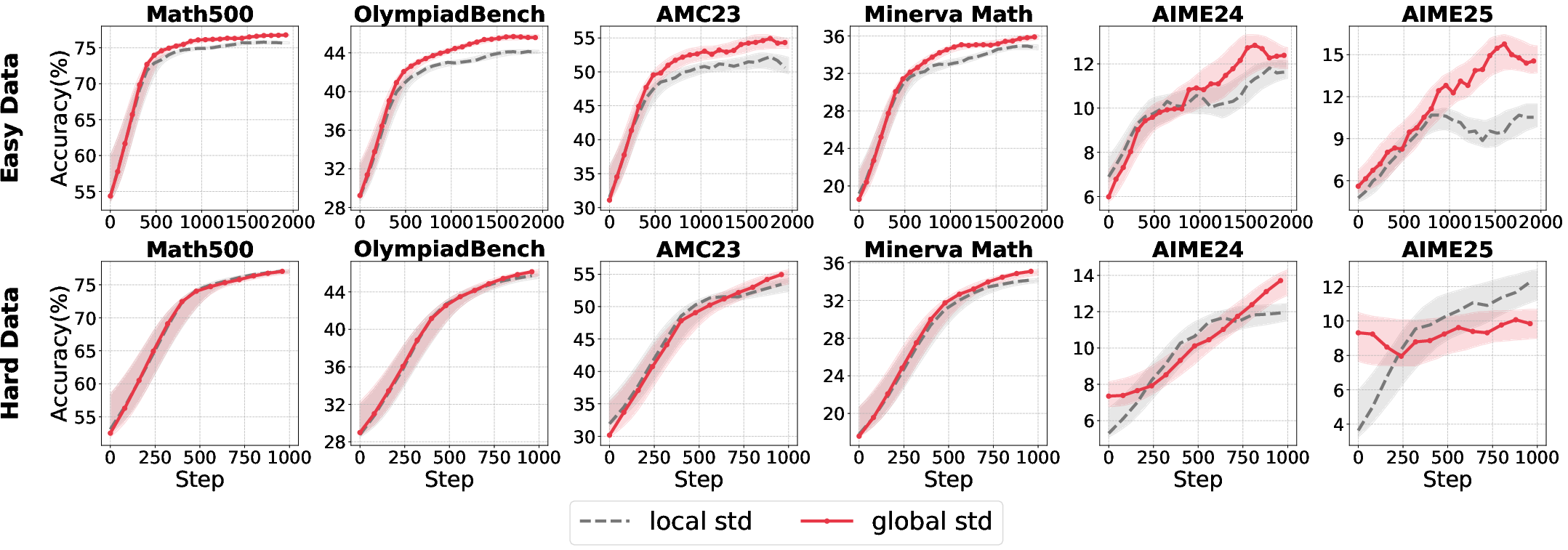
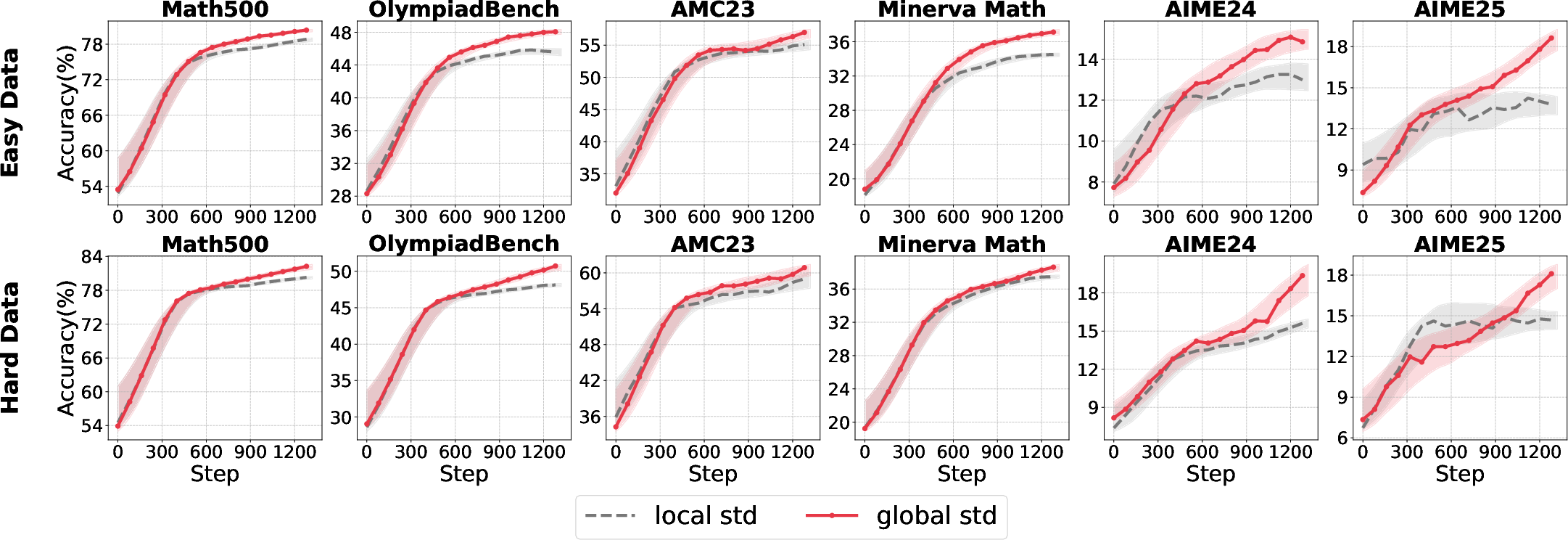
Figure 6: Superior performance of group-mean/batch-std normalization across model sizes and data difficulties.

Clipping Strategies: Clip-Higher

The standard PPO clipping mechanism can induce entropy collapse, especially in LLMs, by suppressing low-probability tokens and reducing exploration. The Clip-Higher variant relaxes the upper bound, mitigating entropy loss and enabling more diverse policy updates, particularly in aligned models with higher reasoning capacity.

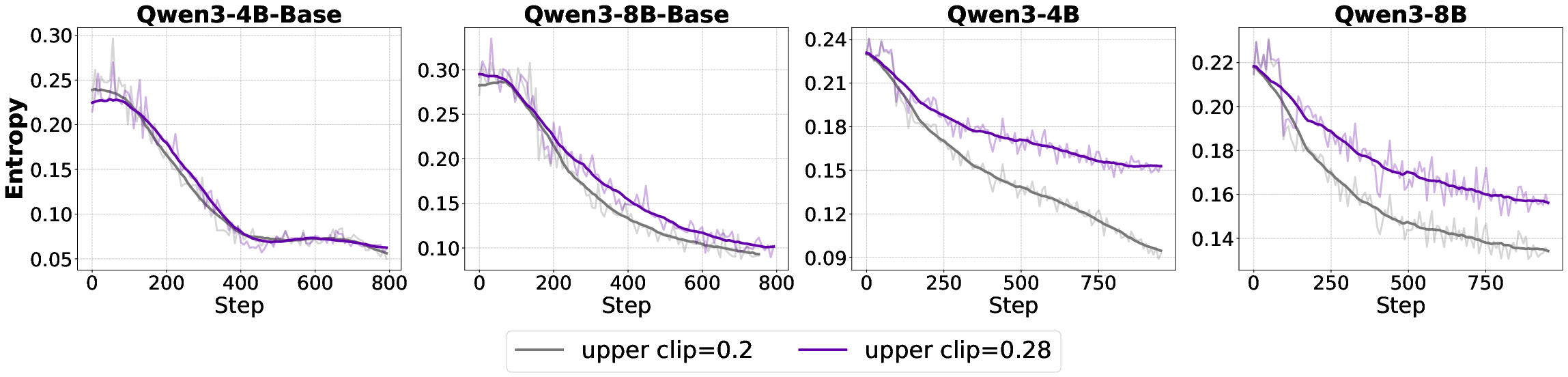
Figure 7: Entropy trajectories under different clip upper bounds, with higher bounds preserving entropy in aligned models.

Empirical results show that increasing the clip upper bound benefits aligned models but has negligible or negative effects on base models, due to their limited expressiveness and low policy deviation.

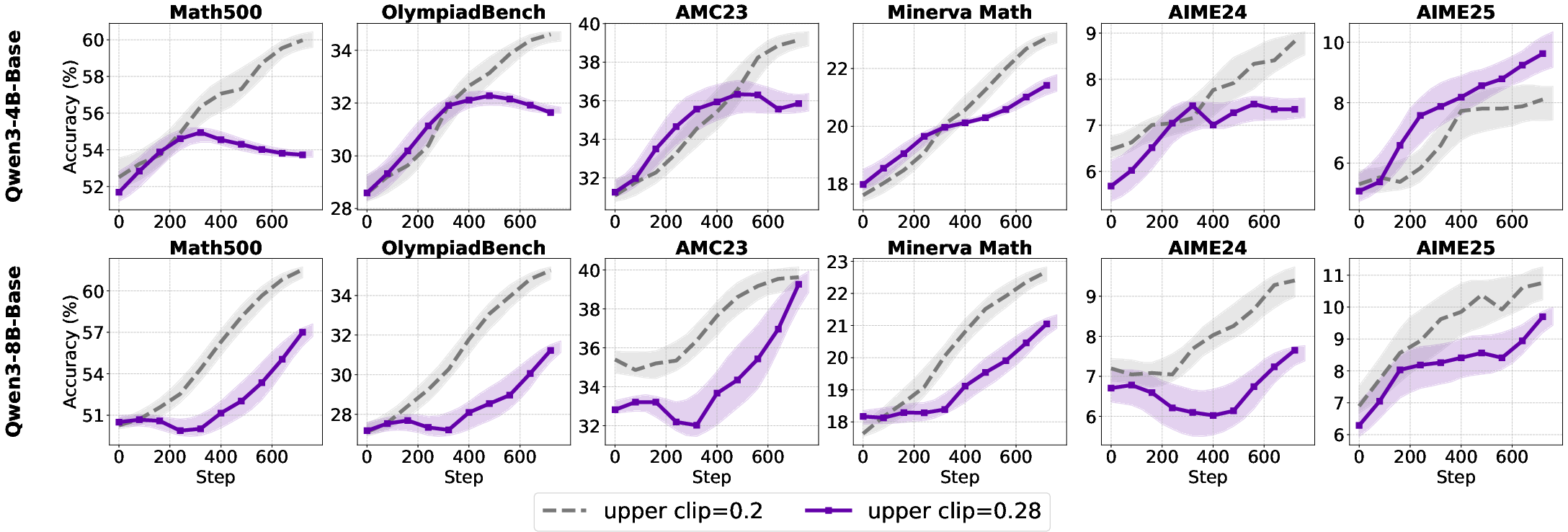
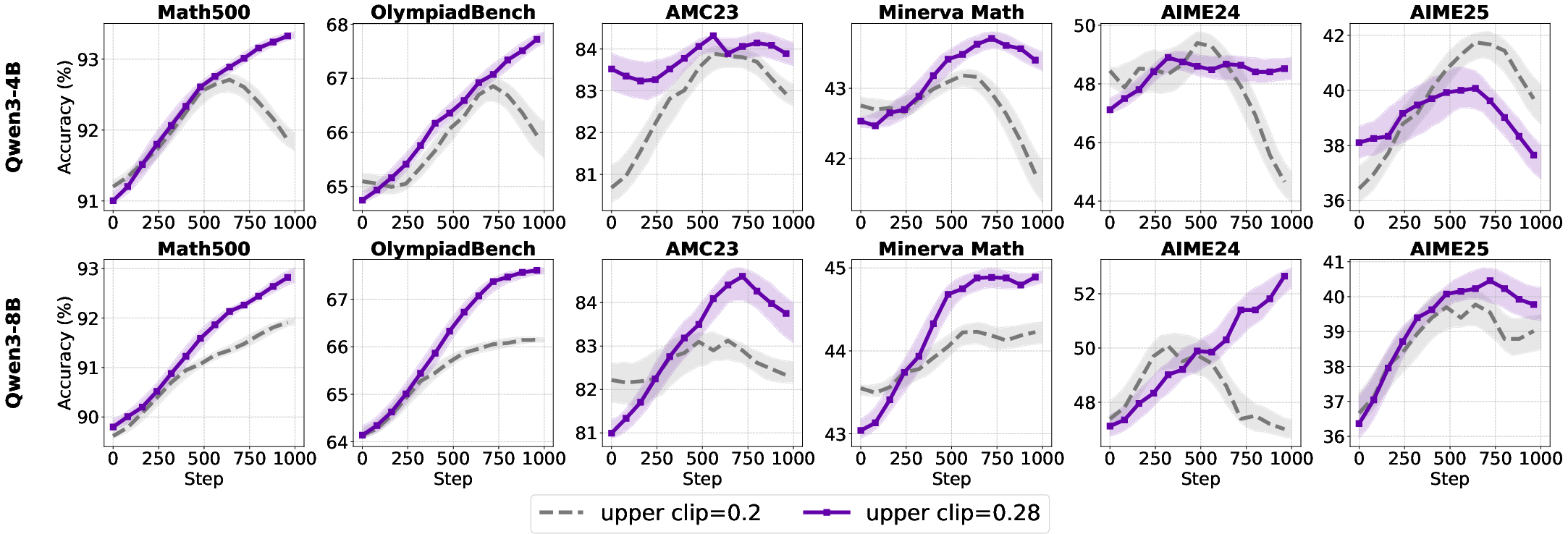
Figure 8: Test accuracy under varying clip upper bounds, highlighting model-dependent effects.

Token-level analysis reveals that stricter clipping disproportionately affects discourse connectives, potentially restricting the model's ability to generate innovative reasoning structures. Relaxing the upper bound shifts clipping to high-frequency function words, promoting structural diversity.

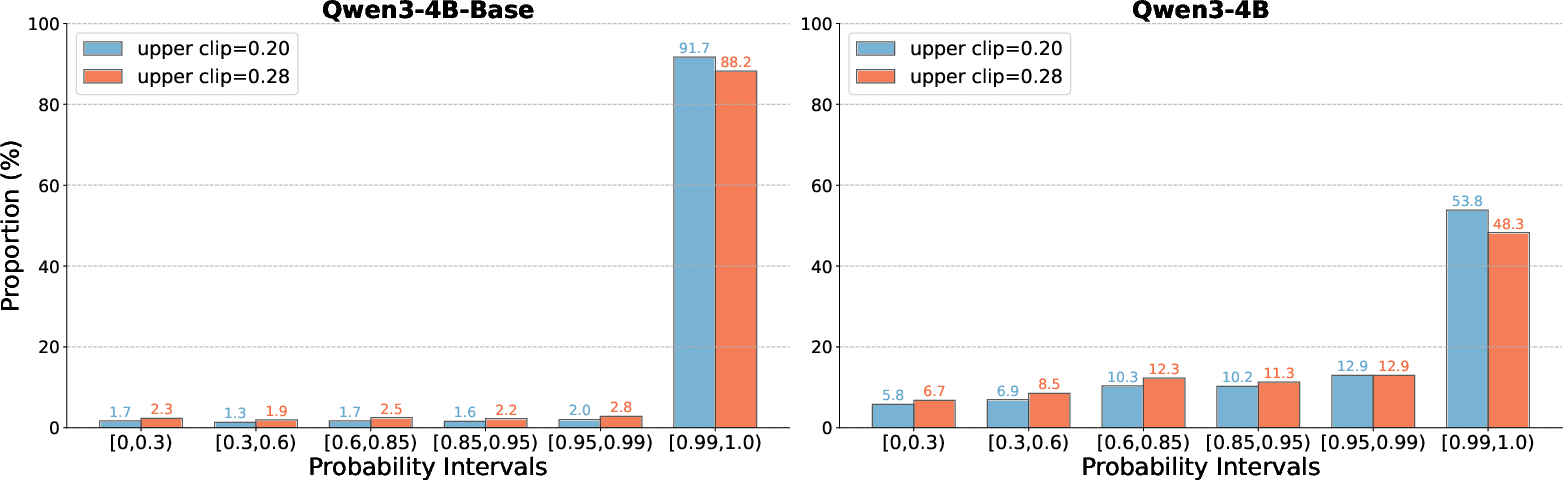
Figure 9: Probability distributions for Qwen3-4B-Base and Qwen3-4B under different clip upper bounds, illustrating the effect on token diversity.

Figure 10: Case paper of clipping effects on token selection and discourse structure.

A scaling law is observed for small models: performance improves monotonically with higher clip upper bounds, peaking at 0.32, whereas larger models exhibit a non-monotonic relationship, with optimal performance at intermediate values.

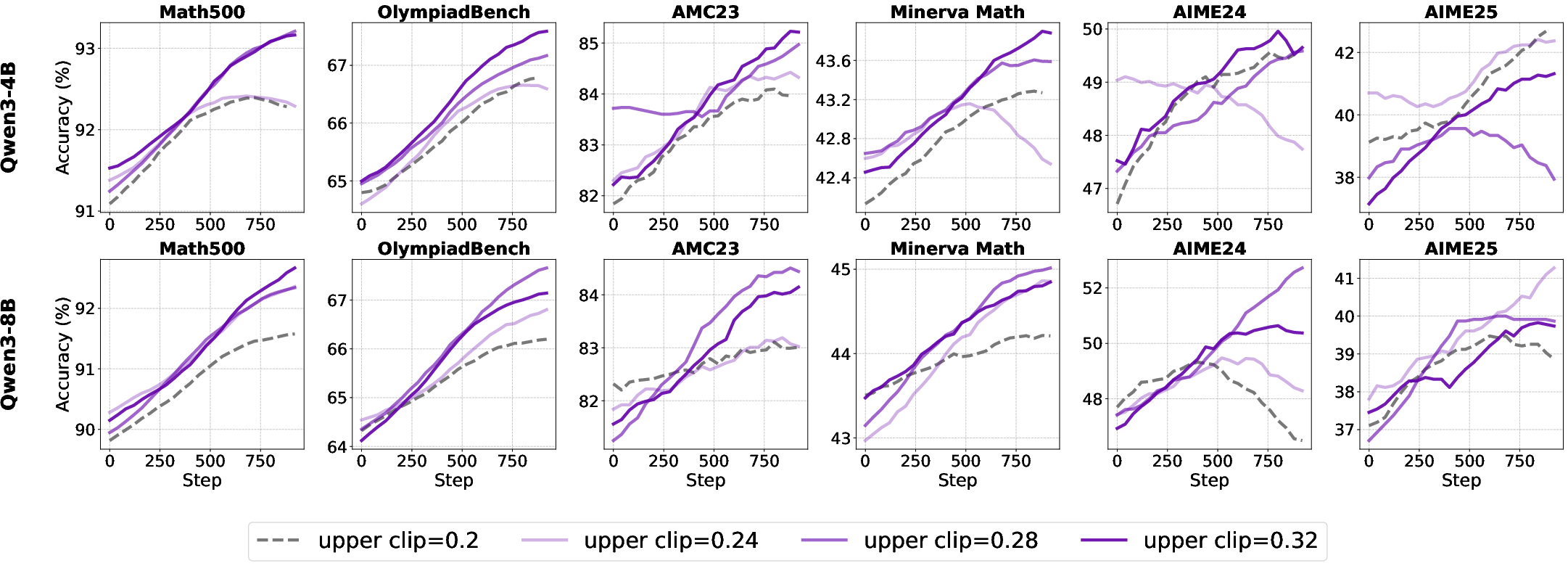
Figure 11: Scaling law between clip upper bound and accuracy for different model sizes.

Loss Aggregation Granularity

Loss aggregation at the token level, as opposed to the sequence level, ensures equal contribution from each token and mitigates length bias. Token-level aggregation is particularly effective for base models, improving convergence and robustness, but offers limited or negative gains for aligned models, where sequence-level aggregation better preserves output structure.

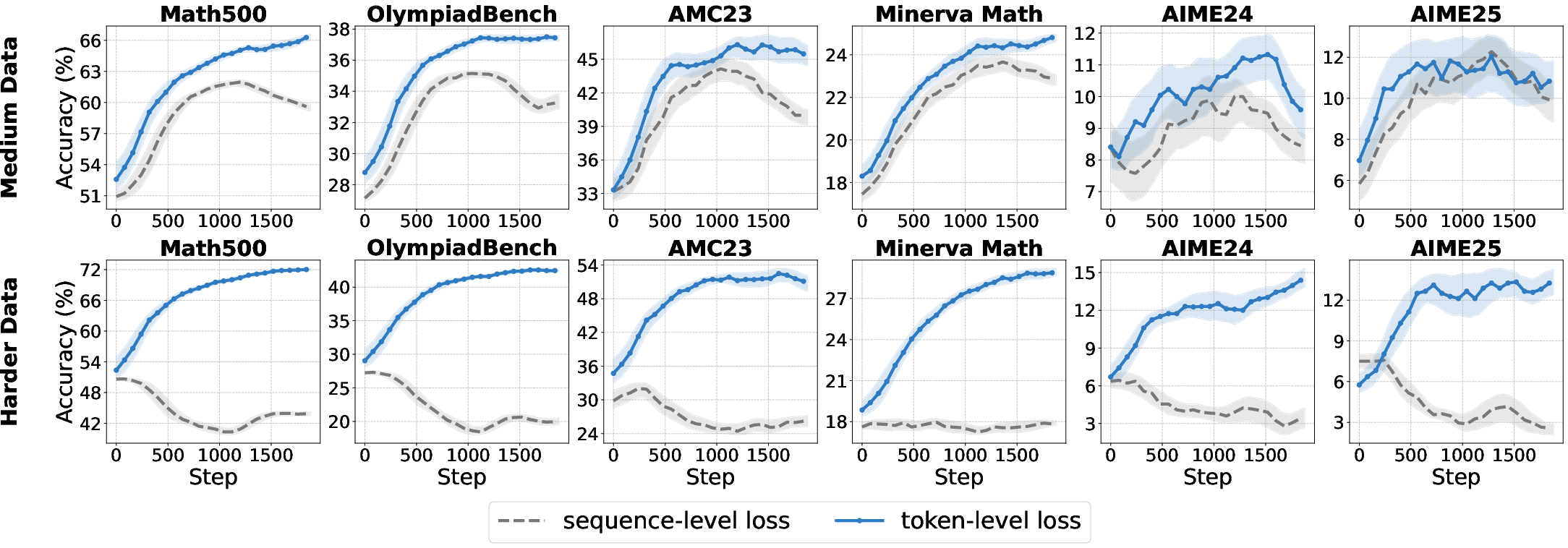
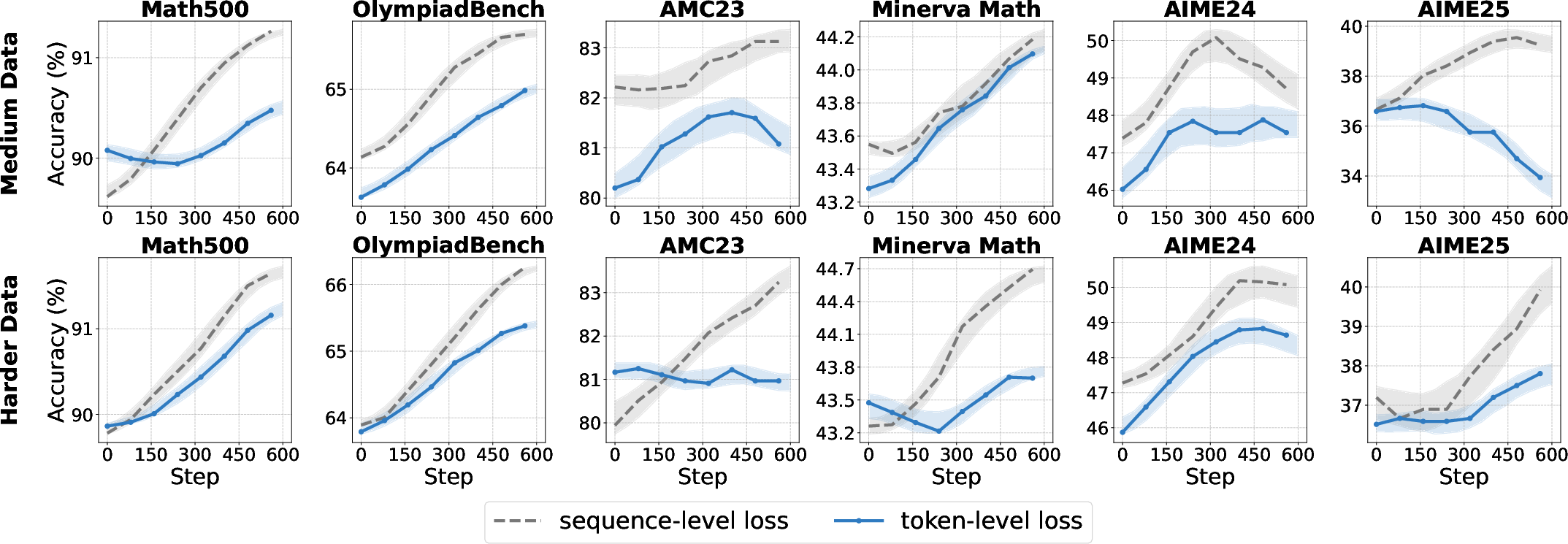
Figure 12: Token-level loss aggregation outperforms sequence-level for base models but not for aligned models.

Overlong Filtering

Overlong filtering, which masks rewards for excessively long responses, is effective for short-to-medium reasoning tasks but provides limited benefit for long-tail reasoning. Its utility diminishes as the maximum generation length increases, and it primarily filters degenerate, repetitive outputs in high-length regimes.

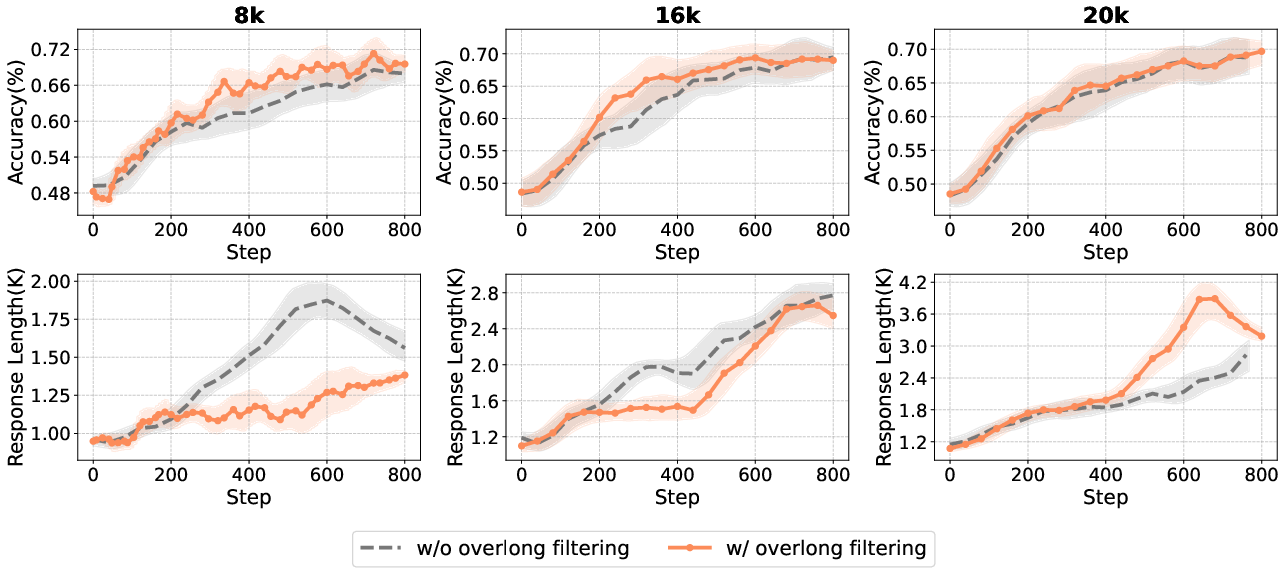
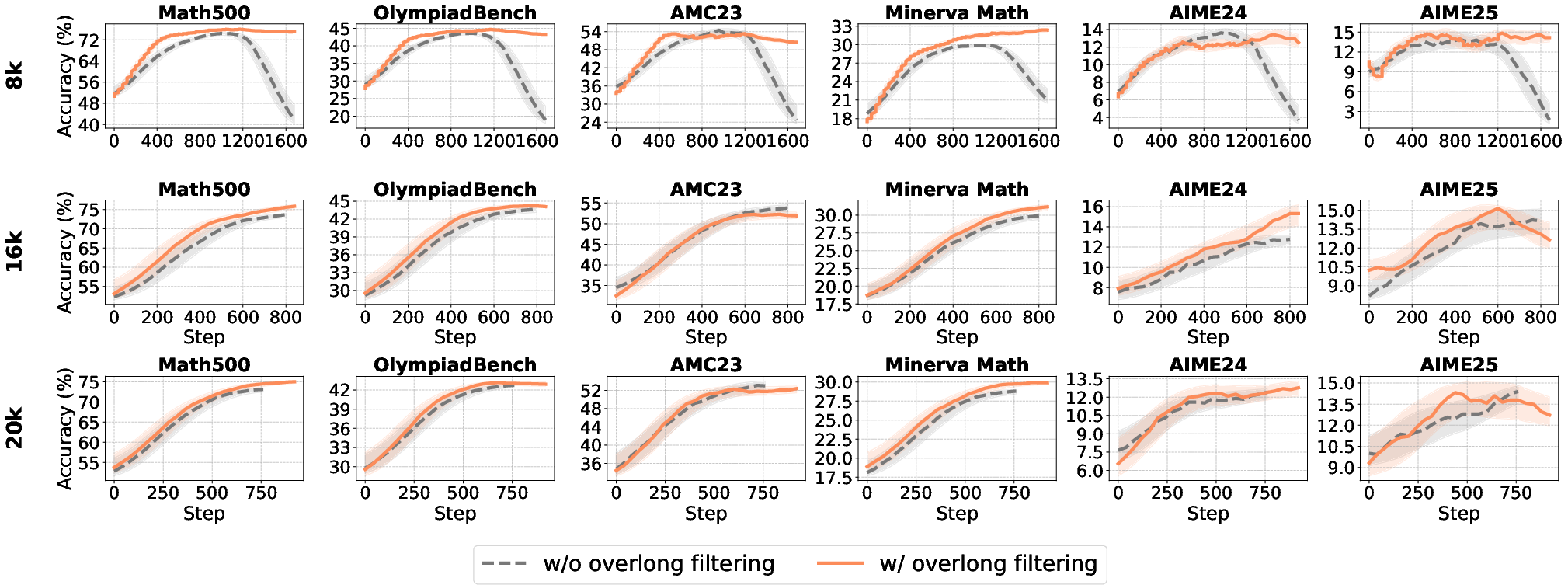
Figure 13: Impact of maximum generation length and overlong filtering on accuracy and response length.

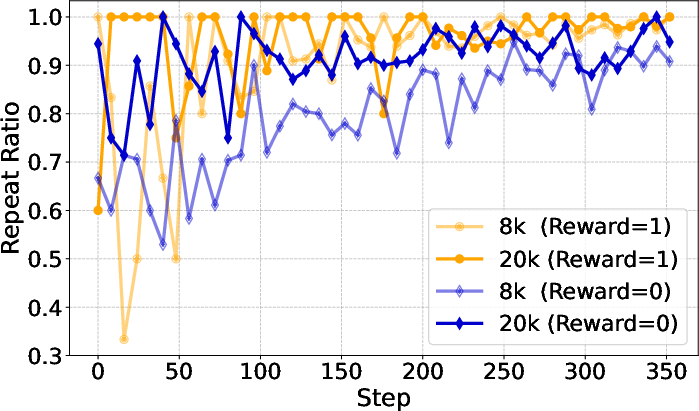
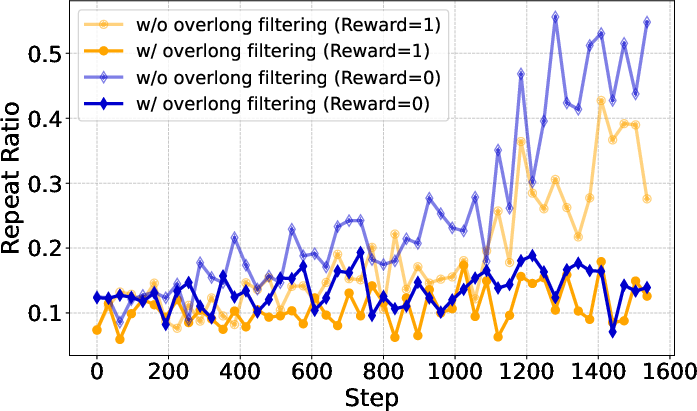
Figure 14: Repeat ratio analysis for different generation lengths and filtering strategies, showing reduction in degenerate outputs.

Minimalist RL: Lite PPO

Synthesizing the mechanistic insights, the paper proposes Lite PPO—a minimalist combination of group-mean/batch-std advantage normalization and token-level loss aggregation, applied to critic-free PPO. Lite PPO consistently outperforms more complex algorithms such as GRPO and DAPO, especially on non-aligned models and across data difficulties.

Figure 15: Lite PPO achieves superior accuracy and stability compared to GRPO and DAPO on non-aligned models.

Implications and Future Directions

This work demonstrates that many widely adopted RL techniques for LLM reasoning are highly sensitive to model type, reward design, and data distribution. The findings challenge the necessity of complex, over-engineered RL pipelines, showing that a principled, minimalist approach can yield superior empirical performance. The paper also highlights the importance of transparency and reproducibility, advocating for open-source frameworks and detailed reporting to facilitate cross-family generalization and community progress.

Theoretically, the results suggest that RL4LLM optimization should be contextualized, with technique selection tailored to model alignment, reward sparsity, and task structure. Practically, the guidelines provided here can streamline RL4LLM deployment, reduce engineering overhead, and improve reproducibility.

Future research should focus on extending these analyses to other LLM families, further unifying RL frameworks, and exploring additional minimalist algorithmic combinations. The development of standardized, modular RL toolkits will be critical for advancing both academic and industrial applications of RL4LLM.

Conclusion

This comprehensive dissection of RL techniques for LLM reasoning resolves key ambiguities in the field, providing mechanistic understanding and practical guidelines for technique selection. The empirical evidence supports the claim that simplicity, when grounded in principled analysis, can outperform complexity in RL4LLM optimization. The work sets a foundation for standardized, efficient, and robust RL pipelines, and calls for increased transparency to bridge the gap between academic research and industrial practice.