Self-Questioning Language Models (2508.03682v2)

Abstract: Can LLMs improve without external data -- by generating their own questions and answers? We hypothesize that a pre-trained LLM can improve its reasoning skills given only a single prompt specifying the topic (e.g., algebra word problems) and asking the model to generate its own questions. To do this, we propose Self-Questioning LLMs (SQLM): an asymmetric self-play framework where a proposer is given the topic and generates a question for a solver, who tries to answer it. Both the proposer and solver are trained via reinforcement learning. The proposer receives a reward if the problem is not too easy or too difficult, and the solver receives a reward based on majority voting, a proxy for correctness in the absence of ground-truth answers. For coding, the proposer can instead generate unit tests which are used for verification. We study this asymmetric self-play framework on three benchmarks: three-digit multiplication, algebra problems from the OMEGA benchmark, and programming problems from Codeforces. By continually generating more interesting problems and attempting to solve them, LLMs can improve on downstream benchmarks without access to any curated training datasets.

• The paper introduces a novel self-supervised framework where LLMs generate and solve their own problems using asymmetric self-play, eliminating the need for curated data.
• It implements a minimax RL game between a proposer generating problems and a solver verifying answers, achieving up to 16% performance gains on benchmarks.
• The method significantly improves data diversity and adaptive curriculum generation in arithmetic, algebra, and coding tasks, paving a scalable path for LLM refinement.

Self-Questioning LLMs: Autonomous Self-Improvement via Asymmetric Self-Play

Introduction and Motivation

The paper "Self-Questioning LLMs" (SQLM) (2508.03682) addresses a central bottleneck in post-training LLMs: the reliance on hand-curated datasets for both questions and answers. While unsupervised reward functions have reduced the need for labeled answers, the generation of high-quality, diverse, and challenging questions remains a labor-intensive process. SQLM proposes a fully self-supervised framework in which a pre-trained LLM iteratively improves its reasoning abilities by generating and solving its own problems, without any curated training data or labeled answers.

The core innovation is the application of asymmetric self-play—originally developed for goal-conditioned RL in robotics—to the domain of LLM post-training. In this setup, the LLM is split into two roles: a proposer, which generates new problems, and a solver, which attempts to solve them. Both are trained via RL, with carefully designed reward functions to ensure the generated problems are neither trivial nor unsolvable. This framework is evaluated on arithmetic, algebra, and code generation tasks, demonstrating that LLMs can bootstrap improved reasoning capabilities solely through self-generated content.

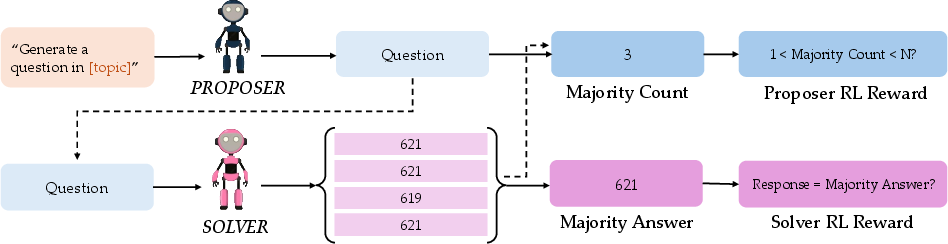
Figure 1: Overview of the SQLM framework, where a single prompt seeds the proposer, which generates a question; the solver attempts to answer, and rewards are computed via majority voting or test-case verification.

Methodology

Asymmetric Self-Play for LLMs

The SQLM framework formalizes the interaction between proposer and solver as a minimax RL game. The proposer $\pi_P$ generates a problem $x$ conditioned on a topic $t$, and the solver $\pi_S$ attempts to solve $x$. Both policies are updated via RL to maximize their respective expected rewards:

• Solver reward: Encourages correct solutions, using majority voting (for arithmetic/algebra) or test-case pass rate (for code).
• Proposer reward: Encourages generation of problems that are neither too easy (all solver outputs agree) nor too hard (no agreement or all test cases fail).

This setup is fully self-supervised: no external data, labels, or verifiers are required. The only input is a single prompt specifying the domain (e.g., "algebra word problems").

Reward Design

• Small generator-verifier gap (e.g., arithmetic, algebra):
  • For each problem, $N$ solver outputs are sampled.
  • The majority answer is used as a proxy for correctness.
  • Solver reward: 1 if output matches the majority, 0 otherwise.
  • Proposer reward: 1 if $0 < \#$majority matches $< N$; 0 otherwise.
• Large generator-verifier gap (e.g., code):
  • Proposer generates both the problem and a set of unit tests.
  • Solver reward: Fraction of test cases passed.
  • Proposer reward: 1 if $0 <$ fraction passed $< 1$; 0 otherwise.

This reward structure ensures a curriculum of problems that adapt to the solver's current capabilities, driving both roles to improve iteratively.

Implementation and Training

The SQLM framework is implemented on top of the verl RLHF library, using Qwen2.5-3B-Instruct and Qwen2.5-Coder-3B-Instruct as base models. Key hyperparameters include a proposer update frequency (default: every 5 steps), batch size of 64, and a learning rate of $1 \times 10^{-6}$. For each task, only a single prompt is provided; no example problems or answers are given.

Experimental Results

Quantitative Performance

SQLM is evaluated on three benchmarks:

• Three-digit multiplication (Arithmetic)
• Algebra word problems (OMEGA benchmark)
• Codeforces programming problems

The main results are as follows:

Model & Setting	Multiplication	Lin. Eqns.	Codeforces
Qwen2.5-(Coder)-3B-Instruct	0.791	0.440	0.320
+ self-play (SQLM)	0.948	0.600	0.391
+ self-play (format reward)	0.826	0.553	N/A

SQLM yields 14% absolute improvement on arithmetic, 16% on algebra, and 7% on coding over the base model, all without any external data. The format reward baseline, which only enforces output formatting, yields much smaller gains, confirming that SQLM's improvements are due to enhanced reasoning rather than superficial answer formatting.

Qualitative Analysis

As training progresses, the proposer generates increasingly complex and diverse problems, and the solver correspondingly improves its reasoning abilities. For example, in the arithmetic task, the proposer evolves from generating simple addition/subtraction to multi-step expressions involving parentheses and exponents.

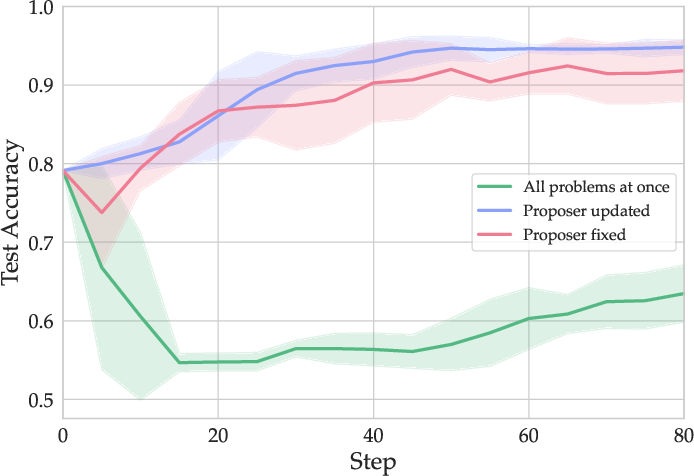
Figure 2: Comparison of generating all problems at once (pre-generation) versus incrementally via the proposer; incremental generation maintains higher data diversity and supports better learning.

Ablation studies on proposer update frequency reveal that updating every 5 or 10 steps yields the best trade-off between curriculum adaptation and solver progress, with lower variance across runs.

Data Diversity

A critical finding is that generating problems incrementally via the proposer (with frequent updates) maintains higher diversity in the training data compared to pre-generating a static dataset. PCA analysis of the generated problems confirms that online self-play produces a broader distribution of problem types and difficulties, which is essential for robust self-improvement.

Limitations

While SQLM eliminates the need for curated datasets, it does not fully remove hand-engineering. Prompt design and iteration remain necessary to constrain the generation space and ensure output format consistency, especially in code generation. The absence of external verifiers or ground-truth labels means that systematic errors can be reinforced if the model converges on internally consistent but incorrect solutions. There is also no explicit mechanism to filter for safety, relevance, or interest in the generated questions, which could be addressed in future work via meta-learning or LLM-based filtering.

Theoretical and Practical Implications

SQLM demonstrates that LLMs can serve as both data generators and solvers, enabling a closed-loop, self-improving training regime. This challenges the prevailing paradigm that post-training must rely on human-curated datasets and opens the door to scalable, autonomous model refinement. The asymmetric self-play framework provides a principled mechanism for curriculum generation and adaptive exploration in the language domain, analogous to its success in RL for robotics.

Practically, SQLM reduces the cost and effort of dataset curation, making it feasible to continually improve LLMs in domains where labeled data is scarce or expensive. The approach is model-agnostic and generalizes across tasks (arithmetic, algebra, code), as shown by successful application to both Qwen and Llama models.

Future Directions

Key avenues for future research include:

• Automated prompt evolution: Meta-learning or RL to optimize prompts and reduce manual intervention.
• Semi-supervised integration: Combining self-play with small amounts of labeled data to correct systematic errors.
• Safety and relevance filtering: LLM-based or external mechanisms to ensure generated questions are appropriate and useful.
• Scaling to larger models and more complex domains: Extending SQLM to open-ended reasoning, multi-modal tasks, or real-world applications.

Conclusion

Self-Questioning LLMs introduce a fully self-supervised, asymmetric self-play framework for LLM post-training, enabling models to autonomously generate and solve their own problems. This approach yields substantial improvements in reasoning ability across arithmetic, algebra, and code tasks, without any curated data. SQLM reframes LLMs as active agents in their own training, with significant implications for the autonomy and scalability of future AI systems.