Learning to Think: Information-Theoretic Reinforcement Fine-Tuning for LLMs (2505.10425v3)

Abstract: LLMs excel at complex tasks thanks to advances in their reasoning abilities. However, existing methods overlook the trade-off between reasoning effectiveness and efficiency, often encouraging unnecessarily long reasoning chains and wasting tokens. To address this, we propose Learning to Think (L2T), an information-theoretic reinforcement fine-tuning framework for LLMs to make the models achieve optimal reasoning with fewer tokens. Specifically, L2T treats each query-response interaction as a hierarchical session of multiple episodes and proposes a universal dense process reward, i.e., quantifies the episode-wise information gain in parameters, requiring no extra annotations or task-specific evaluators. We propose a method to quickly estimate this reward based on PAC-Bayes bounds and the Fisher information matrix. Theoretical analyses show that it significantly reduces computational complexity with high estimation accuracy. By immediately rewarding each episode's contribution and penalizing excessive updates, L2T optimizes the model via reinforcement learning to maximize the use of each episode and achieve effective updates. Empirical results on various reasoning benchmarks and base models demonstrate the advantage of L2T across different tasks, boosting both reasoning effectiveness and efficiency.

• The paper introduces a novel dense process reward mechanism that balances reasoning quality and token efficiency.
• It reformulates LLM optimization as an episodic reinforcement learning task using information gain and compression penalties.
• Empirical results show up to 3.7% accuracy improvements while reducing token usage by nearly 50%.

Learning to Think: Information-Theoretic Reinforcement Fine-Tuning for LLMs

Introduction

The paper "Learning to Think: Information-Theoretic Reinforcement Fine-Tuning for LLMs" introduces a novel approach called Learning to Think (L2T) for optimizing LLMs by balancing reasoning effectiveness and efficiency. L2T uses an information-theoretic reinforcement fine-tuning framework with a universal dense process reward, promoting optimal reasoning with fewer tokens.

Key Concepts

Information-Theoretic Dense Process Reward

The core innovation is the introduction of a dense process reward based on information-theoretic principles, which consists of two main components:

1. Fitting Information Gain: Quantifies the episode-wise information gain in model parameters, promoting updates crucial for correctness.
2. Parameter Compression Penalty: Discourages excessive updates by penalizing redundant information capture, thus preserving token efficiency.

These components drive the model to focus on meaningful reasoning steps, avoiding unnecessary token consumption.

Problem Reformulation

The problem is reformulated as an episodic reinforcement learning (RL) task. Each query-response interaction is treated as a hierarchical session of multiple episodes, allowing for process rewards to be applied at each reasoning step. These rewards guide the model by quantifying the contribution of each episode towards the final answer's accuracy.

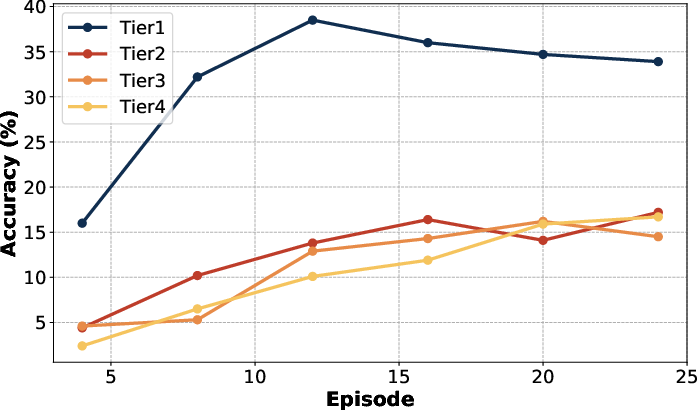
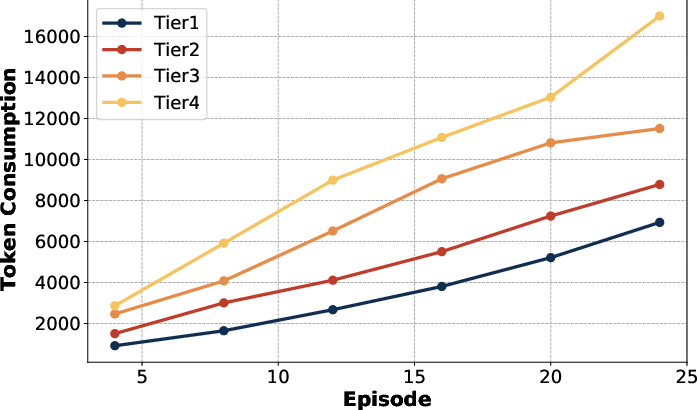
Figure 1: Results of DeepScaleR-1.5B-Preview across different tasks on Omni-MATH. We partition the generated reasoning chain into episodes, measuring accuracy $\mathrm{Acc}(k)$ and average token consumption $\overline{T}(k)$ at different episode depths.

Implementation Details

Model Training

L2T is implemented using existing LLM architectures enhanced by an RL-based optimization procedure. The dense process reward is approximated using PAC-Bayes bounds and the Fisher information matrix, significantly reducing computational complexity. The policy is trained to maximize cumulative rewards across episodes using this efficient approximation.

Code and Pseudocode

The integration with existing RL methods like GRPO is straightforward, with adaptations for episodic rewards and efficient parameter updates. The method leverages advantages from process rewards by using log-probability surprises for token-level credit assignment.

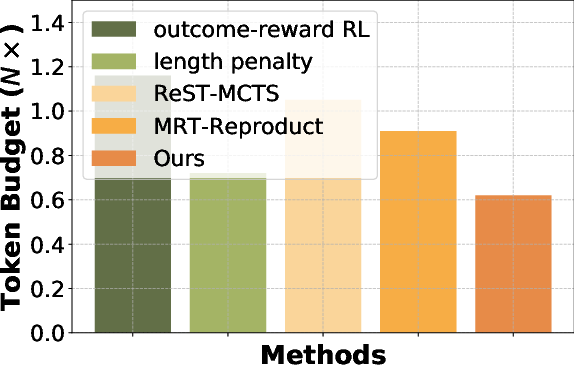
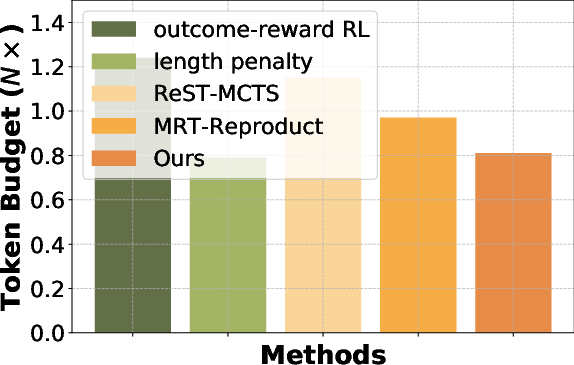
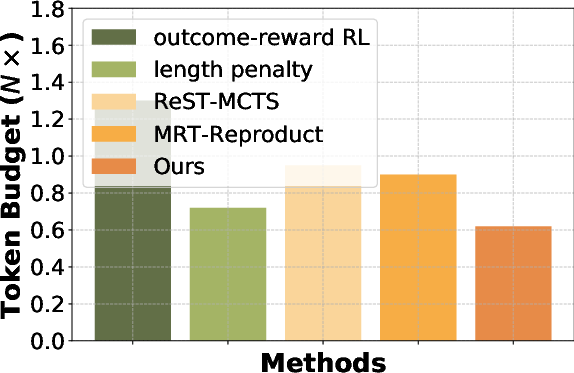
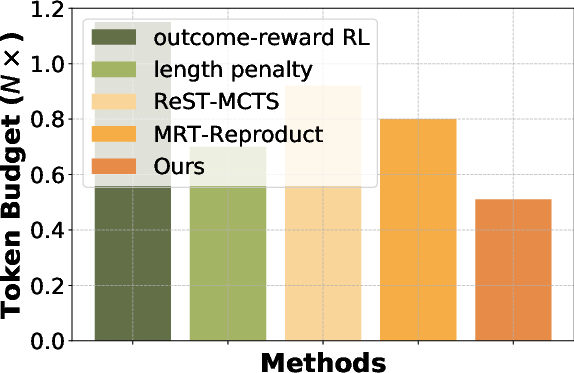
Figure 2: Efficiency comparison across different benchmarks. We compute the token budget required for each benchmark and treat the budget of the base model w/o fine-tuning as reference (1\times).

Empirical Results

Empirical results show that L2T achieves state-of-the-art performance across several reasoning benchmarks (e.g., AIME, AMC, MATH, Omni-MATH), demonstrating significant improvements in both effectiveness and efficiency. L2T outperforms traditional sparse outcome-reward strategies and other process-reward methods, achieving up to 3.7% improvements in accuracy while reducing token usage by approximately 50%.

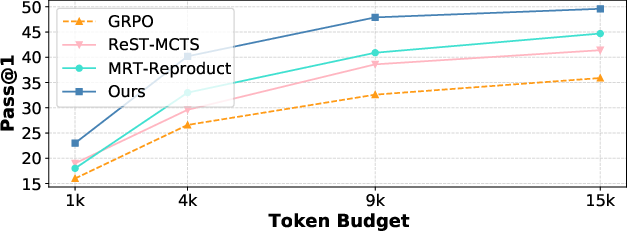
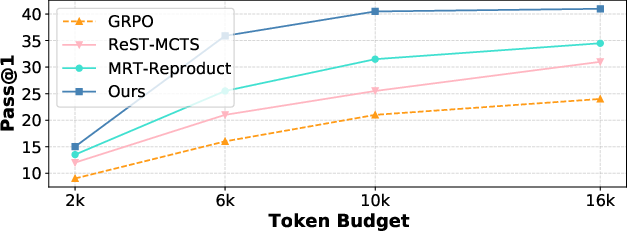
Figure 3: Pass@1 vs. token budget of different methods on AIME. We record the model reasoning accuracy under different maximum token budgets to evaluate the ability of using test-time compute.

Ablation Studies

Ablation studies confirm the critical role of both the information-theoretic dense process reward and the parameter compression penalty. The studies validate that replacing or removing these components degrades performance and increases token consumption.

Figure 4: Effect of L2T components.

Conclusion

The L2T framework presents a robust solution for enhancing LLMs, focusing on reasoning efficiency and effectiveness. By introducing an information-theoretic approach to process rewards, it offers a task-agnostic, scalable, and efficient methodology applicable across diverse reasoning tasks, marking a significant step forward in optimizing LLMs for real-world applications.