FCOC: A Fractal-Chaotic Co-driven Framework for Financial Volatility Forecasting (2511.10365v1)

Abstract: This paper introduces the Fractal-Chaotic Oscillation Co-driven (FCOC) framework, a novel paradigm for financial volatility forecasting that systematically resolves the dual challenges of feature fidelity and model responsiveness. FCOC synergizes two core innovations: our novel Fractal Feature Corrector (FFC), engineered to extract high-fidelity fractal signals, and a bio-inspired Chaotic Oscillation Component (COC) that replaces static activations with a dynamic processing system. Empirically validated on the S&P 500 and DJI, the FCOC framework demonstrates profound and generalizable impact. The framework fundamentally transforms the performance of previously underperforming architectures, such as the Transformer, while achieving substantial improvements in key risk-sensitive metrics for state-of-the-art models like Mamba. These results establish a powerful co-driven approach, where models are guided by superior theoretical features and powered by dynamic internal processors, setting a new benchmark for risk-aware forecasting.

• The paper introduces the FCOC framework, merging fractal feature correction with chaotic oscillation to enhance forecasting accuracy.
• It employs the Fractal Feature Corrector for high-fidelity signal extraction using overlapping segmentation and trend discrimination.
• Empirical tests on S&P 500 and DJI demonstrate superior performance over benchmarks using key metrics like MAE and MSE.

FCOC: A Fractal-Chaotic Co-driven Framework for Financial Volatility Forecasting

The paper presents the Fractal-Chaotic Oscillation Co-driven (FCOC) framework as a new approach to volatility forecasting in financial markets. By tackling the intertwined challenges of feature fidelity and model responsiveness, the FCOC seeks to improve the forecasting accuracy of dynamic systems such as the stock market. Its primary innovations include the Fractal Feature Corrector (FFC) for extracting high-fidelity market signals and the Chaotic Oscillation Component (COC), which enhances model responsiveness through dynamic processors.

Introduction

Financial market volatility forecasting is crucial for risk management, option pricing, and portfolio allocation. Despite their potential, standard deep learning approaches struggle with feature fidelity and model responsiveness. The Fractal Market Hypothesis and econophysics suggest that market signals are multifractal and exhibit cross-asset risk transmissions. Static activation functions, like ReLU, reveal limitations in processing chaotic financial signals due to their static nature. The paper addresses these challenges by combining chaos theory and fractal analysis.

Methodology: Fractal Feature Corrector (FFC)

The FFC improves feature fidelity using the OSW-MF-ADCCA algorithm to extract high-fidelity fractal signals. This process captures asymmetric and multifractal cross-correlations. Utilizing overlapping segmentation enhances measurement stability and reduces noise. Key steps include:

1. Profile Construction: Cumulative deviation profiles are generated from time series data.
2. Overlapping Segmentation: This involves sliding window techniques to partition profiles into segments.
3. Trend Discrimination: Local trends are identified and processed to capture financial signal dynamics.
4. Directional Fluctuation Functions: These functions are computed to analyze power-law cross-correlations.
5. Estimation of Generalized Hurst Exponents: Determines if signals obey long-range cross-correlation patterns.

   Figure 1: Conceptual Architecture of the FCOC Framework.

Methodology: Chaotic Oscillation Component (COC)

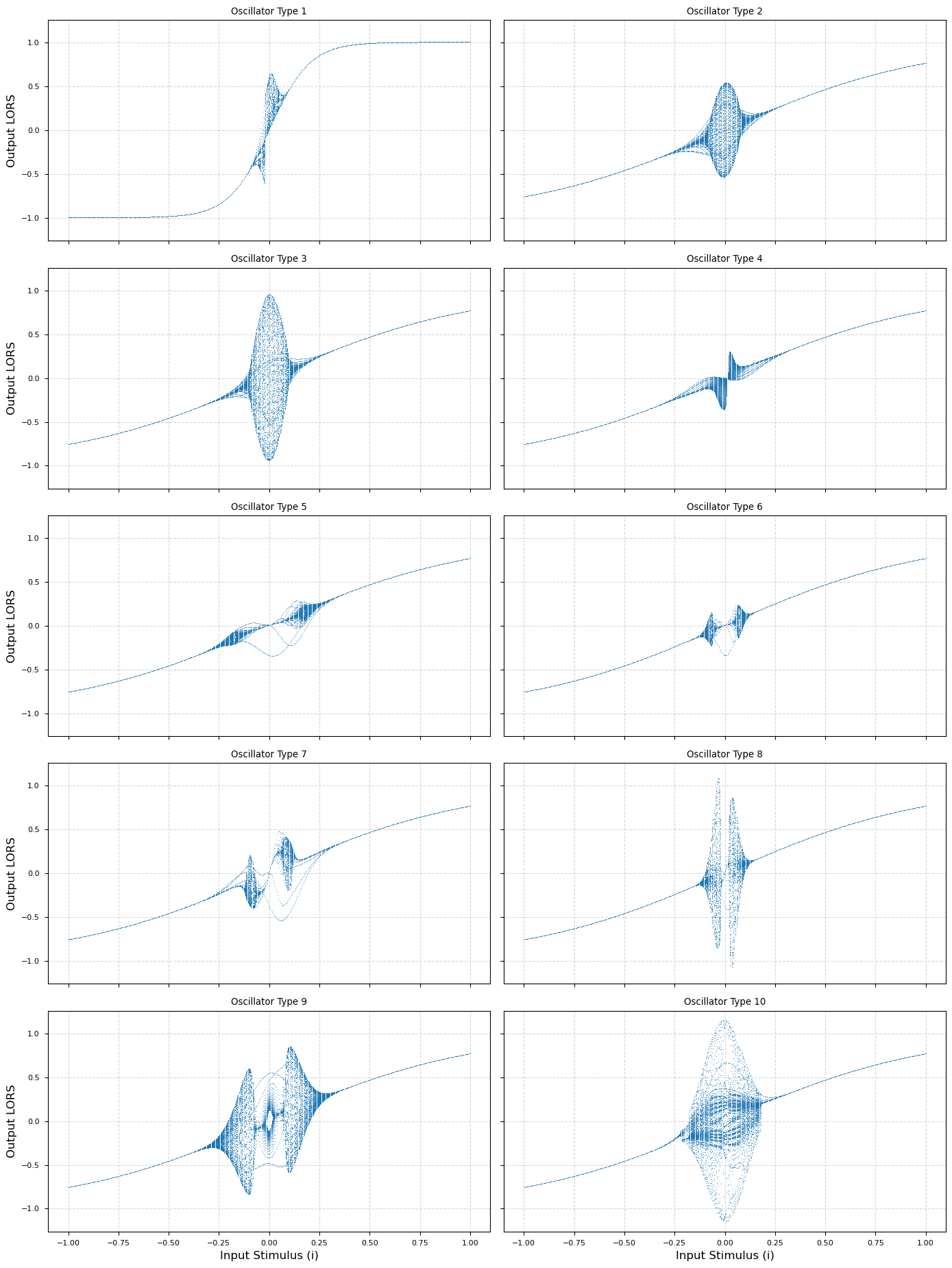
The COC replaces static activation functions with dynamic Lee oscillators exhibiting chaotic behavior. These oscillators model the non-linear dynamics of financial markets more effectively. By using retrograde signaling and dynamic meta-activation functions, the COC enables models to adapt better to volatile market conditions.

• Lee Oscillator with Retrograde Signaling: Provides a biologically-inspired dynamic system.
• Meta-Activation Library: Distills oscillator dynamics into static functions using Max-over-Time pooling.
• Maximum Response Selection: Adopts a Winner-Takes-All strategy for activation output.

  Figure 2: Neural architecture of the Lee Oscillator with Retrograde Signaling (LORS).

Empirical Analysis

The framework was validated using S&P 500 and DJI data, demonstrating substantial improvements in forecasting accuracy. Models augmented with the OSW-MF-ADCCA derived features consistently outperformed benchmarks, revealing the superiority of high-fidelity fractal signals.

• Performance Metrics: Comparative evaluations using R², QLIKE, MAE, and MSE showed enhanced results for both indices.
• Synergistic Effects: The FCOC yielded the best performance, particularly with architectures like Mamba, confirming the benefits of combining fractal feature extraction with dynamic internal processing.

  Figure 3: Bifurcation diagrams for the ten LORS types, showcasing the diverse dynamic behaviors.

Conclusion

The FCOC framework addresses fundamental limitations in financial volatility forecasting by harnessing the co-driven synergy of fractal analysis and chaotic dynamics. This approach not only improves model performance on traditional indices but also opens avenues for further research in different financial environments, like cryptocurrency markets and algorithmic trading.

Overall, the framework's robust design principles mark a significant step forward toward more accurate and dynamic financial forecasting, suggesting potential for its application in broader economic and financial contexts. Future work could focus on integrating these dynamic systems into diverse financial instruments and exploring their efficacy under extreme market conditions.

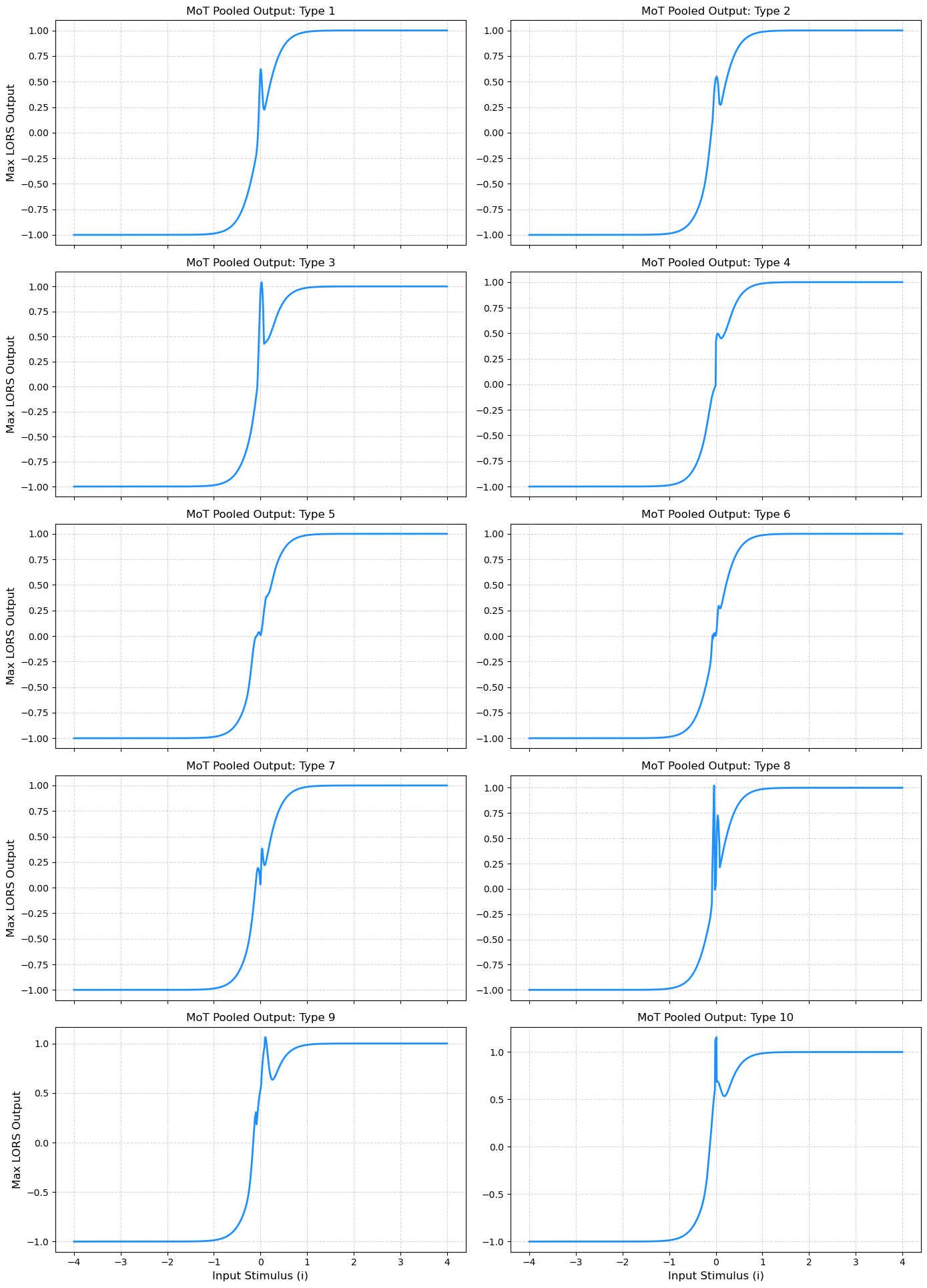
Figure 4: The ten distinct meta-activation functions, $f_{\text{type}(x)$.