Adaptive Training of INRs via Pruning and Densification (2510.23943v1)

Abstract: Encoding input coordinates with sinusoidal functions into multilayer perceptrons (MLPs) has proven effective for implicit neural representations (INRs) of low-dimensional signals, enabling the modeling of high-frequency details. However, selecting appropriate input frequencies and architectures while managing parameter redundancy remains an open challenge, often addressed through heuristics and heavy hyperparameter optimization schemes. In this paper, we introduce AIRe ($\textbf{A}$daptive $\textbf{I}$mplicit neural $\textbf{Re}$presentation), an adaptive training scheme that refines the INR architecture over the course of optimization. Our method uses a neuron pruning mechanism to avoid redundancy and input frequency densification to improve representation capacity, leading to an improved trade-off between network size and reconstruction quality. For pruning, we first identify less-contributory neurons and apply a targeted weight decay to transfer their information to the remaining neurons, followed by structured pruning. Next, the densification stage adds input frequencies to spectrum regions where the signal underfits, expanding the representational basis. Through experiments on images and SDFs, we show that AIRe reduces model size while preserving, or even improving, reconstruction quality. Code and pretrained models will be released for public use.

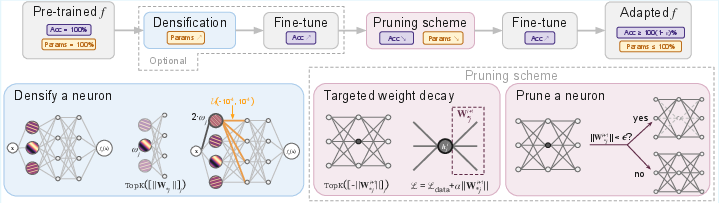
• The paper introduces AIRe, a framework that adaptively prunes low-impact neurons and densifies input frequencies to optimize INR architecture.
• It achieves significant parameter reductions (up to 60%) with only minimal loss in reconstruction quality, as evidenced by PSNR and Chamfer Distance metrics.
• The approach uses targeted weight decay and theoretical guarantees to ensure output stability and efficient training, outperforming standard pruning methods.

Adaptive Training of Implicit Neural Representations via Pruning and Densification

Introduction

Implicit Neural Representations (INRs), specifically those employing sinusoidal MLPs, are an established paradigm for encoding low-dimensional signals (e.g., images, signed distance functions, NeRFs) as continuous neural functions. Despite substantial progress, selecting appropriate input frequencies and network architectures remains ad hoc, often incurring excessive parameterization and hyperparameter tuning. The paper "Adaptive Training of INRs via Pruning and Densification" (2510.23943) presents AIRe: a robust, theoretically justified framework that adaptively optimizes INR architecture via integrated pruning and frequency densification, mitigating redundancy while improving fidelity and training stability.

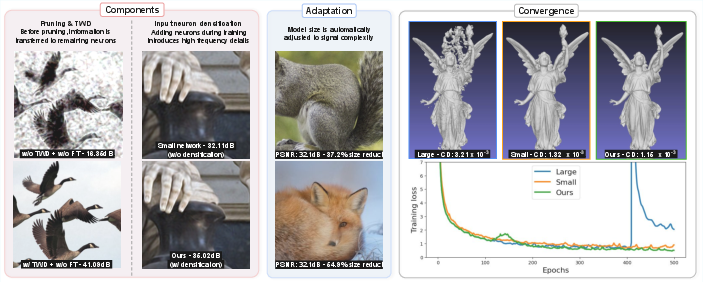
Figure 1: Schematic summarizing AIRe’s bidirectional adaptive training, demonstrating parameter reduction via pruning (birds), detail enhancement via densification (hand), and improved convergence over standard large/small models (statue).

Methodology

Network Dynamics, Pruning, and Densification

AIRe operates by iteratively modifying network structure during training. The core components include:

• Magnitude-Based Pruning: Identifies neurons with minimal contribution (via $\ell_1$ norm of outgoing weights) and schedules their removal. Theoretical analysis (Theorem 2) establishes that such pruning induces only bounded perturbations in network output, guaranteeing output stability proportional to the norm of pruned parameters and downstream weights.
• Targeted Weight Decay (TWD): A regularization term penalizes weights of neurons marked for pruning, encouraging redundancy transfer to remaining units pre-removal. Empirical and ablation analyses confirm TWD's superiority over standard weight decay, substantially reducing the need for fine-tuning.
• Input Frequency Densification: AIRe dynamically analyzes hidden layer amplitude contributions (Thrm 1, Bessel expansion), selects influential input frequencies, and expands the basis by introducing harmonics ($2 \cdot \omega_j$) in spectral regions showing underfitting. Initializations ensure stability; subsequent fine-tuning adapts the network to the expanded spectrum.

  Figure 2: AIRe pipeline: spectrum-aware densification augments input; magnitude-based pruning identifies/removes low-impact neurons, with TWD facilitating efficient information transfer.

Experimental Evaluation

AIRe is evaluated on tasks spanning image fitting (DIV2K), SDF-based 3D reconstruction (Stanford 3D Scanning Repository), and novel view synthesis (NeRF Synthetic dataset). Architectures include SIREN and FINER variants; metrics comprise PSNR, Chamfer Distance, and network parameter count. Key findings:

• Accuracy–Efficiency Trade-off: AIRe achieves dramatic reductions in network size (down to $\sim$16–36% of original parameters), while maintaining or improving reconstruction quality (e.g., PSNR drops ≤2.1% for 72% pruning, Chamfer distances on SDFs comparable or superior to large models).
• Training Stability: In SDF tasks, standard large SIRENs frequently diverge in high-frequency regimes, whereas AIRe reliably yields cleaner reconstructions, even in severely reduced networks.

  Figure 3: Armadillo/Buddha/Lucy SDF reconstructions—AIRe small models outperform direct small-network training, minimizing deviation from ground truth.

  

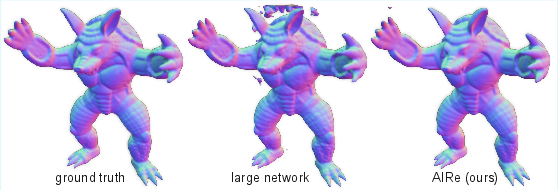
  Figure 4: Armadillo—AIRe mitigates divergence induced by overparameterization, producing artifact-free reconstructions versus noisy outputs from naïve training.

• Comparative Baselines: AIRe surpasses generic pruning methods (RigL, DepGraph) in image representation, delivering higher PSNR/SSIM even at matched pruning rates.

Ablation Studies

Detailed ablations dissect effects of:

• TWD Regularization: Pruning with TWD preserves nearly all accuracy post-removal; standard weight decay or no regularization incurs substantial quality loss. Fine-tuning remains optional at lower pruning rates with TWD.

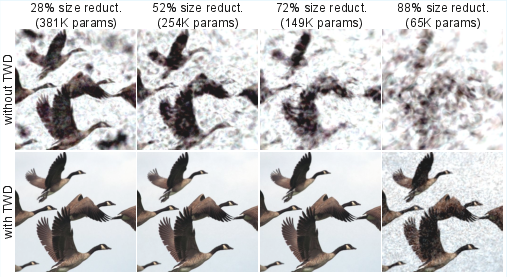
  Figure 5: Visual and quantitative (PSNR) comparison—TWD is essential for high-fidelity performance after aggressive pruning.

• Densification Schedules: Early addition of input frequencies, as well as pruning after densification, maximizes detail retention and convergence.

  Figure 6: Error maps—densify-then-prune schedule achieves best preservation of high-frequency signal, outperforming alternative pipeline orderings.

• Layerwise Pruning Analysis: Pruning first hidden layer is more robust for SIREN/FINER, supporting up to 60% parameter reduction with minor accuracy degradation.

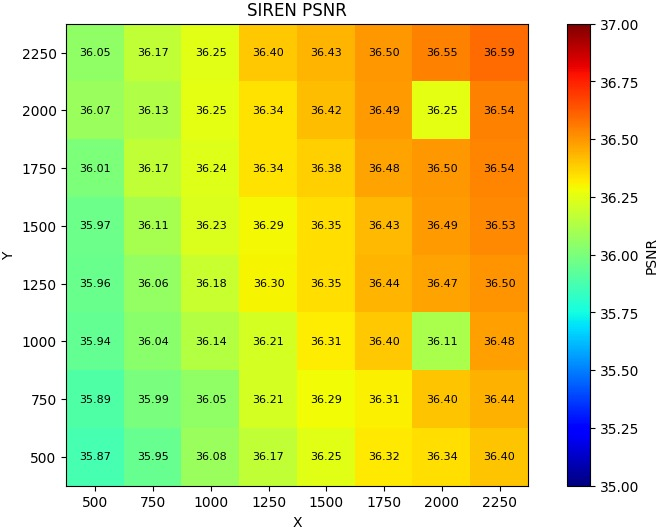
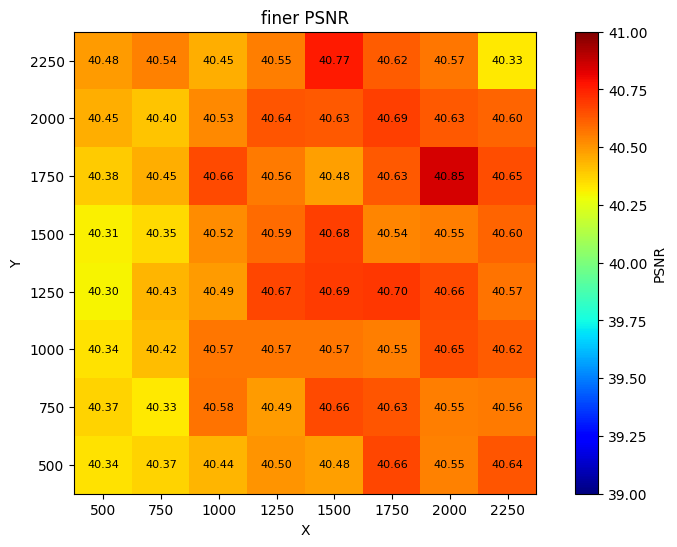
Figure 7: Epoch allocation for TWD vs fine-tuning—SIREN models benefit from increased TWD; FINER models exhibit weaker sensitivity.

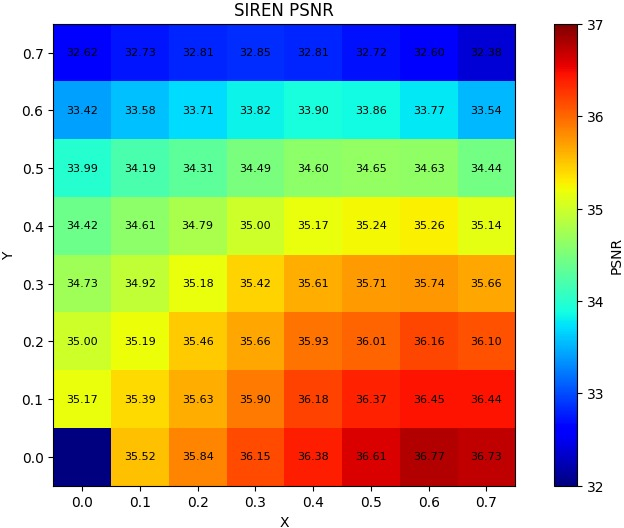
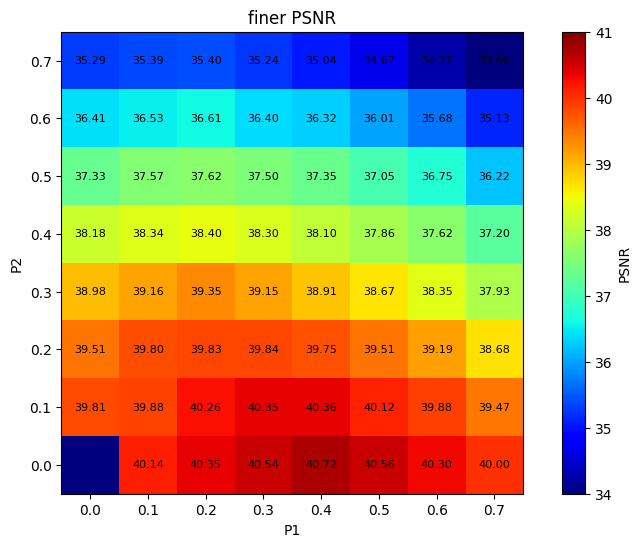
Figure 8: PSNR retention is maximized by pruning the first hidden layer compared to deeper layers.

Figure 9: Early densification and increased input neurons yield maximal PSNR.

Qualitative Comparisons & Domain Extensions

Visualizations demonstrate AIRe consistently produces reconstructions closer to ground truth and with fewer artifacts across a spectrum of geometric models (Dragon, Bunny) and NeRF scenes.

Figure 10: Dragon/Bunny SDFs—AIRe reconstructions display lower error magnitudes than size-matched small network counterparts.

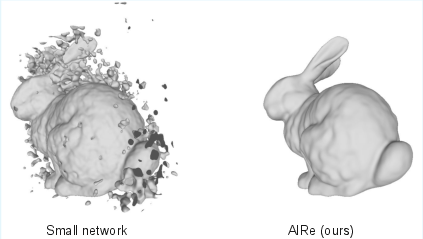
Figure 11: FINER–Bunny: AIRe eliminates artifacts prevalent in directly trained small networks.

AIRe extends efficiently to NeRF density/color network pruning, saving over 20% parameters with marginal (<$1\%$) PSNR reduction, and yielding sharper renderings compared to standard small networks.

Theoretical Implications

AIRe’s harmonically motivated densification and stability-provable pruning underpin a principled architecture search strategy for INRs. The adaptive expansion of frequency bases and judicious reduction of hidden units provides a data-dependent route to optimal spectral coverage and parameter efficiency, obviating brute-force hyperparameter grid searching and facilitating rapid convergence.

Practical Implications and Future Directions

AIRe’s parameter savings and training stability are directly relevant to INR deployment in resource-constrained environments (e.g., mobile devices, edge computing for real-time shape encoding or view synthesis) and frequency-rich domains. The TWD framework in particular suggests a generalizable regularization strategy for pruning beyond INR models, offering potential application to high-frequency task regimes.

Future expansions might incorporate dynamic adaptation for INR architectures in other modalities (temporal signals, multimodal fields), integration with meta-learning for rapid cross-task adaptation, and formulation of spectral-aware growth/prune strategies for more complex neural field architectures.

Conclusion

The AIRe framework constitutes a robust, mathematically substantiated approach to adaptive INR training, harnessing pruning and input frequency densification for compact, high-fidelity signal representation. Its empirical superiority over static and prior adaptive baselines, combined with theoretical guarantees of stability, position it as a flexible tool for efficient neural signal modeling. Future research should explore generalized adaptive strategies, more advanced information transfer mechanisms during pruning, and broader architectural extensions.