FM-SIREN & FM-FINER: Nyquist-Informed Frequency Multiplier for Implicit Neural Representation with Periodic Activation (2509.23438v2)

Abstract: Existing periodic activation-based implicit neural representation (INR) networks, such as SIREN and FINER, suffer from hidden feature redundancy, where neurons within a layer capture overlapping frequency components due to the use of a fixed frequency multiplier. This redundancy limits the expressive capacity of multilayer perceptrons (MLPs). Drawing inspiration from classical signal processing methods such as the Discrete Sine Transform (DST), we propose FM-SIREN and FM-FINER, which assign Nyquist-informed, neuron-specific frequency multipliers to periodic activations. Unlike existing approaches, our design introduces frequency diversity without requiring hyperparameter tuning or additional network depth. This simple yet principled modification reduces the redundancy of features by nearly 50% and consistently improves signal reconstruction across diverse INR tasks, including fitting 1D audio, 2D image and 3D shape, and synthesis of neural radiance fields (NeRF), outperforming their baseline counterparts while maintaining efficiency.

• The paper introduces neuron-specific, Nyquist-informed frequency multipliers to reduce redundancy and boost spectral capacity in INR architectures.
• It employs a principled design, achieving nearly orthogonal hidden activations and lowering the Frobenius norm of covariance by about 50% compared to baselines.
• Empirical results show significant improvements in audio, image, 3D shape, and NeRF tasks, reducing MSE and increasing PSNR while cutting training time.

Nyquist-Informed Frequency Diversity in Periodic Activation INRs: FM-SIREN & FM-FINER

Introduction and Motivation

Implicit Neural Representations (INRs) employing periodic activation functions such as SIREN and FINER have become central to signal and scene modeling tasks. However, prior INR architectures suffer from hidden feature redundancy, originating from the assignment of a fixed frequency multiplier to all neurons within a layer. This design choice induces strong frequency bias and correlated hidden embeddings, inherently constraining the expressive (spectral) capacity, especially for high-fidelity regression and reconstruction. This paper proposes FM-SIREN and FM-FINER, introducing neuron-specific, Nyquist-informed frequency multipliers to periodic activations, with theoretical grounding in classical signal processing—specifically, the orthogonality and completeness guarantees of transforms like the Discrete Sine Transform (DST).

Methodological Contributions

FM-SIREN and FM-FINER utilize a Nyquist-derived, layer-local assignment of frequency multipliers. For each neuron, the activation operates at a distinct frequency within the Nyquist-limited bandwidth, matching the effective spectral range permissible by the sampling theorem. For FM-FINER, the frequency span is further adjusted (by a factor of 2/3) to accommodate the broader baseband of chirp activations, optimally reducing aliasing artifacts. This principled design obviates the need for manual hyperparameter tuning and increases frequency diversity at a fundamental network architectural level.

Theoretical analysis reveals that conventional periodic INRs apply identical activations per layer, yielding correlated feature vectors and substantial covariance in hidden activations. FM-SIREN and FM-FINER yield nearly orthogonal embeddings, evidenced by a reduction of the Frobenius norm of the covariance matrix by approximately 50%. The architecture thus closes the gap in linear representational capacity between INR MLPs and classical explicit bases like DST.

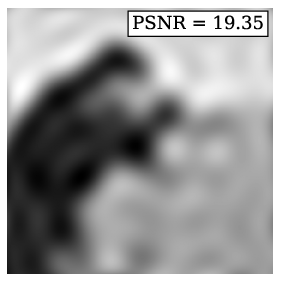
Figure 1: 2D cameraman image reconstructions—FM-SIREN and FM-FINER outperform SIREN, FINER, and DST in PSNR with single-layer networks.

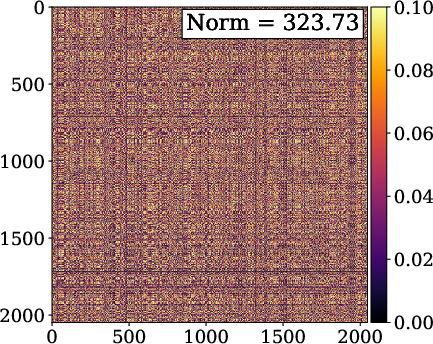
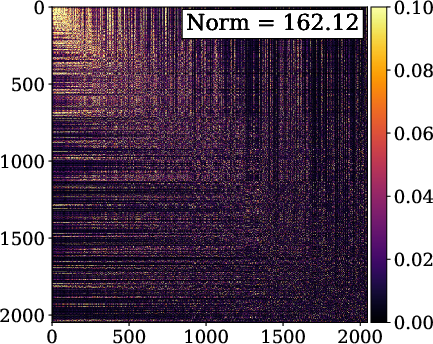
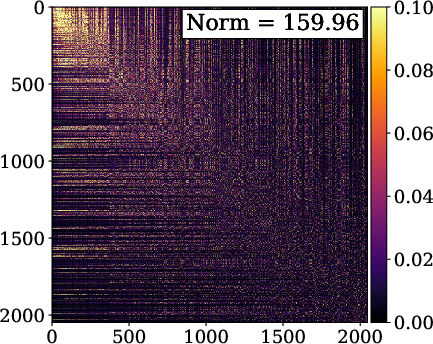
Figure 2: INR-based reconstructions showing superior performance and compactness of FM-SIREN relative to SIREN with fixed frequency multipliers.

Empirical Results and Quantitative Analysis

Audio Fitting

On the Spoken English Wikipedia dataset, FM-SIREN and FM-FINER demonstrate an order-of-magnitude reduction in MSE (mean squared error) compared to baselines. Models were trained with $f_s = 4$kHz (Nyquist frequency: 2kHz) and two hidden layers of 256 neurons.

• FM-FINER: $4.055 \times 10^{-5}$ MSE (best)
• FM-SIREN: $4.738 \times 10^{-5}$ MSE (second best)
• Baselines: Higher MSE by at least one decimal order.

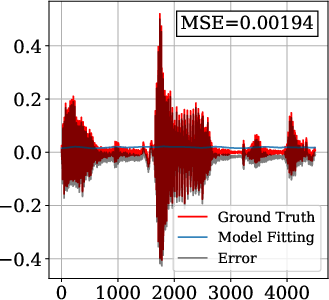
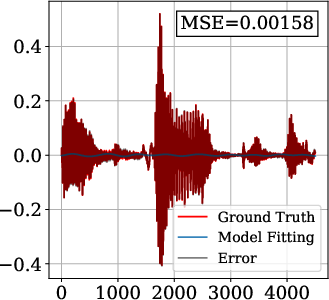
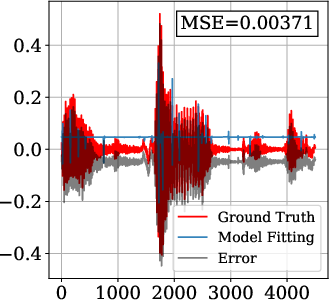
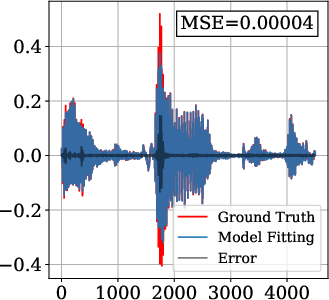
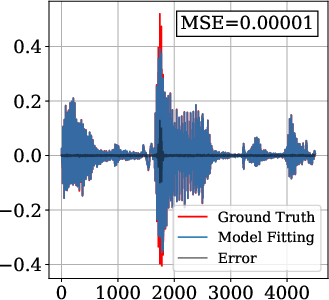
Figure 3: Audio signal reconstruction—FM-SIREN and FM-FINER capture high-frequency details unattainable by baseline periodic INRs.

Image Fitting

Evaluations performed on the Kodak and BSDS500 datasets confirm that FM-SIREN and FM-FINER achieve superior PSNR and SSIM scores, with two-layer networks matching or exceeding deeper baseline architectures.

• PSNR: FM-FINER achieves up to 32.475dB (Kodak), outperforming positional encoding and WIRE.
• SSIM: FM-SIREN reaches 0.874 (Kodak), significantly above classical INR baselines.

Figure 4: Image reconstruction on Philips Circle Pattern—FM-SIREN produces sharper features and reduced noise.

3D Shape Fitting

Shape reconstruction on the Stanford 3D Scanning Repository shapes yields higher Intersection over Union (IoU):

• FM-FINER achieves up to 0.996 IoU (dragon), consistently best across all tested 3D objects.
• Both FM models require no additional parameters or compute time versus SIREN/FINER.

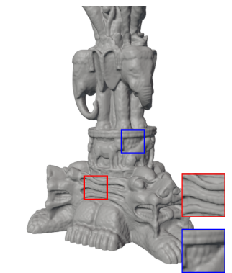
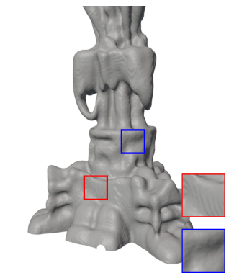
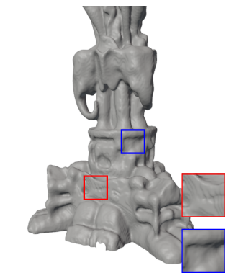
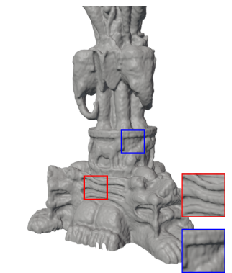
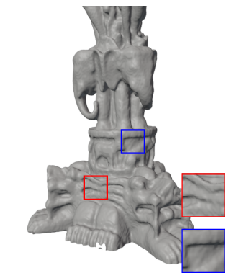
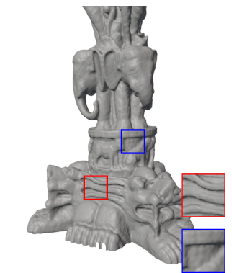
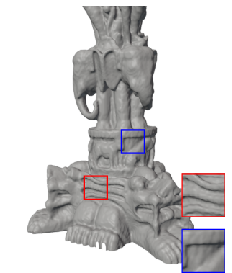
Figure 5: 3D shape fitting—FM-SIREN reconstructs fine shapes and details unmatched by competitors.

Neural Radiance Fields (NeRF)

On the Blender NeRF dataset, FM-SIREN and FM-FINER enhance PSNR while reducing training time (up to 17% less time). While quantitative improvements are modest, efficiency gains are visible, with five-layer FM-INR models exceeding positional encoding and wavelet-based INRs.

Figure 6: NeRF scene reconstruction—FM-SIREN surpasses baseline periodic INR methods in accuracy and computational cost.

Network Design Studies

Ablation studies confirm that:

• Frequency diversity surpasses gains offered by increasing width or depth.
• Saturation occurs when neuron count exceeds Nyquist resolution; excessive depth propagates high-frequency noise.
• Spectral diversity is the key determinant of improved generalization and fidelity.

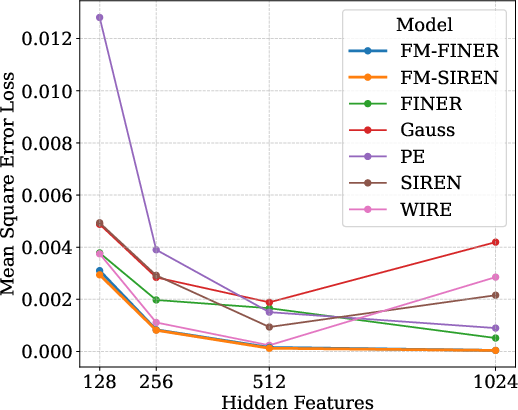
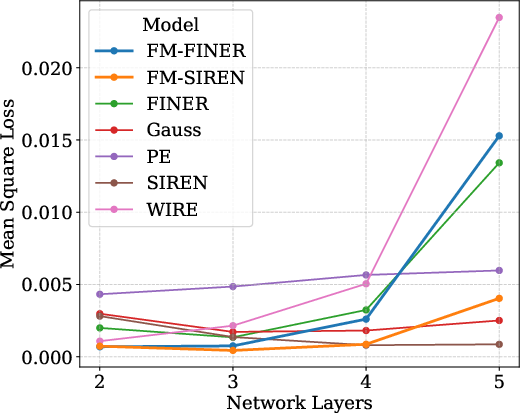
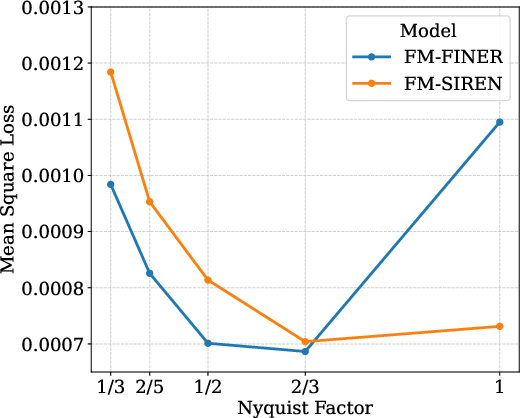
Figure 7: Network width paper—performance stagnates as redundancy increases, confirming frequency diversity as the main limiting factor.

Theoretical and Practical Implications

Inducing frequency diversity at the activation level bridges classical signal processing with neural architectures. Orthogonal neuron-wise frequency assignment enables efficient and compact representations, suggesting new paradigms for INR design:

• Network size can be reduced without loss of fidelity—two-layer FM-INRs outperform five-layer SIREN and FINER.
• Reduced training time in high-dimensional tasks (NeRF synthesis) implies practical utility for real-time or large-scale applications.
• The framework establishes potential for parameter sharing and knowledge transfer across bandwidth-adaptive tasks.

The explicit connection between classical signal orthogonality and modern MLP expressive power opens avenues for hybrid architectures that exploit analytically-derived spectra for neural networks, informing further combinations (e.g., harmonic MLPs, wavelet-based INRs, mixture-of-experts with frequency-banded activations).

Conclusion

FM-SIREN and FM-FINER demonstrate that Nyquist-informed, neuron-specific frequency multipliers control feature redundancy and promote orthogonality in hidden activations. Consistent performance gains across audio, image, 3D shape, and NeRF tasks validate the method theoretically and empirically. The implications for scalable, efficient, high-fidelity INR construction reveal opportunities for new architectures uniting classical basis principles with deep learning, and suggest further research on adaptive, data-driven frequency allocation within neural networks.