Training Neural Networks by Optimizing Neuron Positions (2506.13410v1)

Abstract: The high computational complexity and increasing parameter counts of deep neural networks pose significant challenges for deployment in resource-constrained environments, such as edge devices or real-time systems. To address this, we propose a parameter-efficient neural architecture where neurons are embedded in Euclidean space. During training, their positions are optimized and synaptic weights are determined as the inverse of the spatial distance between connected neurons. These distance-dependent wiring rules replace traditional learnable weight matrices and significantly reduce the number of parameters while introducing a biologically inspired inductive bias: connection strength decreases with spatial distance, reflecting the brain's embedding in three-dimensional space where connections tend to minimize wiring length. We validate this approach for both multi-layer perceptrons and spiking neural networks. Through a series of experiments, we demonstrate that these spatially embedded neural networks achieve a performance competitive with conventional architectures on the MNIST dataset. Additionally, the models maintain performance even at pruning rates exceeding 80% sparsity, outperforming traditional networks with the same number of parameters under similar conditions. Finally, the spatial embedding framework offers an intuitive visualization of the network structure.

• The paper introduces a novel spatial embedding approach that optimizes neuron positions to reduce parameter complexity.
• The paper employs distance-dependent synaptic weights and integrated pruning techniques to boost efficiency and scalability.
• The spatial embedding framework improves interpretability and is well-suited for deployment in resource-constrained environments.

Training Neural Networks by Optimizing Neuron Positions

Introduction

The paper "Training Neural Networks by Optimizing Neuron Positions" (2506.13410) introduces a novel approach to improving the efficiency and scalability of deep learning models. By optimizing neuron positions in Euclidean space and using distance-dependent wiring rules for synaptic weights, it proposes a biologically inspired inductive bias to reduce parameter counts, thus facilitating deployment on resource-constrained devices.

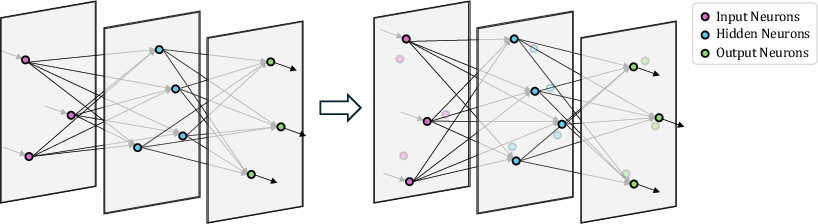
Figure 1: An illustration of a three-layer feedforward network embedded in three-dimensional Euclidean space. Neurons optimize their positions within their respective two-dimensional layers.

Methods

This research offers an innovative way to train neural networks by embedding neurons within a spatial framework, utilizing Euclidean geometry to define their positions. The synaptic weight between two neurons is inversely proportional to the distance between them, as expressed by:

$w_{ij} = \frac{1} {\|p_i - p_j\|_2}$

By fixing z-coordinates according to layer index, neurons optimize their remaining coordinates, providing a structured connectivity model (Figure 1). This design introduces efficiency in parameter handling, reducing traditional $O(n^2)$ complexity to $O(n)$, where $n$ is the number of neurons. The approach extends to Multi-layer Perceptrons (MLPs) and Spiking Neural Networks (SNNs), potentially enhancing existing architectures with additional compression technologies such as pruning.

Experiments and Results

Performance Evaluation

Experimentation on MNIST using MLPs with spatial embeddings demonstrated competitive test accuracy. Notably, a 3D MLP with 2,048 hidden neurons achieved an accuracy of 0.9217 $\pm$ 0.0024, compared to baseline MLPs with varying neuron configurations.

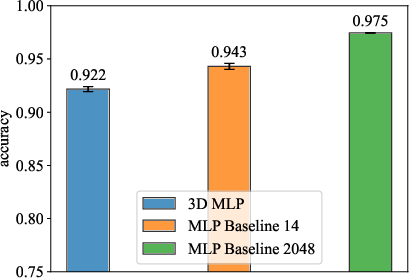
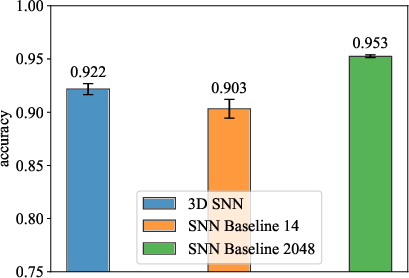
Figure 2: MLP Performance Comparison.

Similarly, spatially embedded SNNs showed promising results, outperforming some baseline models with comparable parameter counts.

Magnitude-Based Weight Pruning

Two approaches were explored to integrate pruning into spatially embedded models:

1. Post-training Pruning: Longest neuronal connections, correlating to weakest synaptic weights, were minimized (Figure 3).
2. Integrated Pruning During Training: Iterative removal of minimal weights during model development showed improvements in efficiency without compromising accuracy.

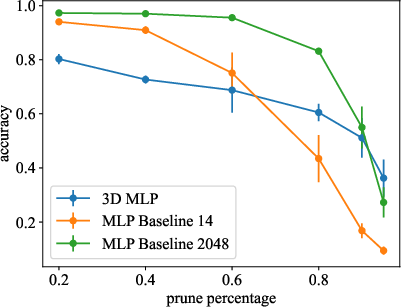
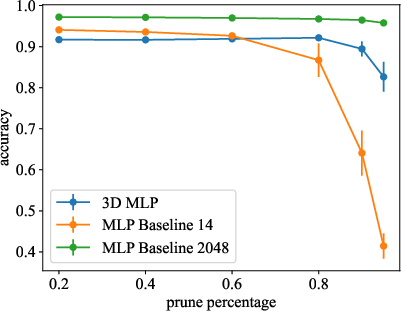
Figure 3: Models are pruned after training.

Optimizing Z-Coordinates

Relaxing fixed spatial layers and optimizing z-coordinates permitted additional flexibility. This resulted in improved performance even while maintaining feedforward layer connectivity, although still trailing specialized baseline architectures.

Discussion

The spatial embedding framework enables neural models to naturally incorporate geometric constraints into their architecture, potentially emulating biological efficiency by minimizing wiring length. Embedded models offer intuitive visual interpretations of structural and activation patterns in neural networks, aiding explainability and debugging.

Notwithstanding the potential efficiency gains, spatially embedded MLPs face challenges when compared with conventional architectures due to dependencies introduced by concurrent weight optimization. Comprehensive tasks might benefit from these constraints as a form of side channel robustness or inductive bias across extended applications.

Conclusion

This paper presents a biologically inspired method to embed neurons within three-dimensional Euclidean space to reduce parameter complexity. Notable prospects include improved design for deployment in resource and energy-constrained environments, with demonstrated robustness to pruning. Future research should expand on this model by evaluating its application across varied datasets and architectures. Potential applications might explore deeper spatial flexibility and sparseness mimicking biological long-range communication patterns. Such advancements could bridge artificial neural network design with the compactness of biological systems, showcasing spatially embedded neural networks as proficient compact AI frameworks.

In conclusion, optimizing neuron positions within Euclidean space presents a promising approach to enhancing AI model efficiency, scalability, and interpretability, laying the groundwork for future bio-inspired design advancements in machine learning.