Splat the Net: Radiance Fields with Splattable Neural Primitives (2510.08491v1)

Abstract: Radiance fields have emerged as a predominant representation for modeling 3D scene appearance. Neural formulations such as Neural Radiance Fields provide high expressivity but require costly ray marching for rendering, whereas primitive-based methods such as 3D Gaussian Splatting offer real-time efficiency through splatting, yet at the expense of representational power. Inspired by advances in both these directions, we introduce splattable neural primitives, a new volumetric representation that reconciles the expressivity of neural models with the efficiency of primitive-based splatting. Each primitive encodes a bounded neural density field parameterized by a shallow neural network. Our formulation admits an exact analytical solution for line integrals, enabling efficient computation of perspectively accurate splatting kernels. As a result, our representation supports integration along view rays without the need for costly ray marching. The primitives flexibly adapt to scene geometry and, being larger than prior analytic primitives, reduce the number required per scene. On novel-view synthesis benchmarks, our approach matches the quality and speed of 3D Gaussian Splatting while using $10\times$ fewer primitives and $6\times$ fewer parameters. These advantages arise directly from the representation itself, without reliance on complex control or adaptation frameworks. The project page is https://vcai.mpi-inf.mpg.de/projects/SplatNet/.

• The paper introduces splattable neural primitives that integrate neural radiance field expressivity with the real-time efficiency of primitive-based splatting.
• The method employs shallow MLPs to parameterize density inside ellipsoidal primitives and utilizes closed-form integration for rapid, accurate rendering with fewer primitives.
• Extensive experiments demonstrate significant reductions in memory and computation while achieving high-fidelity scene reconstructions on both synthetic and real datasets.

Splat the Net: Radiance Fields with Splattable Neural Primitives

Introduction and Motivation

The paper introduces a novel radiance field representation, termed splattable neural primitives, which unifies the expressivity of @@@@1@@@@ (NeRFs) with the real-time rendering efficiency of primitive-based splatting methods such as 3D Gaussian Splatting (3DGS). Traditional neural volumetric representations, while highly expressive, suffer from expensive ray marching during rendering. In contrast, primitive-based approaches enable efficient splatting but are limited by the analytic form and geometric rigidity of their primitives. The proposed method leverages shallow neural networks to parameterize the density field within each spatially bounded ellipsoid primitive, enabling closed-form integration along view rays and efficient splatting without sacrificing modeling flexibility.

Figure 1: (a) Overview of volumetric splattable neural primitives. Each primitive is spatially bounded by an ellipsoid, and its density is parameterized as a shallow neural network. (b) A real scene rendered using Gaussian primitives (left) and neural primitives (right). The neural primitive approach achieves comparable PSNR with fewer primitives.

Taxonomy and Positioning of Radiance Field Representations

The work situates itself at the intersection of two central design axes for radiance field representations: atomicity (monolithic vs. distributed) and neurality (non-neural vs. neural). Previous approaches either employ monolithic neural networks (e.g., NeRF) requiring ray marching, or distributed analytic primitives (e.g., 3DGS) supporting efficient splatting. The proposed splattable neural primitives are the first to combine a fully neural, distributed primitive-based representation with efficient splatting, eliminating the need for costly ray marching while retaining neural flexibility.

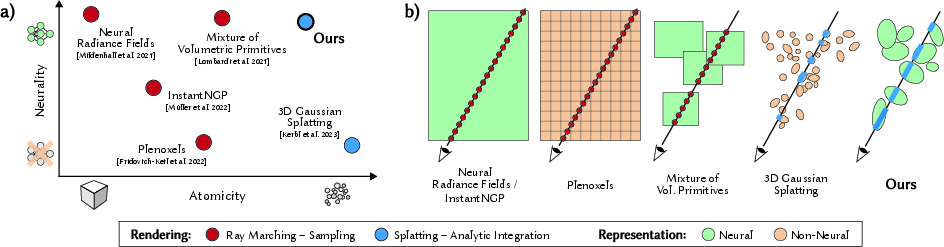
Figure 2: (a) Taxonomy of radiance field representations along atomicity and neurality axes. (b) Rendering algorithms associated with each representation. The proposed method uniquely supports neural, primitive-based splatting.

Methodology

Neural Primitive Representation

Each primitive is spatially bounded by an ellipsoid, parameterized by its center, scale, and rotation. The density field within the ellipsoid is modeled by a shallow neural network with a single hidden layer and periodic activation (cosine), normalized to the ellipsoid's domain. This architecture admits an exact analytical solution for line integrals along view rays, enabling efficient computation of the splatting kernel.

The density function is defined as:

$$\sigma(\mathbf{x}) = f_\sigma\left(\frac{\mathbf{x} - \mathbf{x}_B}{\|\mathbf{s}_B\|_\infty}\right)$$

where $f_\sigma$ is a shallow MLP with periodic activation, and the normalization ensures domain consistency.

Rendering via Closed-Form Integration

Rendering proceeds by analytically computing the entry and exit points of each view ray through the ellipsoid, followed by closed-form integration of the neural density field along the ray. The antiderivative of the density field is derived, allowing the accumulated density to be computed with only two network evaluations per primitive per ray. The splatting kernel is then:

$$\alpha(\mathbf{r}) = 1 - \exp\left(-\max(0, \hat{\alpha}(t_\text{in}, t_\text{out}, \mathbf{o}, \mathbf{d}))\right)$$

where $\hat{\alpha}$ is the closed-form integral of the density along the ray segment inside the ellipsoid.

Front-to-back compositing is performed using alpha blending of the splatting kernels, yielding perspectively accurate and efficient rendering.

Population Control and Training

Primitive population is managed via a gradient-based densification and pruning strategy, using the magnitude of network weight gradients as the criterion. Primitives with high gradients are split or duplicated, while those with low gradients are pruned. Training employs the same loss as 3DGS, with an additional geometric regularization term to penalize extreme anisotropy in primitive shapes.

Expressivity and Efficiency

The neural density field enables each primitive to represent complex, non-ellipsoidal structures, reducing the number of primitives required for high-fidelity scene reconstruction. Empirical results demonstrate that neural primitives can represent intricate geometries (e.g., teapot handles, leaf cuts) with $4\times$ fewer primitives and $16\times$ fewer parameters than Gaussian primitives.

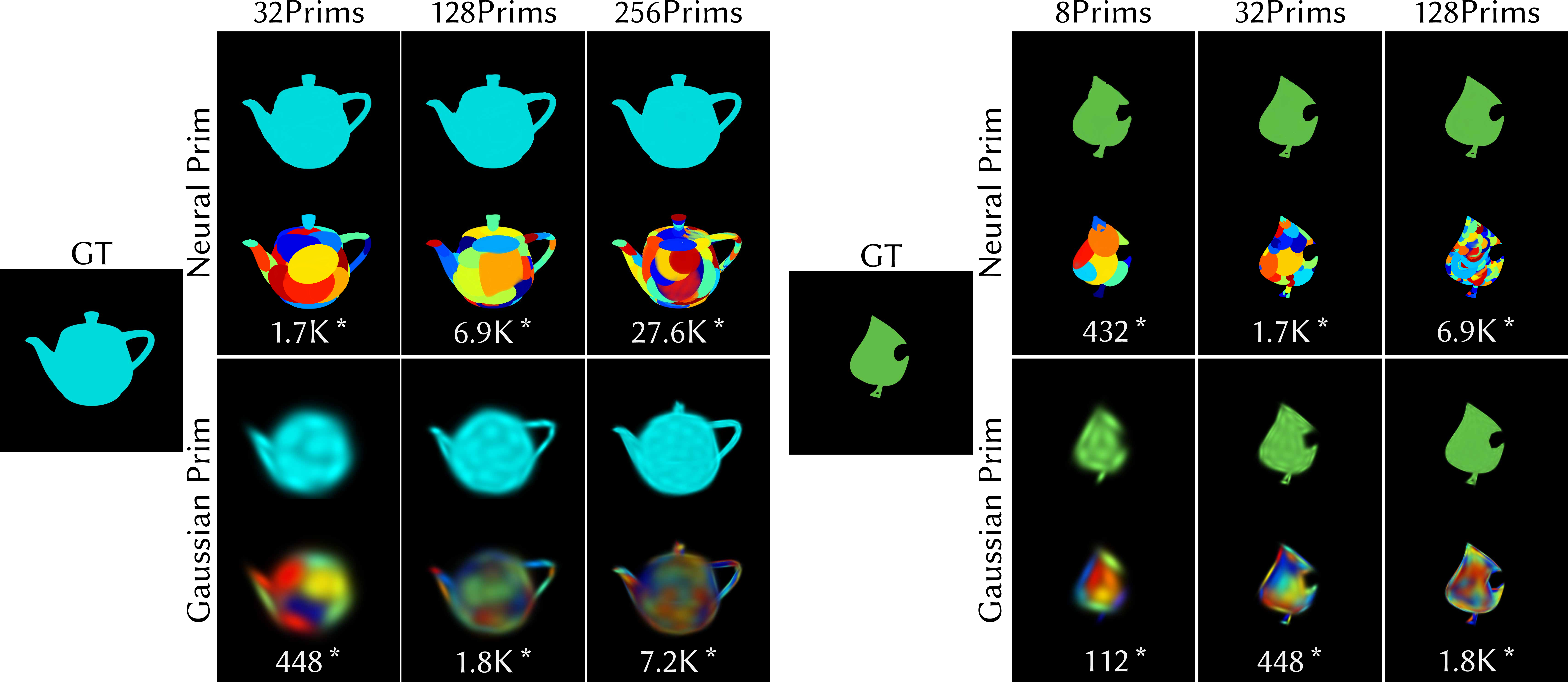
Figure 3: Expressivity comparison between neural and Gaussian primitives on teapot and leaf datasets. Neural primitives deform to represent complex structures with fewer parameters.

Quantitative and Qualitative Evaluation

Synthetic Scenes

On the Synthetic NeRF dataset, the method matches or exceeds the image quality of 3DGS under constrained memory budgets, achieving higher PSNR, SSIM, and lower LPIPS with $10\times$ fewer primitives and $6\times$ fewer parameters. Under unlimited memory, performance is comparable to 3DGS.

Real Scenes

On real datasets (Mip-NeRF360, Tanks & Temples, Deep Blending), the method achieves high-fidelity reconstructions with image quality and runtime comparable to state-of-the-art splatting-based approaches, but with substantially reduced memory usage. Compared to monolithic neural representations, rendering speed is improved by over an order of magnitude.

Ablation Studies

Ablations reveal that alternative neural integration strategies (e.g., AutoInt) induce view-dependent density and multi-view inconsistencies, whereas the proposed shallow MLP approach ensures multi-view consistency. Increasing network width and frequency multiplier enhances expressivity in toy settings, but gains diminish on real scenes due to optimization challenges. Geometric regularization stabilizes training and improves qualitative results.

Applications: Dynamic Scenes and Relighting

The neural primitive framework is readily extensible to dynamic scene representation and relighting. By augmenting the input domain of the density field with temporal or lighting parameters, the method can reconstruct volumetric dynamic scenes and synthesize relit images without requiring intrinsic properties.

Implementation Considerations

• Computational Requirements: Closed-form integration reduces per-ray computation to two network evaluations per primitive, enabling real-time rendering on commodity GPUs.
• Memory Footprint: Each neural primitive requires 99 parameters, $1.6\times$ more than a Gaussian primitive, but the reduced number of primitives yields overall lower memory usage.
• Optimization Landscape: Training millions of shallow networks is under-constrained and may suffer from local minima; geometric regularization and improved optimization strategies are recommended.
• Deployment: The method is implemented in PyTorch and CUDA, and is compatible with existing splatting-based rendering pipelines.

Implications and Future Directions

The splattable neural primitive representation bridges the gap between neural expressivity and splatting efficiency, enabling compact, high-fidelity, real-time radiance field rendering. The approach is orthogonal to advances in color field modeling and primitive densification, suggesting potential for integration with advanced control and adaptation frameworks. Future research should address optimization challenges for large-scale neural primitive populations and explore further extensions to multimodal and dynamic scene representations.

Conclusion

The paper presents a principled approach to radiance field modeling that combines the strengths of neural and primitive-based representations. By parameterizing density fields with shallow neural networks and leveraging closed-form integration, the method achieves high expressivity and real-time rendering efficiency. Empirical results validate the approach across synthetic and real datasets, with significant reductions in memory and computational requirements. The framework is extensible to dynamic and relighting tasks, and opens new avenues for efficient, flexible neural scene representations.