Fine-Tuning Masked Diffusion for Provable Self-Correction

Published 1 Oct 2025 in cs.LG | (2510.01384v1)

Abstract: A natural desideratum for generative models is self-correction--detecting and revising low-quality tokens at inference. While Masked Diffusion Models (MDMs) have emerged as a promising approach for generative modeling in discrete spaces, their capacity for self-correction remains poorly understood. Prior attempts to incorporate self-correction into MDMs either require overhauling MDM architectures/training or rely on imprecise proxies for token quality, limiting their applicability. Motivated by this, we introduce PRISM--Plug-in Remasking for Inference-time Self-correction of Masked Diffusions--a lightweight, model-agnostic approach that applies to any pretrained MDM. Theoretically, PRISM defines a self-correction loss that provably learns per-token quality scores, without RL or a verifier. These quality scores are computed in the same forward pass with MDM and used to detect low-quality tokens. Empirically, PRISM advances MDM inference across domains and scales: Sudoku; unconditional text (170M); and code with LLaDA (8B).

Abstract PDF Chat (Pro)

Summary

The paper proposes PRISM, a plug-and-play fine-tuning framework for Masked Diffusion Models that enables provable self-correction at inference time.
It leverages a lightweight adapter to learn per-token quality scores using a binary cross-entropy loss, validated across domains like Sudoku, text, and code.
Empirical results demonstrate improved success rates, generative perplexity, and sample efficiency, highlighting PRISM’s robustness and scalability.

Fine-Tuning Masked Diffusion for Provable Self-Correction: PRISM

This paper introduces PRISM, a plug-and-play fine-tuning framework for Masked Diffusion Models (MDMs) that enables provable self-correction at inference time. PRISM is designed to be model-agnostic, requiring only a lightweight adapter and fine-tuning, and is theoretically grounded to learn per-token quality scores for remasking and revision. The framework is validated across multiple domains and scales, including Sudoku, unconditional text generation, and code synthesis.

Figure 1: PRISM overview. MDMs learn an unmasking posterior to unmask tokens, which remain fixed; PRISM introduces per-token quality to detect and remask incorrect tokens, enabling self-correction during inference.

Background: Masked Diffusion Models and Self-Correction

MDMs operate by iteratively unmasking tokens in a sequence, starting from a fully masked state and sampling clean tokens from learned unmasking posteriors. The flexibility in generation order and scalability has led to strong performance in reasoning, coding, and planning tasks. However, standard MDMs lack the ability to revise early mistakes: once a token is unmasked, it remains fixed, precluding self-correction.

Prior approaches to self-correction in MDMs either rely on imprecise proxies for token quality (e.g., random remasking, confidence scores at unmasking time) or require architectural changes and retraining, limiting their practical applicability. PRISM addresses both limitations by providing a principled, efficient, and theoretically justified mechanism for per-token quality estimation and remasking.

PRISM: Theoretical Foundation and Training Pipeline

PRISM defines per-token quality as the likelihood of a token given the rest of the sequence, i.e., $g_\star^i(x) = p(x^i = x^i \mid x \oplus m_i)$ , where $x \oplus m_i$ denotes the sequence with the $i$ -th token masked. The key insight is to fine-tune an auxiliary head attached to a pretrained MDM backbone, using a binary cross-entropy loss that is provably minimized at the true per-token quality.

The training pipeline consists of two steps: (a) masking a sequence to obtain $(x, y)$ , and (b) unmasking a subset of indices in $y$ using the pretrained MDM to obtain $y'$ . The adapter head is trained to predict the per-token quality for each unmasked position, supervised by whether the sampled token matches the ground truth.

Figure 2: PRISM training pipeline. Fine-tuning samples are constructed by masking and unmasking; a lightweight adapter is added to the pretrained MDM to jointly compute unmasking posterior and per-token quality.

The adapter head shares the backbone with the unmasking head, and outputs a scalar per position via a sigmoid activation. The total loss combines the PRISM binary cross-entropy with the original MDM cross-entropy as a regularization term. Multiple $(x, y')$ pairs can be generated per batch for data efficiency, and LoRA adapters can be used for parameter-efficient fine-tuning.

Inference Procedure and Design Choices

At inference, PRISM alternates between unmasking and remasking. For each step, the model computes both the unmasking posterior and per-token quality in a single forward pass. Tokens with the lowest quality scores are selected for remasking, and new tokens are sampled for masked positions. This procedure introduces no additional computational overhead compared to vanilla MDM inference.

Design choices include the number of tokens to unmask/remask per step, selection rules for indices, and scheduling of remasking activation. For unconditional generation, diversity can be preserved by adding loop steps after initial generation, where random subsets of tokens are remasked and unmasked iteratively.

Empirical Results

Sudoku

PRISM is evaluated on a 30M-parameter DiT MDM for Sudoku. Fine-tuning with PRISM rapidly improves success rates, outperforming baselines such as ReMDM and ReMDM-conf. Visualization of per-token quality shows that PRISM reliably identifies incorrect cells, assigning low scores to misfilled positions and high scores to correct ones.

Unconditional Text Generation

A 170M-parameter DiT MDM pretrained on OpenWebText is fine-tuned with PRISM using only 1600× fewer tokens than pretraining. PRISM achieves superior generative perplexity and MAUVE scores compared to baselines, especially with fewer sampling steps. Entropy remains comparable, indicating no loss in diversity. Loop-based remasking further enhances sample quality.

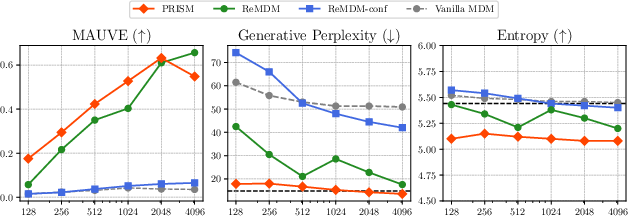
Figure 3: Assessing PRISM on unconditional text generation. PRISM (red) outperforms baselines in generative perplexity and MAUVE, particularly with fewer sampling steps.

Code Generation with LLaDA-8B

PRISM is applied to LLaDA-8B-Instruct, an 8B-parameter MDM, with a LoRA adapter and auxiliary head. Fine-tuning on 0.1M code pairs for 100 epochs yields strong performance on MBPP, outperforming baselines by 2.7% in the low-step regime. The approach is highly sample-efficient, requiring <500 GPU-hours.

Ablation Studies

Ablations on fine-tuning hyperparameters $(k, n_y)$ show that smaller $k$ (number of tokens updated per batch) leads to better calibration and higher MAUVE scores, due to reduced train-test distribution mismatch. Nucleus sampling probability $p$ during fine-tuning affects robustness: larger $p$ (more diverse samples) improves the quality estimator and self-correction.

Figure 4: Ablation study on fine-tuning hyperparameters $k$ and $n_y$ ; smaller $k$ yields better MAUVE scores.

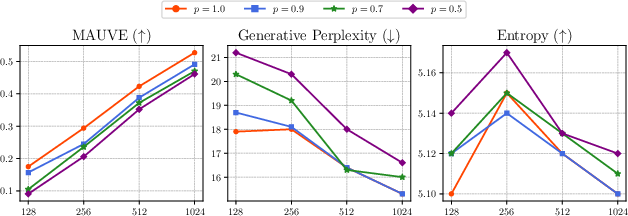
Figure 5: Ablation study on nucleus sampling $p$ ; larger $p$ during fine-tuning improves text quality and self-correction.

Implementation Considerations

Adapter Design: The auxiliary head can be implemented as a linear or attention-based projection on the final hidden state. LoRA adapters are recommended for large models.
Loss Function: Use binary cross-entropy for per-token quality, regularized by the original MDM loss.
Data Efficiency: Multiple unmasking sets per batch and stop-gradient on the MDM head improve efficiency.
Inference: Remasking and unmasking are performed in a single forward pass; loop-based refinement can be added for diversity.
Scaling: PRISM is effective across model sizes (30M–8B) and domains (Sudoku, text, code), with minimal compute requirements for fine-tuning.

Implications and Future Directions

PRISM provides a theoretically grounded, efficient, and scalable mechanism for self-correction in MDMs, overcoming limitations of prior approaches. The framework is applicable to any pretrained MDM without architectural changes, and enables robust per-token quality estimation for remasking. Empirical results demonstrate strong gains in sample quality and error correction, especially in low-step inference regimes.

However, the per-token quality score is based on posterior marginals and may not capture global reasoning errors. Future work should explore extensions to detect and correct global inconsistencies, potentially integrating verifier models or structured reasoning modules. The flexibility of MDMs and PRISM's plug-and-play design offer promising avenues for building generative models that emulate human-like correction and reordering in discrete sequence synthesis.

Conclusion

PRISM establishes a principled, efficient, and scalable approach for equipping Masked Diffusion Models with provable self-correction. By fine-tuning a lightweight adapter to learn per-token quality scores, PRISM enables robust remasking and revision at inference, validated across multiple domains and model scales. The framework is theoretically justified, computationally efficient, and broadly applicable, representing a significant advance in the practical deployment of discrete diffusion models for generative tasks.