Planner Aware Path Learning in Diffusion Language Models Training (2509.23405v1)

Abstract: Diffusion LLMs have emerged as a powerful alternative to autoregressive models, enabling fast inference through flexible and parallel generation paths. This flexibility is enabled by new sampling strategies, or planners, that iteratively choose where to denoise along the sequence rather than sampling uniformly at random. However, by modifying reverse paths, planners introduce a mismatch between the uniformly random denoising paths used during training and the planning-based paths used at inference. In this work, we systematically investigate this mismatch and theoretically show that the standard discrete diffusion training evidence lower bound (ELBO) does not accurately describe a denoiser under non-uniform planning. To bridge this gap, we derive a new Planned Evidence Lower Bound (P-ELBO) that directly incorporates planner-based reverse dynamics into the training objective. Building on this, we propose Planner Aware Path Learning (PAPL), a simple and effective modification of the standard masked discrete diffusion loss that aligns training and inference under planned denoisers. Empirically, PAPL delivers consistent improvements across domains, including a 40% relative gain in protein sequence modeling, up to a 4x improvement in MAUVE for text generation, and a 23% relative gain in HumanEval pass@10 for code generation.

• The paper introduces Planner-Aware ELBO to correct the mismatch between uniform random training and planner-based inference in diffusion language models.
• It presents the PAPL framework that integrates a planner-weighted loss, yielding measurable improvements in protein, text, and code generation tasks.
• Empirical results show that PAPL accelerates convergence, enhances robustness, and scales efficiently, closing the train-test gap in generative modeling.

Planner-Aware Path Learning in Diffusion LLM Training

Introduction

This paper addresses a fundamental mismatch in the training and inference procedures of Diffusion LLMs (DLMs) for discrete sequence generation. While DLMs enable flexible, parallel generation by iteratively denoising masked tokens, practical inference almost always employs a planner—a strategy that selects which tokens to denoise next based on model confidence or other heuristics. However, standard DLM training assumes uniform random denoising, leading to a divergence between the training objective and the actual inference process. The authors formalize this mismatch, prove that the standard evidence lower bound (ELBO) is invalid under planner-based inference, and introduce a new Planner-Aware ELBO (P-ELBO). They further propose Planner-Aware Path Learning (PAPL), a practical training scheme that aligns the training loss with planner-based inference, yielding consistent improvements across protein, text, and code generation tasks.

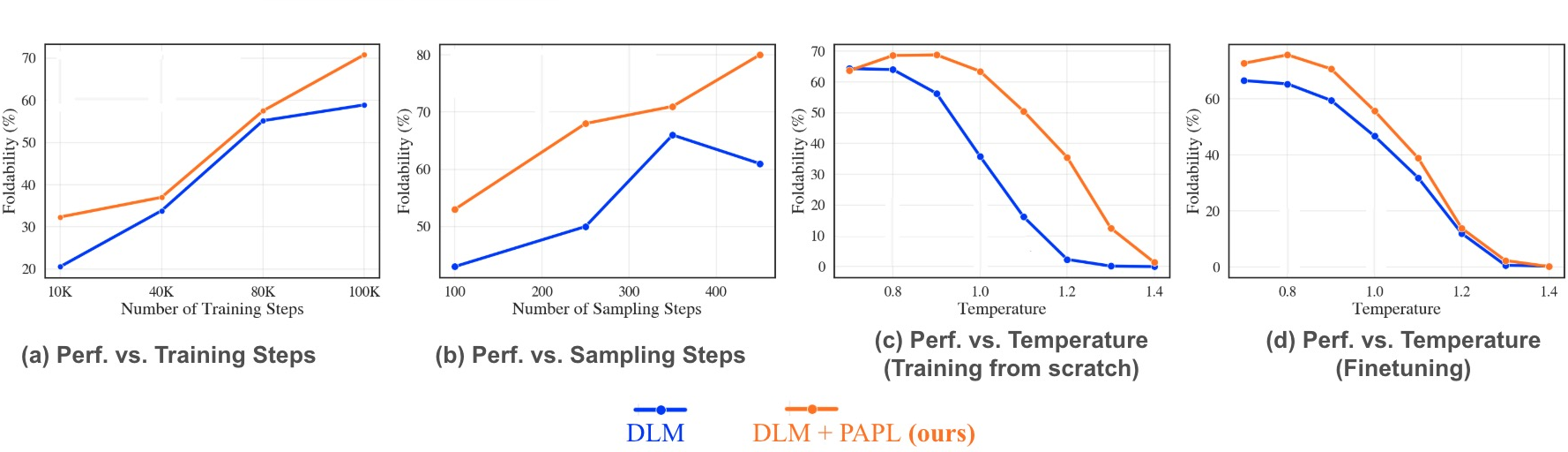
Figure 1: PAPL consistently improves over DLM across training, sampling steps, and temperature. (a) Faster convergence in training steps. (b) Higher performance across sampling steps. (c) More robust to temperature when training from scratch. (d) More robust to temperature when fine-tuning.

Theoretical Framework: Pathwise KL and Planner-Aware ELBO

The core theoretical contribution is the derivation of a planner-aware ELBO for DLMs. The authors model the denoising process as a discrete-time Markov chain, where each step consists of selecting a masked position (via a planner) and denoising it. They show that the standard DLM ELBO, which assumes uniform random selection, does not lower bound the log-likelihood of the data under planner-based inference. Specifically, for any non-uniform planner (e.g., greedy or softmax-based), the reverse process at inference time diverges from the process assumed during training, invalidating the standard ELBO.

To address this, the authors derive a pathwise KL divergence between the planner-based reverse process and an idealized reference process that always reconstructs the data. This leads to the Planner-Aware ELBO (P-ELBO), which consists of two terms:

• A planner-weighted cross-entropy over masked positions, reflecting the probability that the planner would select each position.
• A correction term that vanishes for uniform planners but is nonzero when the planner depends on the data or model predictions.

This framework unifies existing strategies (uniform, greedy, P2, etc.) as special cases and provides a principled loss for any planner-based sampling scheme.

Efficient Implementation: Planner-Aware Path Learning (PAPL)

While the P-ELBO is theoretically sound, its direct implementation is computationally prohibitive, especially for deterministic planners like greedy decoding, which require simulating the entire denoising path for each data point. To make planner-aware training practical, the authors propose several relaxations:

• Softmax Planner: Replace the hard argmax in greedy planners with a softmax over model confidences, parameterized by a temperature $\tau$. This yields a differentiable, planner-weighted distribution over masked positions.
• Stabilized Loss: Interpolate the planner-weighted loss with the standard uniform loss to reduce variance and improve training stability.
• One-Line Code Change: The final PAPL loss is a simple weighted cross-entropy, where the weight for each masked position is a convex combination of the uniform and planner-based probabilities.

The PAPL algorithm thus requires only a minor modification to standard DLM training, with negligible computational overhead.

Empirical Results

Protein Sequence Generation

PAPL demonstrates a 40% relative improvement in foldability over the DLM baseline on protein sequence generation, as measured by pLDDT, pTM, and pAE metrics. Notably, this improvement is achieved without sacrificing sequence diversity or entropy, and PAPL outperforms larger diffusion and autoregressive baselines.

Text Generation

On unconditional text generation (OpenWebText), PAPL achieves up to a 4× improvement in MAUVE and reduces generative perplexity by over 40% compared to prior diffusion models. These gains are consistent across different sampling budgets and hold under fast sampling regimes.

Code Generation

For code generation, PAPL yields a 23% relative improvement in HumanEval pass@10 (from 31.1 to 38.4) and improves pass@1 and infilling metrics as well. The improvements are robust across completion and infilling tasks, and the method scales to large codebases and long sequences.

Ablation and Stability

PAPL accelerates convergence, improves robustness to sampling temperature, and is stable across a range of planner hyperparameters. However, training with the pure PAPL loss (without interpolation) can lead to instability and poor convergence.

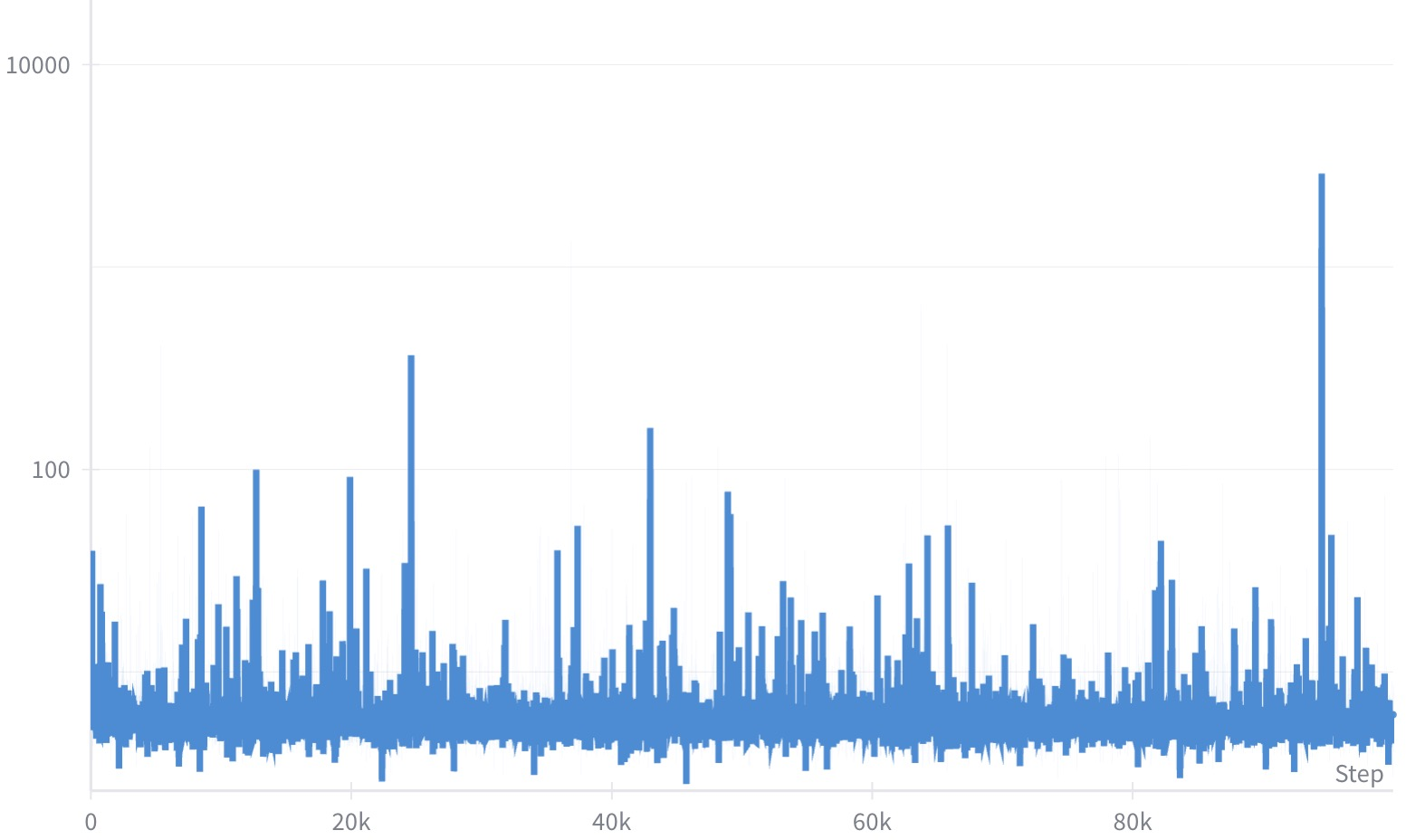
Figure 2: Training with pure PAPL loss ($\tau=1$) leads to unstable behavior, with large fluctuations in training (left) and poor convergence on validation (right).

Implementation Considerations

• Computational Overhead: PAPL incurs negligible additional cost compared to standard DLM training, as the planner weights can be computed in a single forward pass.
• Hyperparameters: The softmax temperature $\tau$ and planner weight $\alpha$ are critical; lower $\tau$ (sharper planners) and moderate $\alpha$ yield the best results.
• Generalization: The framework extends to planners with remasking (e.g., P2, RDM), though the computational cost increases with planner complexity.
• Deployment: PAPL-trained models are directly compatible with planner-based inference, closing the train-test gap and improving sample quality in real-world applications.

Implications and Future Directions

The introduction of P-ELBO and PAPL has several important implications:

• Alignment of Training and Inference: By matching the training objective to the actual inference procedure, PAPL eliminates a key source of suboptimality in DLMs and provides a principled foundation for planner-based generation.
• Unified View of Generation Order: The framework subsumes uniform, greedy, and more complex planners, enabling systematic exploration of generation order as a learnable or tunable component.
• Scalability: The simplicity and efficiency of PAPL make it suitable for large-scale models and datasets, including protein design, code synthesis, and text generation.
• Theoretical Rigor: The pathwise KL and planner-aware ELBO provide a rigorous basis for future work on order-aware generative modeling, including latent order learning and planner optimization.

Potential future developments include:

• Learning or meta-learning the planner itself, rather than fixing it a priori.
• Extending planner-aware training to continuous diffusion models and hybrid architectures.
• Exploring planner-aware objectives in other domains (e.g., vision, structured prediction) where generation order is ambiguous or task-dependent.

Conclusion

This work identifies and resolves a fundamental mismatch between training and inference in diffusion LLMs by introducing a planner-aware training objective and a practical implementation (PAPL). The approach yields substantial improvements in sample quality, convergence, and robustness across diverse domains, with minimal implementation complexity. The theoretical and empirical results establish planner-aware path learning as a critical component for advancing discrete generative modeling.