Decomposing the Entropy-Performance Exchange: The Missing Keys to Unlocking Effective Reinforcement Learning (2508.02260v1)

Abstract: Recently, reinforcement learning with verifiable rewards (RLVR) has been widely used for enhancing the reasoning abilities of LLMs. A core challenge in RLVR involves managing the exchange between entropy and performance of policies. Despite the importance of this exchange, a fine-grained understanding of when and how this exchange operates most effectively remains limited. To bridge this gap, we conduct a systematic empirical analysis of the entropy-performance exchange mechanism of RLVR across different levels of granularity. Specifically, we first divide the training process into two distinct stages based on entropy dynamics, i.e., rising stage and plateau stage, and then systematically investigate how this mechanism varies across stage-level, instance-level, and token-level granularitiess. Our analysis reveals that, in the rising stage, entropy reduction in negative samples facilitates the learning of effective reasoning patterns, which in turn drives rapid performance gains. Moreover, in the plateau stage, learning efficiency strongly correlates with high-entropy tokens present in low-perplexity samples and those located at the end of sequences. Motivated by these findings, we propose two methods that dynamically adjust the reward signal using perplexity and positional information to focus RL updates on tokens that exhibit high learning potential, achieving improvements compared to the baseline methods on various LLMs.

• The paper decomposes the RLVR training process, revealing that rapid entropy reduction in negative samples drives performance gains during the rising stage.
• It demonstrates that focused updates on high-entropy, low-perplexity tokens enhance formal and logical reasoning in large language models.
• The study proposes PPL-based and position-based reward shaping methods, significantly boosting model generalization on reasoning benchmarks.

Dissecting the Entropy-Performance Dynamic in Reinforcement Learning for LLMs

This paper presents an empirical analysis of the entropy-performance exchange within Reinforcement Learning with Verifiable Rewards (RLVR) for enhancing LLMs. The paper decomposes the RLVR training process into distinct stages and granularities to understand how entropy dynamics influence model performance, offering insights into more effective reward shaping techniques.

Stage-Level Analysis: Rising Versus Plateau

The paper identifies two primary stages in RLVR training: the rising stage, characterized by rapid performance gains and entropy reduction, and the plateau stage, marked by incremental improvements. During the rising stage, entropy reduction primarily occurs in negative samples, facilitating the establishment of effective reasoning patterns. The analysis of token distributions reveals a decrease in task-irrelevant tokens and an increase in reasoning-critical tokens, leading to a reduction in defective outputs such as format violations and irrelevant content.

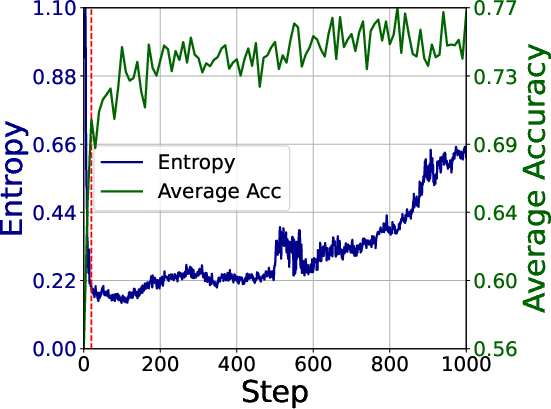
Figure 1: Entropy and accuracy trends on AIME24, AIME25 and MATH500 during GRPO training, with the red line indicating the transition from the rising stage to the plateau stage.

In the plateau stage, the focus shifts to a small subset of high-entropy, high-gradient tokens. Most token probabilities remain stable, with learning concentrated on tokens where probabilities in positive samples are reinforced and those in negative samples are suppressed. These impactful updates primarily target high-entropy tokens, which tend to produce larger gradients during backpropagation. The critical tokens are associated with formal reasoning, metacognitive reasoning, general semantic, and logical structuring.

Instance-Level Analysis: The Role of Perplexity

The paper analyzes the role of instance-level perplexity (PPL) to understand how sample quality affects optimization. The analysis indicates that learning signals are concentrated in low-PPL samples, representing more robust reasoning paths. Replacing tokens in low-PPL responses leads to smaller changes in the final solution's accuracy compared to high-PPL responses. Prioritizing low-PPL instances enhances RLVR effectiveness, while focusing on high-PPL samples leads to higher policy entropy and degrades response quality.

Token-Level Analysis: Positional Significance

The interplay between token position, entropy, and optimization impact reveals that token entropy follows a U-shaped distribution, with higher values at the start and end of sequences. Initial high-entropy tokens govern outcomes, while terminal high-entropy tokens reflect reasoning uncertainty. Optimizing tokens in later positions provides a more efficient learning signal.

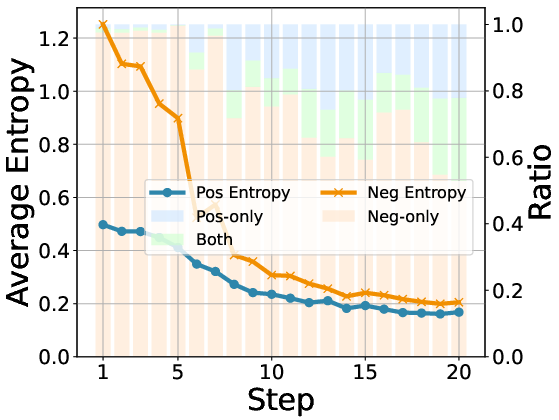
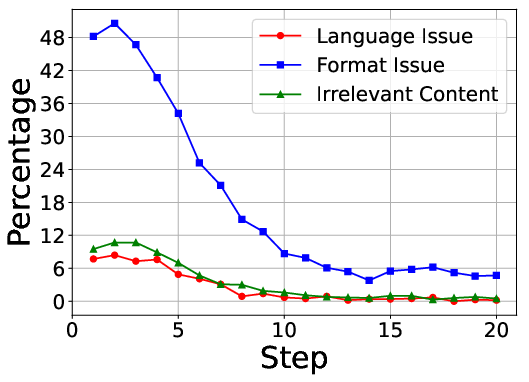
Figure 2: The sample distribution of the top 20\% tokens exhibiting the fastest entropy drop.

Advantage Shaping for Effective RLVR

Based on the empirical analysis, the paper proposes two reward shaping methods to dynamically re-weight token-level advantages. PPL-based advantage shaping adjusts token advantages to favor low-PPL samples, while position-based advantage shaping applies a position bonus to the token advantages, focusing optimization on the latter parts of reasoning sequences. The results demonstrate that the proposed methods achieve substantial improvements across various evaluation benchmarks, with enhanced generalization capabilities. The approaches sustain a higher level of entropy during the later stages of the plateau stage and result in longer responses with a notable increase in tokens related to formal reasoning and logic.

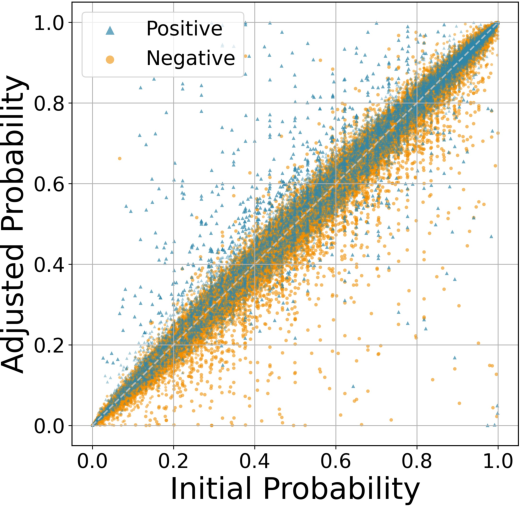
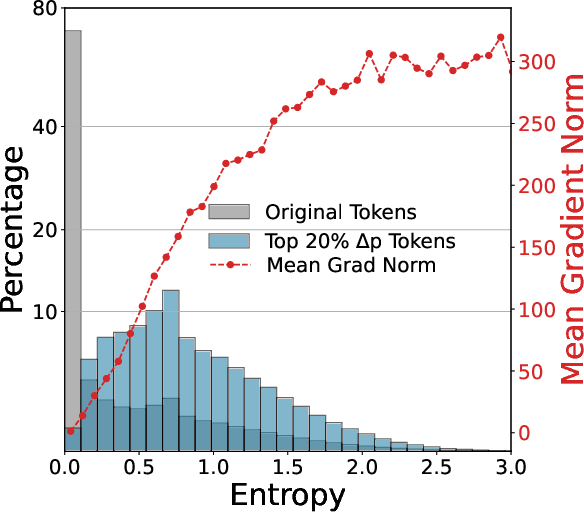
Figure 3: Probability shifts of tokens after gradient update.

Related Work

The paper references existing literature on RLVR for mathematical reasoning and the role of entropy of policy distribution in RLVR. The use of RL to improve mathematical reasoning in LLMs is well-established [DeepSeek-R1, openai2024b]. Furthermore, the significance of entropy in enhancing model capabilities during RLVR has been explored extensively [haarnoja2018soft, schulman2017proximal].

Conclusion

This paper provides a systematic investigation of the entropy-performance relationship in RLVR. The analysis reveals distinct dynamics across training stages, with initial performance gains emerging from entropy reduction in negative samples and later improvements depending on reinforcing high-entropy tokens in low-perplexity contexts. The proposed reward shaping techniques, leveraging perplexity and positional information, direct RL updates toward tokens with the highest learning potential and demonstrate performance improvements across multiple reasoning benchmarks. Future work will investigate their generalization to broader reasoning domains and integration with existing advanced RL methods.