Self-attention as an attractor network: transient memories without backpropagation (2409.16112v1)

Abstract: Transformers are one of the most successful architectures of modern neural networks. At their core there is the so-called attention mechanism, which recently interested the physics community as it can be written as the derivative of an energy function in certain cases: while it is possible to write the cross-attention layer as a modern Hopfield network, the same is not possible for the self-attention, which is used in the GPT architectures and other autoregressive models. In this work we show that it is possible to obtain the self-attention layer as the derivative of local energy terms, which resemble a pseudo-likelihood. We leverage the analogy with pseudo-likelihood to design a recurrent model that can be trained without backpropagation: the dynamics shows transient states that are strongly correlated with both train and test examples. Overall we present a novel framework to interpret self-attention as an attractor network, potentially paving the way for new theoretical approaches inspired from physics to understand transformers.

• The paper demonstrates that self-attention can be reformulated as an energy-based attractor network, enabling training without backpropagation.
• It introduces a recurrent update rule inspired by physical dynamics that creates transient memory states, validated on masked prediction and denoising tasks.
• The method uses pseudo-likelihood optimization to bridge transformer models with principles from Hopfield networks, offering an efficient alternative to traditional training.

Self-attention as an Attractor Network: Transient Memories Without Backpropagation

Introduction

The paper "Self-attention as an attractor network: transient memories without backpropagation" (2409.16112) presents a novel framework that reinterprets the self-attention mechanism in transformers as an attractor network. It extends the existing connection between neural networks and energy-based models, specifically Hopfield networks, by demonstrating that self-attention can be derived from local energy terms akin to pseudo-likelihood. This interpretation allows for training without backpropagation, leveraging recurrent neural dynamics to create transient states that correlate with both training and test data. The implications of this work extend to theoretical insights into transformer architectures, enriched by principles from physics like attractor dynamics.

Self-attention as an Attractor Network

Model Definition

The core of this study revolves around redefining self-attention in terms of energy dynamics typically found in physical systems. Here, a sequence of tokens, treated as vector spins, evolves with a specified dynamic equation reflecting local energy changes. Each token is embedded on a $d$-dimensional sphere, evolving according to:

$$\mathbf{x}_i^{(t+1)} = \sum_{j(\neq i)} \alpha_{i\gets j} \mathbb{J}_{ij} \, \mathbf{x}_j^{(t)} + \gamma \mathbf{x}_i^{(t)}$$

where $\alpha_{i\gets j}$ denotes an attention mask. The attention mechanism is derived by considering each token's dynamics as the derivative of a local energy function. This formulation diverges from traditional approaches by imposing an explicit token-dependence in attention weights, enhancing positional encoding effects in transformers.

Figure 1: Test examples appear as transient states of the dynamics, comparing models on masked prediction and denoising tasks.

Connection to Self-Attention

The self-attention mechanism is expressed akin to a derivative of the local energy associated with each token, achieved by tuning couplings between tokens and making simplifying assumptions about embeddings. The paper translates the self-attention update of $\mathbf{x}_i^\mathrm{OUT}$ into an energy-driven framework, unifying it with physical dynamics of vector spins, which is conducive for theoretical modeling and potentially advantageous in certain computational contexts.

Training Procedure

By bypassing backpropagation, the authors conceive a training regimen that minimizes a pseudo-likelihood-inspired loss across training samples. This method accentuates the energy minimization characteristic of pseudo-likelihood models, allowing for efficient optimization without reliance on deep gradient propagation. Such an approach not only enhances computational efficiency but also maintains task agnosticism, boasting consistent performance across different predictive tasks.

Results

The proposed model was evaluated on masked prediction and denoising tasks, using MNIST datasets for simplicity in benchmarking. Despite lacking trainable embeddings, self-attention exhibited notable efficacy in task completion, characterized by transient memory states indicative of attractor behavior.

In testing scenarios:

• Masked Prediction: Showed transient error minimization after one iteration.
• Denoising Task: Illustrated stable error reduction, achieving optimal predictions after multiple iterations.

Benchmarking against a full transformer block using backpropagation revealed that while the complete model achieved superior reconstruction capabilities, the simplified self-attention model retained valuable transient state characteristics relevant to memory dynamics in neural systems.

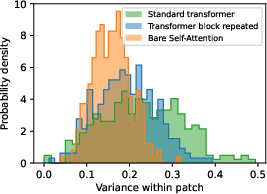
Figure 2: Bare Self-Attention predicts more uniform patches, demonstrating variance reduction with model simplification.

Discussion

This paper bridges the conceptual gap between self-attention mechanisms and attractor network theory. By reducing the complexity of the self-attention layer to align with physics-based attractor models, it offers an abstract yet practical perspective on how transformers might be understood and optimized beyond conventional deep learning paradigms. Although the innovative network falls short of full transformer capabilities in total reconstruction tasks, its simplicity supports potential theoretical and practical applications, especially when addressing dynamics analogous to physical systems of spins.

The implications extend toward novel training methodologies and theoretical exploration, hinting at expansive potential in scaling such architectures for broader application contexts. Prospective developments could involve the integration of more sophisticated embedding strategies or hybrid models combining backpropagation with energy-based learning, thereby enhancing adaptability in complex data environments.

Conclusion

The framework elucidated in this study is a promising step towards demystifying transformer architectures, casting them as energy-based systems derived from physical intuition. This work not only endorses innovations in understanding neural network functions through theoretical lenses but also sets a precedent for future explorations into energy-efficient and potentially more explainable AI systems. As such models integrate more closely with diverse neural paradigms, their applicability in cutting-edge AI tasks could significantly expand.

---

This essay synthesizes the core findings and methodologies of the referenced paper, aligning them with broader AI research trajectories. The open-source availability of code used in this research invites further experimentation and validation, potentially catalyzing subsequent innovations within the AI research community.