Greedy Coordinate Gradient Algorithm

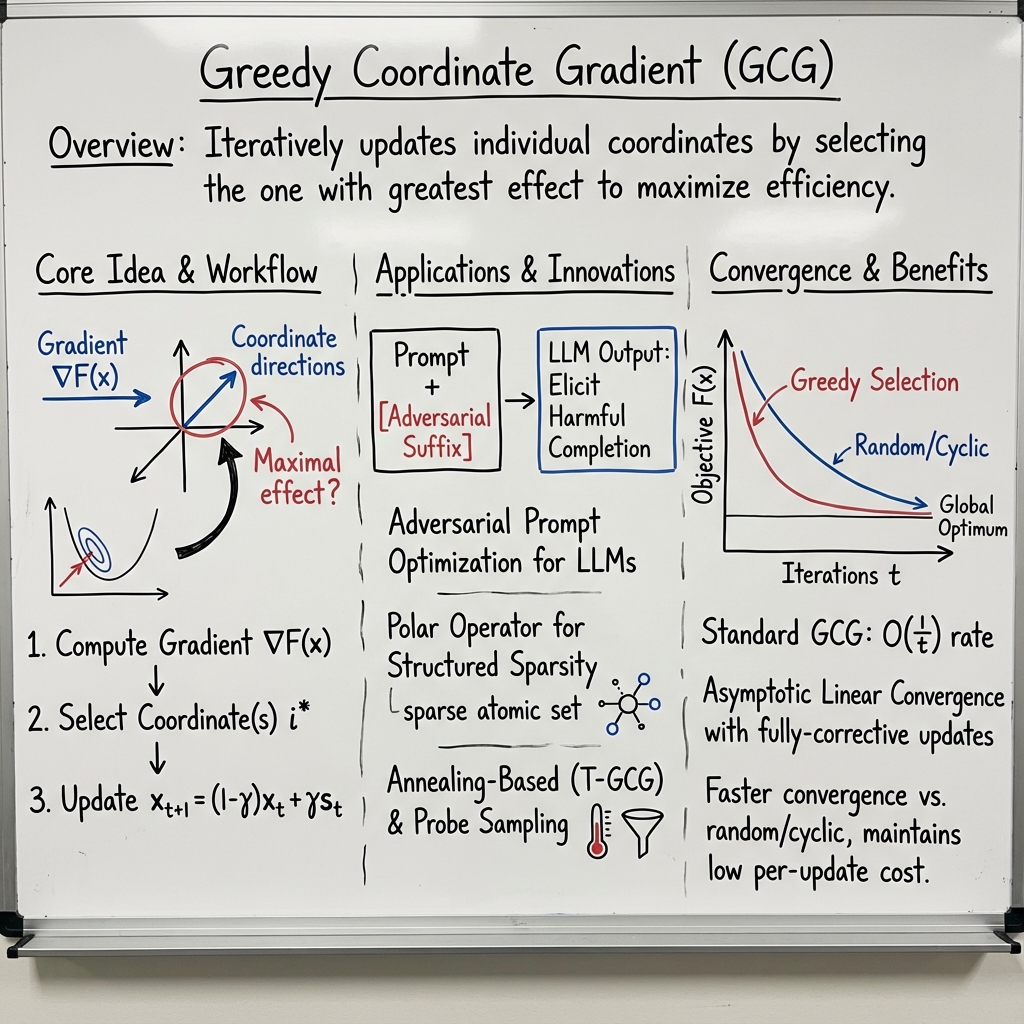
• GCG algorithm is an iterative method that selects the coordinate with the highest gradient impact, ensuring effective updates in high-dimensional, sparse environments.
• It employs polar operators and annealing-inspired sampling to solve structured sparsity and adversarial prompt optimization problems efficiently.
• GCG demonstrates O(1/t) convergence for convex objectives and shows superior performance compared to randomized methods in experimental evaluations.

The Greedy Coordinate Gradient (GCG) algorithm is a class of iterative optimization methods that update individual coordinates in high-dimensional problems by selecting the coordinate with the greatest effect, typically according to gradient magnitude or descent potential. First formalized as an extension of the classical conditional gradient (Frank–Wolfe) paradigm to structured sparse optimization (Yu et al., 2014), GCG-type approaches now encompass a spectrum of methods for convex, nonsmooth, and composite objectives. Modern instantiations—especially in adversarial prompting for LLMs—use stochastic, greedy, and annealing-augmented coordinate selection to maximize optimization efficiency and attack success rates.

1. Principle and Generic Workflow

At each iteration, GCG computes the gradient $\nabla F(\mathbf{x})$ of the objective $F$, then selects a coordinate $i^*$ (or a block of coordinates) to update. The canonical GCG update for a smooth convex function is: $$\mathbf{x}_{t+1} = (1 - \gamma_t) \mathbf{x}_t + \gamma_t \mathbf{s}_t$$ where $\mathbf{s}_t$ is obtained by solving

$$\mathbf{s}_t = \arg \min_{\mathbf{s} \in \mathcal{C}} \langle \mathbf{s}, \nabla f(\mathbf{x}_t) \rangle$$

with $\mathcal{C}$ being the atomic set (e.g., low-rank, group-sparse, or simplex atoms). The step size $\gamma_t$ is typically determined via line search or preset schedules.

In discrete adversarial contexts (e.g., prompt optimization for LLM jailbreaks), the suffix tokens to be optimized are indexed, and for each coordinate, the method computes token-wise gradients. The greedy step replaces the token yielding maximal marginal reduction in adversarial loss, often via a Top-$k$ strategy or stochastic softmax sampling (Tan et al., 30 Aug 2025).

2. Polar Operator and Structural Enhancement

A distinguishing feature of generalized GCG for structured sparsity is the use of a polar operator to efficiently solve the linear subproblem over nontrivial atomic sets (Yu et al., 2014): $$\mathbf{s}_t = \arg \min_{s \in \mathcal{C}} \langle s, \nabla f(\mathbf{x}_t) \rangle$$

Efficient evaluation of this operator is critical when the atomic structure is combinatorial or high-dimensional (e.g., dictionary learning, overlapping group lasso). The subproblem can often be reduced to a maximization over the support set, or solved via dual reformulation exploiting symmetry, low-rank, or separable structure—dramatically lowering per-iteration complexity.

Further acceleration is realized by interleaving global GCG steps with fixed-rank local subspace optimization. Specifically, after a finite number of GCG iterates, the algorithm restricts the search to the subspace spanned by previously selected atoms (or rank components), and performs a convex minimization over this subspace: $$\min_{\alpha \in \mathbb{R}^k} f(U\alpha V^\top) + \lambda \mathcal{R}(U\alpha V^\top)$$ where $U$, $V$ are basis matrices and $\alpha$ is a low-dimensional parameter block.

3. Convergence Properties

For convex structured sparsity objectives, standard GCG enjoys an $\mathcal{O}(1/t)$ convergence rate (Yu et al., 2014): $$F(\mathbf{x}_t) - F(\mathbf{x}^*) \leq \mathcal{O}(1/t)$$

Extensions to fully-corrective GCG in Banach spaces yield sublinear and, under certain regularity and quadratic growth, asymptotic linear convergence (Bredies et al., 2021). The iterative fully-corrective update solves for coefficients over active atoms, enabling aggressive pruning and rapid descent in function value: $$u_{k+1} = \arg\min_{u \in \operatorname{cone}(\mathcal{A}_k^+)} F(Ku) + \kappa_{\mathcal{A}_k^+}(u)$$

For block-separable and non-negative quadratic objectives, GCG-type coordinate descent achieves monotonic objective reduction and, under error bounds, linear convergence (Wu et al., 2020). Greedy selection accelerates convergence versus cyclic or randomized counterparts while maintaining similar per-update cost, provided full gradient bookkeeping is employed.

4. Extensions: Robust, Private, and Accelerated GCG

Robust supervised learning with coordinate descent employs GCG where each coordinate update leverages robust univariate partial derivative estimators (Median-of-Means, Trimmed Mean, Catoni–Holland) instead of full-gradient robustification, yielding statistical reliability under heavy-tailed or contaminated data with low computational overhead (Gaïffas et al., 2022). Theoretical generalization error bounds combine geometric decay (due to strong convexity) and effectively bounded statistical error per coordinate.

In the high-dimensional differential privacy setting, DP-GCD privately selects the coordinate of maximal scaled gradient magnitude using report-noisy-max and performs a noisy coordinate descent step (Mangold et al., 2022):

• Selection: $$j_t = \arg\max_{j' \in [p]} |\nabla_{j'} f(w^t) + \chi_{j'}^t| / \sqrt{M_{j'}}$$
• Update: $$w^{t+1} = w^t - \gamma_{j_t}(\nabla_{j_t} f(w^t) + \eta_{j_t}^t) e_{j_t}$$ with noise scales calibrated to ensure $(\epsilon, \delta)$-DP. Utility bounds are logarithmic in the ambient dimension for quasi-sparse solutions.

Accelerated greedy coordinate methods, such as AGCD and ASCD, integrate Nesterov-like acceleration frameworks. AGCD updates both $x$ and $z$-variables greedily (Lu et al., 2018): $$y^k = (1 - \theta_k) x^k + \theta_k z^k,\quad j_k = \arg\max_i \{| \nabla_i f(y^k)| / \sqrt{L_i} \}$$ with

$$x^{k+1} = y^k - [1 / L_{j_k}] \nabla_{j_k} f(y^k) e_{j_k}, \quad z^{k+1} = z^k - [1 / (n L_{j_k} \theta_k)] \nabla_{j_k} f(y^k) e_{j_k}$$

For accelerated $O(1/k^2)$ rates, a technical condition relating aggregate improvement across coordinates to greedy updates must hold.

5. Recent Innovations: Adversarial Prompt Optimization and Scaling Challenges

GCG has been widely adopted for optimization-based jailbreaking of LLMs, wherein it crafts adversarial suffixes augmenting a prompt to elicit harmful completions (Tan et al., 30 Aug 2025, Zhao et al., 2 Mar 2024, Zhang et al., 2 May 2024, Li et al., 11 Dec 2024, Jia et al., 31 May 2024). The central iterative step is: $$\mathbf{s}^\star = \arg\min_{\mathbf{s} \in \mathcal{V}^l} -\log p(y \mid x, \mathbf{s})$$ where $\mathcal{V}$ is the token vocabulary and $\mathbf{s}$ is the adversarial suffix.

Scaling up adversarial search for larger models introduces efficiency bottlenecks and landscape non-convexity (Tan et al., 30 Aug 2025). Simulated annealing-inspired temperature-based sampling (T-GCG) diversifies search by softmax sampling token candidates and probabilistic acceptance of loss-improved suffixes: $P(x_j) \propto \exp(-g_j^{(i)} / T_1)$

$P(s_b) \propto \exp(-\Delta \ell_b / T_2)$

with careful tuning of $T_1$, $T_2$, and scaling factors. This approach mitigates local minima, but semantic evaluation with GPT-4o highlights that prefix-based heuristics may overestimate attack effectiveness.

To accelerate GCG in resource-intensive settings, probe sampling leverages a lightweight draft model to filter candidates, dynamically adapting the number of candidates evaluated by the heavy target model according to a probe agreement score (Zhao et al., 2 Mar 2024). This adaptive filtering achieves up to $5.6 \times$ speedup, with equal or improved attack success rates.

Further enhancements include multi-coordinate updating (Jia et al., 31 May 2024, Li et al., 11 Dec 2024), momentum-augmented gradients (MAC), and gradient-based index selection (MAGIC), which exploit gradient sparsity and history to reduce redundant updates, accelerate convergence, and support transferability.

6. Theoretical Guarantees and Practical Impact

The theoretical foundation of GCG for convex composite and structured sparse objectives is well established, with $\mathcal{O}(1/t)$ sublinear convergence, global error bounds, and, under additional regularity, asymptotic linear rates (Yu et al., 2014, Bredies et al., 2021). For block-separable, $L_1$-regularized, and box-constrained problems, greedy coordinate descent achieves linear convergence rates independent of dimension in practice (Karimireddy et al., 2018).

Numerical experiments and empirical studies consistently show that greedy selection—in both conventional sparse estimation and adversarial LLM context—dramatically improves convergence speed, robustness, and attack success rate relative to uniform or random coordinate selection. GCG variants outperform cutting-plane methods, proximal gradient algorithms, and randomized coordinate descent in efficiency and solution quality, particularly as problem dimensionality increases or solution sparsity prevails.

7. Limitations, Extensions, and Open Directions

While GCG and its derivatives have demonstrated superior efficiency and robustness, scalability remains a challenge for larger models or loss landscapes with intricate non-convexity. Prefix-based evaluation metrics may overstate attack transferability compared to semantic assessment (Tan et al., 30 Aug 2025). Adaptive diversification strategies, annealing-inspired sampling, and multifaceted guidance (multi-coordinate, initialization, and diversified target templates) have improved effectiveness but require further systematic exploration, especially for transfer attacks and alignment defenses (Zhang et al., 2 May 2024, Jia et al., 31 May 2024, Li et al., 11 Dec 2024).

Recent advances suggest promising routes for combining GCG with structure-exploiting acceleration, stochastic relaxation, and robust selection mechanisms—spanning submodular maximization (Sakaue, 2020), high-dimensional privacy (Mangold et al., 2022), and optimization-based LLM jailbreak.

---

Summary Table: Core Innovations in GCG Algorithms

Variant / Enhancement	Key Mechanism	Impact
Polar Operator Optimization	Efficient subproblem over atomic set	Large-scale structured
Local Subspace Optimization	Fixed-rank refinement in spanned subspace	Accelerated convergence
Multi-Coordinate Update	Simultaneous updates in selected indices	Fewer iterations
Probe Sampling	Proxy model filtering and dynamic candidate evaluation	$\times$5.6 speedup
Momentum-Augmented (MAC)	Running average of gradients, smoothed updates	Stabilizes/accelerates
Annealing-Based (T-GCG)	Temperature-based sampling, probabilistic acceptance	Escapes local minima
Robust Univariate Estimators	Coordinate-wise robustification of gradients	Resilience to outliers
DP-GCD	Noisy max selection, coordinate-wise noisy update	Logarithmic DP utility

---

The Greedy Coordinate Gradient algorithm, in its classical, robust, and adversarial forms, represents a versatile, structure-aware optimization paradigm effective for large-scale structured sparsity and adversarial search, with ongoing innovations to address scalability, robustness, and convergence in increasingly demanding operational regimes.