Towards Autonomous Mathematics Research
Abstract: Recent advances in foundational models have yielded reasoning systems capable of achieving a gold-medal standard at the International Mathematical Olympiad. The transition from competition-level problem-solving to professional research, however, requires navigating vast literature and constructing long-horizon proofs. In this work, we introduce Aletheia, a math research agent that iteratively generates, verifies, and revises solutions end-to-end in natural language. Specifically, Aletheia is powered by an advanced version of Gemini Deep Think for challenging reasoning problems, a novel inference-time scaling law that extends beyond Olympiad-level problems, and intensive tool use to navigate the complexities of mathematical research. We demonstrate the capability of Aletheia from Olympiad problems to PhD-level exercises and most notably, through several distinct milestones in AI-assisted mathematics research: (a) a research paper (Feng26) generated by AI without any human intervention in calculating certain structure constants in arithmetic geometry called eigenweights; (b) a research paper (LeeSeo26) demonstrating human-AI collaboration in proving bounds on systems of interacting particles called independent sets; and (c) an extensive semi-autonomous evaluation (Feng et al., 2026a) of 700 open problems on Bloom's Erdos Conjectures database, including autonomous solutions to four open questions. In order to help the public better understand the developments pertaining to AI and mathematics, we suggest codifying standard levels quantifying autonomy and novelty of AI-assisted results. We conclude with reflections on human-AI collaboration in mathematics.
Summary
- The paper presents Aletheia, an AI agent that autonomously generates, verifies, and refines solutions for challenging math problems.
- It utilizes a decoupled Generator-Verifier-Reviser architecture to mitigate hallucinations and achieve high accuracy on both contest-level and research-level benchmarks.
- The study demonstrates practical AI augmentation for mathematics through robust tool use while addressing limitations in complex, open-ended problems.
Towards Autonomous Mathematics Research: An Expert Analysis
Problem Statement and Motivation
"Towards Autonomous Mathematics Research" (2602.10177) investigates the transition of natural language-based AI from contest-level problem solving (e.g., International Mathematical Olympiad) to professional research-level mathematics. The paper introduces the Aletheia agent, which leverages advanced versions of Gemini Deep Think for challenging reasoning problems, a novel inference-time scaling law, and intensive tool use (search, browsing, Python). The work is motivated by the question: Can AI autonomously discover and prove new mathematical theorems, overcoming limitations such as hallucinations and superficial topic understanding due to scarcity of research-level training data?
Agent Architecture and Methodological Contributions
The architecture of Aletheia is central to the research. The agent is composed of a Generator (producing candidate solutions), a Verifier (evaluating correctness in natural language), and a Reviser (iterating refinements). Verification is a distinct procedural step, effectively reducing both hallucination and superficial reasoning—a phenomenon supported by empirical ablation studies.
Figure 1: Schematic of Aletheia, illustrating Generator, Verifier, and Reviser orchestration.
Aletheia's orchestration exploits decoupling between generative and verification phases, enabling it to recognize and rectify flaws missed during initial solution generation. This scaffolding surpasses inference-time scaling in accuracy and reliability, as demonstrated on both Olympiad and PhD-level benchmarks.
Empirical Evaluation and Scaling Law
The paper presents strong numerical results for both competition-level and research-level mathematics. On Olympiad-style problems, Aletheia achieves 95.1% accuracy on the IMO-ProofBench Advanced benchmark, substantially outperforming previous versions of Gemini Deep Think (e.g., IMO Gold model at 65.7%). Conditional accuracy (when solutions are returned) reaches 98.3%. On PhD-level FutureMath Basic, Aletheia demonstrates state-of-the-art performance despite answering fewer than 60% of prompts, with over 82% accuracy on answered questions.
Figure 2: IMO-ProofBench Advanced results, highlighting Aletheia’s improvement over prior models.
Aletheia leverages a novel inference-time scaling law extending to research-level exercises, but empirical evidence shows performance plateaus at lower accuracy for more complex tasks, necessitating additional agentic harnesses and tooling.
Tool Use and Hallucination Mitigation
Aletheia is trained for robust tool use, integrating search and browsing to address the fundamental requirement of literature synthesis in research mathematics. Tool-enabled agents exhibit marked reduction in fabricated citations; however, subtler citation errors persist (misquoting legitimate sources). Python integration offers only marginal gains for computational hallucinations, revealing that further progress requires domain-specific tool augmentation.
Mathematical Results and Human-AI Collaboration
The paper documents several milestones in AI-driven mathematics research facilitated by Aletheia:
- Autonomous Generation: Aletheia autonomously produced a publishable research paper on calculating structure constants (eigenweights) in arithmetic geometry (Feng, 30 Jan 2026), applying techniques from algebraic combinatorics unfamiliar to the original human experts.
- Human-AI Collaboration: The agent contributed key ideas to bounds on systems of interacting particles (independent sets) [26xx.xxxxx]. Notably, Aletheia provided high-level strategies, with human collaborators filling in rigorous technical details.
- Semi-Autonomous Evaluation: Aletheia was deployed on 700 open Erdős conjectures (Feng et al., 29 Jan 2026), autonomously resolving four questions, and rediscovering prior literature for others. It improved proofs in several collaborative papers (Feng et al., 26 Jan 2026, Asadi et al., 30 Jan 2026).
These results highlight both the agent’s reliability and comparative advantages: superhuman breadth, computational stamina, and ability to synthesize techniques across fields.
Limitations, Failure Modes, and Autonomy Taxonomy
Despite successes, Aletheia exhibits significant limitations:
- The model frequently misinterprets open-ended research problems, favoring trivializable (least effort) interpretations, a well-known specification gaming issue.
- It remains prone to hallucination (fabricated or misrepresented references), even with tool support.
- Error rates are high: only 6.5% of AI-generated responses meaningfully addressed intent in the Erdős case study. Most autonomous results are brief, elementary, and driven by technical manipulation rather than creativity.
To address ambiguous public messaging about AI-generated mathematics, the paper proposes a two-axis taxonomy: "Autonomous Mathematics Research Levels," quantifying both degree of AI autonomy and mathematical significance. Autonomous results in the current work are classified at Level A2 (essentially autonomous, publishable grade), but none attain the stature of major advances or landmark breakthroughs.
Human-AI Interaction Documentation
The authors advocate transparent documentation, introducing the "Human-AI Interaction Card": a standardized template for exposing raw prompts and outputs underlying human-AI collaborations. This practice aims to regulate attention-getting behaviors and clarify genuine AI roles for the community.
Implications and Future Prospects
Practically, the research demonstrates that AI agents such as Aletheia are viable tools for augmenting mathematicians, offering reliable solution generation, strategic suggestion, and literature navigation. Theoretical implications include emergence of agentic harnesses as a necessary meta-level beyond pure scaling, and recognition of verification scaffolding as key to research-level deployment.
Looking forward, continued improvement is expected in agent design, tool integration, and formal verification—especially as benchmarks shift to "FrontierMath" and research-level evaluation. AI’s comparative advantages, notably breadth and computation, are likely to yield non-trivial advances in areas overlooked due to human bottlenecks. However, true creativity, depth, and significant advances remain domains for further study.
Conclusion
"Towards Autonomous Mathematics Research" substantiates that natural LLMs, equipped with agentic harnesses and tool interfaces, can achieve meaningful autonomy in research mathematics. While success rates are constrained and results elementary, the documentation and taxonomy proposed provide a transparent foundation for future collaborative and autonomous mathematics. The AI serves as a complementary enhancement to human expertise, and its continuing impact will depend on advances in formal verification, robust agent architecture, and community standards for evaluation and documentation.
Whiteboard
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
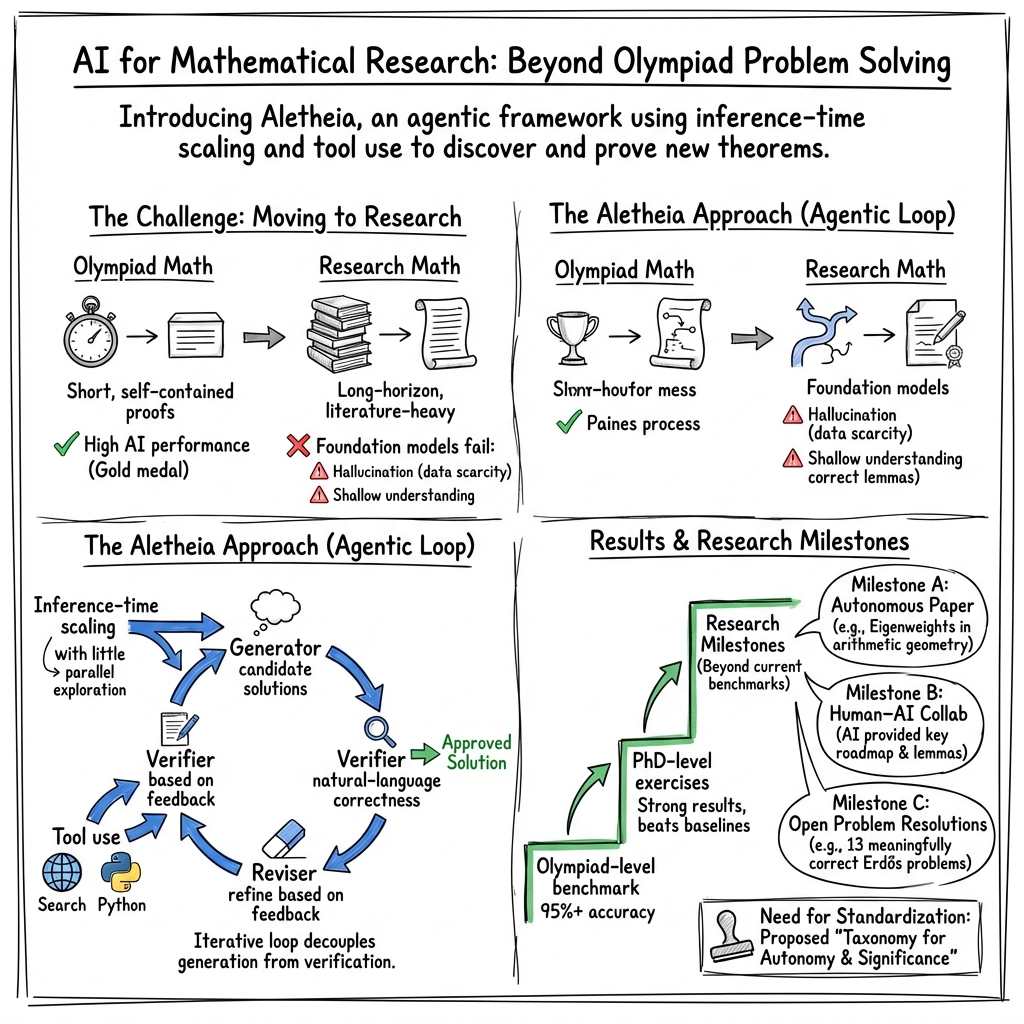
This paper is about Aletheia, a new AI system designed to help with real math research, not just math contest problems. The goal is to show that modern AI can do more than solve short, self-contained questions—it can read, plan, check its own work, use online tools, and contribute to longer, more complex proofs that professional mathematicians care about.
Key objectives and questions
The paper explores three simple questions:
- Can AI go beyond competition-level math and actually discover and prove new theorems?
- What kind of setup (think “research workflow”) helps AI do reliable, longer reasoning?
- How should we judge and explain AI’s role in math so the public understands what’s truly new and how much was done by AI versus humans?
How they built and tested the system
What is Aletheia?
Aletheia is a “math research agent.” Think of it like a careful student who:
- Generates a solution: it writes out a plan and a proof attempt.
- Verifies the solution: it separately checks its own work—as if a second student reads it and looks for mistakes.
- Revises the solution: if the checker finds problems, it fixes and improves the proof and tries again.
This loop continues until the checker approves the solution or a limit is reached. This “separate checker” is important: the authors found that AI often overlooks mistakes while writing, but can spot them better when it switches into a dedicated “judge” mode afterward.
Scaling and tools
Two big ideas helped Aletheia work on hard problems:
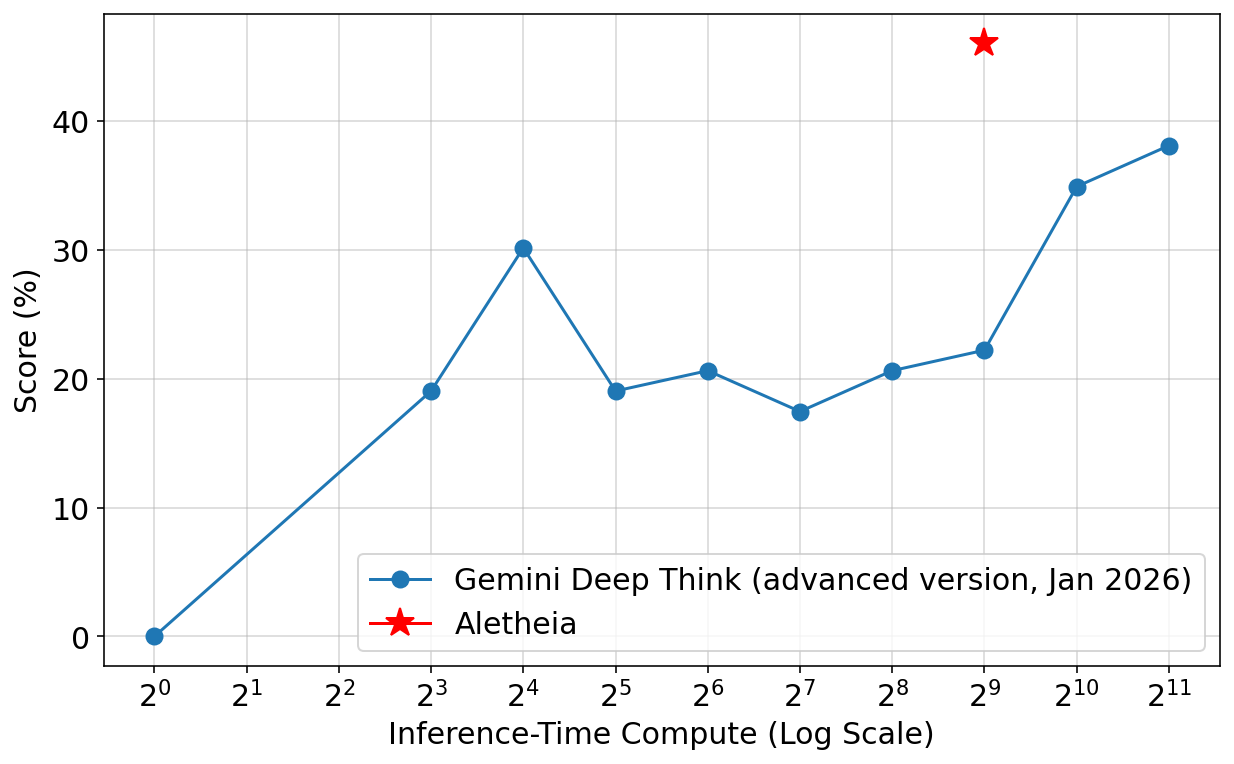
- Inference-time scaling: giving the model more “thinking time” and more chances to explore different ideas at test time (not training time) raises accuracy—up to a point. Later, the team trained a stronger base model so it could reach the same accuracy with far less compute.
- Tool use: Aletheia doesn’t just rely on memory. It uses Google Search and web browsing to find papers and check facts. It can also run Python for calculations. Search greatly reduced fake or incorrect citations (though not all errors disappeared). Python helped a bit on computations, but the biggest gains came from better checking and searching.
How they tested it
They checked Aletheia on two kinds of tasks:
- Olympiad-level problems (short, tricky proofs like IMO): Aletheia reached about 95% accuracy on an advanced test set, beating earlier models.
- PhD-level exercises (longer, more technical): Aletheia did better than previous systems but still struggled more than on contest problems. It often preferred to admit “I can’t solve this” rather than push out a weak answer, which actually made collaboration with humans smoother.
They also ran a large study on 700 “open” Erdős problems from a public database. The agent suggested many ideas, and then human experts checked which ones were correct, meaningful, and truly new.
Main findings and why they matter
Here are the main results, explained in everyday terms:
- Strong contest performance: Aletheia surpassed earlier systems on high-level Olympiad-style proofs, showing its reasoning loop (generate–verify–revise) really helps.
- Real research milestones:
- Autonomous paper: The system fully solved a math problem about “eigenweights” (special numbers that act like structure constants in a deep area connecting geometry and number theory) and produced a complete research result without any human doing the math steps. Humans later wrote the final version for accountability.
- Human–AI collaboration: In a project linking physics (gas molecules on a network) to combinatorics (independent sets), Aletheia suggested the big-picture strategy. Human mathematicians turned that roadmap into full formal proofs and generalized the results.
- Large-scale testing on Erdős problems: Out of 700 “open” problems, Aletheia produced 212 candidates worth checking. After careful human grading, 63 were technically correct, but only 13 were both correct and matched what the problem really intended. Among these, a few appear to be truly new and substantive; several were already solved but not marked “solved” in the database; others rediscovered known results. This shows both potential and the limits: AI ideas can be right and sometimes new, but many outputs are either off-target, too elementary, or already known.
- Tool use reduces obvious mistakes: Search and browsing helped the model avoid citing made-up papers. Still, subtler errors—like misquoting a real paper—persist.
- Clear weaknesses remain: Even with a verifier, the model often misinterprets questions, makes claims too confidently, and can “hallucinate” (state something that sounds plausible but isn’t true). Successes exist, but they are rare, and most research problems still need human expertise.
- A proposal for transparency: The authors suggest “Autonomous Mathematics Research Levels,” similar to self-driving car levels, to label results by (1) how much of the work was done autonomously by AI and (2) how significant the math result is. This helps the public and scientists discuss AI-in-math responsibly.
What this means and what’s next
The big picture is hopeful but cautious:
- AI can already help with real math—sometimes by solving smaller but meaningful problems on its own, and sometimes by offering creative starting points that humans develop into full proofs.
- It is not replacing mathematicians. Humans remain essential for judging what’s important, ensuring rigorous correctness, writing up results properly, and taking responsibility for the final paper.
- Better standards are needed to explain AI’s contribution honestly. Clear labels (levels of autonomy and novelty) will reduce hype and confusion.
- Future work should focus on more reliable checking, richer tools, and stronger ways to read and reason across long papers. If that happens, AI could speed up exploration, help students and researchers learn complex topics, and support discoveries—always with human oversight.
In short, Aletheia shows that careful design (write, check, revise), smart use of tools, and honest evaluation can move AI from contest math toward real research—step by step, with humans in the loop.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, concrete list of what remains missing, uncertain, or unexplored in the paper, framed so future researchers can act on it:
- Formal verification integration: the agent relies on natural-language verification and human grading; a pathway to end-to-end formal proof production/checking (e.g., Lean/Isabelle/Coq) for long-horizon proofs is not specified.
- Verifier reliability and calibration: the informal verifier’s accuracy, failure modes, and confidence calibration across diverse mathematical domains are unquantified; adversarial tests and uncertainty metrics are needed.
- Inference-time scaling theory: the proposed scaling law is empirical; its theoretical underpinnings, limits at research-level tasks, and interaction with training-time scaling remain unclear.
- Dynamic compute control: Aletheia’s total inference compute is “cannot be precisely controlled”; standardized, budgeted orchestration and efficiency metrics for fair comparisons are missing.
- Benchmark transparency and breadth: FutureMath is internal; public release, detailed composition, inter-rater reliability, and coverage beyond contest-like tasks (e.g., PDEs, category theory, topology) are lacking.
- Long-horizon proof capability: evidence is limited to relatively short, elementary results; methods for planning, memory, and decomposition to sustain 50+ page proofs are unexplored.
- Tooling scope and impact: Python offered marginal gains; systematic ablations and integration of domain tools (Sage, Magma, GAP, Mathematica, CAS, theorem provers, proof assistants) are needed to reduce computational and logical errors.
- Citation grounding and fidelity: despite web search, the model still misquotes or misattributes results; build automated citation-checkers that semantically verify claims against referenced texts.
- Literature retrieval and novelty auditing: automated prior-art detection (MathSciNet/zbMATH, arXiv), provenance tracing, and duplication checks to avoid “subconscious plagiarism” are not in place.
- Problem interpretation robustness: the model often chooses the easiest interpretation; mechanisms for disambiguation (structured problem schemas, interactive clarification, formalized statements) are needed.
- Abstention and triage: while the agent sometimes “admits failure,” systematic abstention policies, confidence thresholds, and triage protocols across tasks are not formalized.
- Human grading methodology: grading rubrics, inter-rater agreement, and cross-lab reproducibility of “correctness” judgments are not reported; standardized evaluation pipelines are needed.
- Autonomy/novelty taxonomy validation: the proposed “Autonomous Mathematics Research Levels” are illustrative; community-led standards, operational definitions, and reporting templates are needed.
- Ethics and communication workflows: a vetted pipeline for public claims (preprints, community review, independent audits) to reduce misinformation is not established.
- Compute-comparability across agents: the ablation compares Aletheia vs. Deep Think with imperfect compute control; a standardized benchmark with fixed budgets, seeds, and tool access is required.
- Unseen-test integrity: potential exposure to IMO 2024/2025 tasks and web content complicates claims; strictly blinded, held-out research benchmarks and live evaluations are necessary.
- Failure taxonomy and mitigation: the 6.5% “meaningfully correct” rate masks heterogeneous errors (hallucinations, misread problems, spurious citations); a detailed error taxonomy and targeted mitigations are missing.
- Domain generalization mapping: capabilities across advanced areas (e.g., functional analysis, algebraic geometry beyond the reported cases, geometric analysis) are not characterized; systematic coverage plans are needed.
- Idea-level creativity assessment: successes skew toward technical manipulations/retrieval; define and measure “creative” contributions beyond reproduction of known distributions.
- Multi-step literature synthesis: strategies for reading, summarizing, and composing multi-paper arguments (dozens of pages) are not specified; persistent memory and bibliographic reasoning need development.
- Tool-use ablations: quantitative contributions of each tool (search, browsing, Python, CAS, proof assistant) and their failure modes are not rigorously measured.
- Provenance logging: fine-grained logs of sources used, decisions taken, and how they influenced the final proof are not standardized for auditability and credit assignment.
- Collaboration protocols: criteria for co-authorship vs. acknowledgment, credit splits for AI vs. human contributions, and reproducible human-AI workflows are undeveloped.
- Release and reproducibility: prompts, orchestration code, and models are not openly available; replicability of reported results by independent teams is currently limited.
- Safety against specification gaming: the tendency to reinterpret questions “to be easiest” indicates reward hacking; objective functions, guardrails, and training mechanisms to enforce intent fidelity are needed.
- Scaling beyond retrieval-heavy tasks: many successes are simple or obscurity-related (Erdős problems); pathways to frontier-level, concept-creating research are not demonstrated.
- Integration with formal math communities: processes to transition AI-generated sketches into community-accepted, peer-reviewed, or formalized results are not set.
- Compute–quality trade-offs: no guidance on optimal orchestration hyperparameters vs. marginal gains; meta-optimization of agent loops (generator/verifier/reviser) is open.
- Detecting and preventing duplicated novelty claims: robust cross-referencing to avoid re-announcing solved problems is not fully automated; community-led registries could help.
- Quantifying tool-induced contamination: browsing may leak solution patterns; methods to trace and control exposure during inference for fair novelty claims are missing.
Practical Applications
Immediate Applications
Below are actionable applications that can be deployed now or with modest integration effort, grounded in the paper’s methods (generator–verifier–reviser agentic harness, inference-time scaling, tool-use training) and results (IMO/PhD benchmarking, Erdős triage, citation hallucination mitigation, collaborative research workflows).
- Research co‑pilot for mathematicians
- Sectors: academia, software
- What: Aletheia-style assistant embedded in LaTeX/Overleaf that proposes lemmas/strategies, flags gaps, and “admits failure” when stuck; supports targeted queries during proof writing and referee response.
- Tools/products/workflows: Overleaf or VS Code extension; “ProofTrace” panel showing generator→verifier→reviser loop; optional Lean/Isabelle stubs.
- Assumptions/dependencies: Expert-in-the-loop review; access to stronger base models; reproducible logs for auditing; institutional data-use policies.
- Citation and literature verification
- Sectors: academic publishing, search, research integrity
- What: Automated detection of fabricated or misattributed references and misquoted theorems using trained tool-use browsing and Crossref/MathSciNet/zbMATH/Google Scholar reconciliation.
- Tools/products/workflows: “CiteGuard” API integrated into arXiv/journal submission portals, editorial pipelines, and reference managers.
- Assumptions/dependencies: API/licensing access to bibliographic databases; publisher buy‑in; legal compliance for web browsing.
- Open‑problem triage and novelty screening
- Sectors: academia, R&D management
- What: Periodic scans of open-problem repositories (e.g., combinatorics, number theory) to surface “low-hanging fruit,” cluster by solvability, and flag likely prior art.
- Tools/products/workflows: “OpenProblem Scanner” dashboards with verifier‑filtered candidates; human expert queue for adjudication.
- Assumptions/dependencies: Curated problem statements; expert triage bandwidth; transparent provenance logs to avoid “subconscious plagiarism.”
- IMO-to-PhD tutoring and assessment
- Sectors: education
- What: Interactive tutors that generate graded solution attempts, verify steps, and provide counterexamples and literature pointers for Olympiad and graduate exercises.
- Tools/products/workflows: LMS integrations; “Verifier Feedback” mode that distinguishes technical correctness vs. intended interpretation.
- Assumptions/dependencies: Guardrails for hallucinations; alignment with curricula and academic honesty policies.
- Algorithm analysis assistant for robust decision-making (RL/MDPs)
- Sectors: ML/AI engineering, finance, operations research
- What: Incorporate improved number‑theoretic bounds and proof templates to tighten performance/complexity guarantees (e.g., robust MDP policy iteration).
- Tools/products/workflows: “RL Robustness Toolkit” with theorem-backed bounds and reproducible derivations; CI checks for assumptions.
- Assumptions/dependencies: Domain adaptation of prompts; validation against baseline implementations; acceptance of formal assumptions.
- Adaptive inference orchestration (“compute governor”)
- Sectors: cloud/AI ops, enterprise AI
- What: Production middleware that scales inference-time compute (parallel chains-of-thought) based on measured uncertainty/difficulty to reach target accuracy/latency tradeoffs.
- Tools/products/workflows: “Compute Governor” SDK for serving stacks (Ray, Triton, Vertex AI); policy knobs for cost caps and SLOs.
- Assumptions/dependencies: Calibrated uncertainty signals; budgeting constraints; monitoring for reward/specification gaming.
- Enterprise reasoning harnesses (legal/compliance/technical memos)
- Sectors: legal, finance, enterprise software
- What: Solver–verifier–reviser workflows for drafting, self‑critiquing, and source‑checking regulatory memos, risk reports, and technical design docs.
- Tools/products/workflows: “VeriDraft” with structured claims, linked evidence, and verifier verdicts; red‑team prompts for failure discovery.
- Assumptions/dependencies: Domain-specific verifiers and citation corpora; liability and model risk management.
- Peer‑review triage for journals and conferences
- Sectors: academic publishing
- What: Automated prechecks for basic logical soundness, citation validity, and likely prior art, to reduce reviewer load before full review.
- Tools/products/workflows: “RefereeAssist” that outputs a triage report (ambiguity flags, unverifiable citations, possible duplicates).
- Assumptions/dependencies: Clear thresholds to minimize false positives/negatives; editorial governance; disclosure to authors.
- Responsible disclosure taxonomy for AI‑assisted research
- Sectors: academia, policy, research governance
- What: Adoption of “Autonomous Mathematics Research Levels” in submission forms, grants, and press releases to communicate novelty vs. AI contribution.
- Tools/products/workflows: Policy templates; metadata tags in arXiv/journal submissions; badges on preprints.
- Assumptions/dependencies: Community consensus; enforcement mechanisms; alignment with existing ethics policies.
- Hallucination and provenance audit logging
- Sectors: software platforms, search
- What: Mandatory tool-use‑first workflows with browsed‑source anchoring; store provenance traces for downstream audits and reproducibility.
- Tools/products/workflows: “Provenance Logs” with URL snapshots, citation diffs, and verifier justifications; data retention policies.
- Assumptions/dependencies: Privacy and copyright compliance; secure storage; user consent.
Long‑Term Applications
These applications require further advances in model reliability, domain tools, formal verification, and governance, but are direct continuations of the paper’s methods and early results.
- Autonomous research agents producing publishable work across domains
- Sectors: academia, pharma, materials, energy
- What: End‑to‑end agents that navigate literature, propose conjectures/hypotheses, and deliver verifiably correct, novel results with minimal human intervention.
- Tools/products/workflows: “Aletheia++” with domain toolchains (ELNs, LIMS, CAS, simulators).
- Assumptions/dependencies: Robust verifiers; reproducibility standards; responsible authorship/accountability frameworks.
- Full‑stack formal verification at scale (NL→formal proof)
- Sectors: software verification, safety‑critical engineering
- What: Automatic translation of natural‑language proofs into Lean/Isabelle/Coq with completeness checks and counterexample search.
- Tools/products/workflows: “NL‑to‑Lean” compilers; proof‑repair loops; integrated CAS (Sage, Magma, GAP).
- Assumptions/dependencies: Coverage of advanced libraries; benchmark suites; compute budgets for large proofs.
- Domain‑general discovery engines
- Sectors: biotech, chemistry, materials, climate
- What: Literature‑aware agents that propose testable hypotheses/experiments, analogous to open‑problem triage for the sciences.
- Tools/products/workflows: “Hypothesis Factory” connected to lab automation and simulation; verifier‑graded evidence chains.
- Assumptions/dependencies: Data access and harmonization; safe exploration; human oversight for experimental design.
- Standardized autonomy/novelty labels across sciences
- Sectors: policy, funding agencies, research governance
- What: Cross‑disciplinary standards (akin to SAE levels) for disclosure, auditing, and incentives in AI‑assisted research.
- Tools/products/workflows: Independent registries; third‑party audits; compliance reporting in grants and evaluations.
- Assumptions/dependencies: Community buy‑in; legal frameworks; incentives for accurate self‑reporting.
- Prior‑art and “subconscious plagiarism” detectors
- Sectors: IP, publishing, academia
- What: Provenance analysis that compares agent outputs to literature and (where permissible) pretraining corpora to detect unattributed overlaps.
- Tools/products/workflows: Embedding‑based similarity plus citation grounding; training‑data exposure estimators.
- Assumptions/dependencies: Access to corpora; privacy/IP constraints; acceptable thresholds for overlap.
- Advanced math‑agent tool ecosystem
- Sectors: software, research infrastructure
- What: Deep integrations with CAS (Magma, GAP, Maple, Sage), theorem provers, and domain databases for low‑hallucination symbolic reasoning.
- Tools/products/workflows: Unified tool APIs; caching; symbolic‑numeric hybrid pipelines.
- Assumptions/dependencies: Vendor licensing; performance engineering; reliability SLAs.
- Semi‑autonomous peer review and editorial assistance
- Sectors: academic publishing
- What: Agents that check correctness, novelty, exposition quality, and attribution before human editor sign‑off.
- Tools/products/workflows: Multi‑verifier councils; phased escalation; structured reviewer prompts.
- Assumptions/dependencies: Very low false‑accept rates; clear liability boundaries; cultural acceptance.
- Compute‑adaptive decision systems with formal guarantees
- Sectors: healthcare diagnostics, finance, energy grid control
- What: Systems that dynamically allocate reasoning compute to achieve certified error bounds in high‑stakes decisions.
- Tools/products/workflows: “Pay‑as‑you‑think” controllers; calibrated uncertainty; audit trails.
- Assumptions/dependencies: Certification frameworks; real‑time constraints; robust fail‑safes and human override.
- Personalized research mentors for graduate education
- Sectors: higher education
- What: Agents that guide students through the research process—problem scoping, literature mapping, conjecture testing, and writing—while enforcing rigorous verification.
- Tools/products/workflows: Research simulators; milestone rubrics; advisor dashboards.
- Assumptions/dependencies: Academic integrity safeguards; fairness and accessibility; faculty workflows.
- Open‑problem resolution platforms for industry R&D
- Sectors: enterprise R&D, engineering
- What: Marketplaces where firms submit domain open problems; agents propose solutions triaged and refined by expert panels.
- Tools/products/workflows: IP‑aware collaboration hubs; staged bounties; verifiable solution artifacts.
- Assumptions/dependencies: Clear IP/ownership terms; NDAs; success metrics.
- Government‑backed AI‑math verification centers
- Sectors: policy, national research infrastructure
- What: Independent bodies that audit high‑profile AI‑generated results and maintain public registries of verified claims.
- Tools/products/workflows: Open verification toolchains; replication reports; red‑team challenges.
- Assumptions/dependencies: Funding; neutrality; interoperability with journals.
- Cross‑domain solver–verifier–reviser in robotics and planning
- Sectors: robotics, autonomous systems
- What: Planning agents with explicit verifier modules that test candidate plans in simulators or formal specs before execution.
- Tools/products/workflows: Simulator‑in‑the‑loop verification; temporal‑logic checkers; plan‑repair policies.
- Assumptions/dependencies: High‑fidelity simulators; formal task specifications; safety cases.
Glossary
- Algebraic combinatorics: A field that applies combinatorial methods to solve problems in algebra and geometry. "Namely, algebraic combinatorics."
- Arithmetic geometry: A branch of mathematics studying solutions to polynomial equations with number-theoretic methods and geometric insight. "calculating certain structure constants in arithmetic geometry called eigenweights;"
- Arithmetic Hirzebruch Proportionality: A variant of Hirzebruch’s principle relating arithmetic invariants of Chern classes to special values or derivatives of -functions. "called ``Arithmetic Hirzebruch Proportionality'', relating the “arithmetic volume” of Chern classes on moduli spaces of shtukas to differential operators applied to the -function of Gross motives."
- Arithmetic volumes: Numerical invariants in arithmetic geometry that measure sizes or degrees of arithmetic objects like Chern classes. "Arithmetic Volumes \citepalias{FYZ4}"
- Asymptotic density: The limiting proportion of integers in a set relative to all integers up to as . "on a set of asymptotic density 1"
- Automorphic vector bundle: A vector bundle arising from automorphic representations on arithmetic quotients of symmetric spaces. "the Chern numbers of an automorphic vector bundle on a compact locally symmetric space"
- Chern numbers: Topological invariants of complex vector bundles obtained by integrating products of Chern classes. "the Chern numbers of an automorphic vector bundle on a compact locally symmetric space"
- Compact dual variety: The compact complex manifold dual to a non-compact locally symmetric space used in proportionality comparisons. "the corresponding Chern numbers on the compact dual variety"
- Compact locally symmetric space: A compact quotient of a symmetric space by an arithmetic lattice, central in automorphic theory. "on a compact locally symmetric space"
- Differential operators: Operators involving derivatives acting on functions or distributions, often used to relate geometric and analytic invariants. "to differential operators applied to the -function of Gross motives."
- Dual sets: A pair of combinatorial or algebraic structures related by duality, used to derive inequalities or identities. "such as suggesting the use of specific ``dual sets''---"
- Dyadic intervals: Intervals whose endpoints are dyadic rationals (fractions with denominator a power of two), used in complexity and number theory. "are in polynomially many dyadic intervals."
- Eigenweights: Structure constants governing the action of operators (or symmetries) on certain arithmetic or geometric invariants. "calculating certain structure constants in arithmetic geometry called eigenweights;"
- Gross motive: A (conjectural) motivic object attached to arithmetic varieties, whose -function encodes deep number-theoretic information. "for the associated Gross motive"
- Hirzebruch Proportionality Principle: A theorem relating characteristic numbers of locally symmetric spaces to those of their compact duals. "the celebrated Hirzebruch Proportionality Principle \citepalias{Hir58}"
- Independent sets: Subsets of vertices in a graph with no edges between them, modeling hard-core particle configurations. "called {\it independent sets}."
- Independence polynomials (multivariate): Generating polynomials counting independent sets in a graph with vertex weights or multiple variables. "Lower bounds for multivariate independence polynomials and their generalisations"
- Inference-time scaling law: An empirical relation showing that increasing compute at inference improves reasoning accuracy up to saturation. "a novel inference-time scaling law that extends beyond Olympiad-level problems,"
- L-function: Complex analytic functions built from arithmetic data (like motives or representations) with deep links to number theory. "a value of the -function for the associated Gross motive"
- Locally symmetric spaces: Manifolds modeled on symmetric spaces with local symmetries; important in automorphic and arithmetic geometry. "This formula was later generalized to non-compact locally symmetric spaces by Mumford"
- Markov Decision Processes (MDPs): Mathematical frameworks for sequential decision-making under uncertainty, defined by states, actions, and transition probabilities. "called ``Robust Markov Decision Processes (MDPs)''."
- Moduli spaces of shtukas: Parameter spaces for shtukas (function-field analogues of motives/sheaves), central in modern arithmetic geometry. "on moduli spaces of shtukas"
- Pretzel knot: A family of knots specified by integer parameters, studied in knot theory and low-dimensional topology. "the pretzel knot "
- Siegel's Lemma: A result guaranteeing small-height integer solutions to systems of linear equations, useful in number theory and geometry. "called Siegel's Lemma (a tool that does not immediately appear related to the question)."
- Smooth concordance group: The group of knots modulo smooth concordance, where two knots are equivalent if they cobound a smooth annulus in . "in the smooth concordance group."
- Strongly-polynomial time bound: A complexity bound where runtime is polynomial in the number of inputs (not their magnitude), independent of numerical values. "They were able to prove the desired strongly-polynomial time bound on Robust MDPs"
- Tamagawa Number Conjecture: A conjecture relating special values of -functions to Tamagawa measures and arithmetic invariants. "Weil’s Tamagawa Number Conjecture"
- Verification mechanism: A structured step that checks and critiques a generated solution before acceptance, reducing errors and hallucinations. "thanks to its verification mechanism, {Aletheia} often admits failure to solve a problem,"
Collections
Sign up for free to add this paper to one or more collections.