Long-horizon Reasoning Agent for Olympiad-Level Mathematical Problem Solving
Abstract: Large Reasoning Models (LRMs) have expanded the mathematical reasoning frontier through Chain-of-Thought (CoT) techniques and Reinforcement Learning with Verifiable Rewards (RLVR), capable of solving AIME-level problems. However, the performance of LRMs is heavily dependent on the extended reasoning context length. For solving ultra-hard problems like those in the International Mathematical Olympiad (IMO), the required reasoning complexity surpasses the space that an LRM can explore in a single round. Previous works attempt to extend the reasoning context of LRMs but remain prompt-based and built upon proprietary models, lacking systematic structures and training pipelines. Therefore, this paper introduces Intern-S1-MO, a long-horizon math agent that conducts multi-round hierarchical reasoning, composed of an LRM-based multi-agent system including reasoning, summary, and verification. By maintaining a compact memory in the form of lemmas, Intern-S1-MO can more freely explore the lemma-rich reasoning spaces in multiple reasoning stages, thereby breaking through the context constraints for IMO-level math problems. Furthermore, we propose OREAL-H, an RL framework for training the LRM using the online explored trajectories to simultaneously bootstrap the reasoning ability of LRM and elevate the overall performance of Intern-S1-MO. Experiments show that Intern-S1-MO can obtain 26 out of 35 points on the non-geometry problems of IMO2025, matching the performance of silver medalists. It also surpasses the current advanced LRMs on inference benchmarks such as HMMT2025, AIME2025, and CNMO2025. In addition, our agent officially participates in CMO2025 and achieves a score of 102/126 under the judgment of human experts, reaching the gold medal level.
First 10 authors:
Summary
- The paper introduces a novel hierarchical multi-agent system that integrates agentic reasoning, lemma summarization, and logical verification to enable deep Olympiad-level problem solving.
- It leverages Bayesian reinforcement learning for process verification, optimizing multi-round deduction and stabilizing high-confidence reasoning through hierarchical policy improvements.
- The method achieves state-of-the-art performance on competitive benchmarks by managing up to 512K context tokens and mitigating error propagation through systematic lemma memory.
Intern-S1-MO: Hierarchical Long-horizon Reasoning for Olympiad-Level Mathematics
Motivation: Context Scalability in Mathematical Reasoning
Large Reasoning Models (LRMs) have advanced the solution frontier for mathematical problems using CoT and RLVR protocols. Despite progress on problems like AIME, context length scaling remains a bottleneck for ultra-hard tasks such as those encountered at the International Mathematical Olympiad (IMO). Existing SOTA LRMs achieve up to 128K context tokens, yet human expert thinking and model token consumption grow exponentially with problem difficulty, rapidly outpacing available model capacity. Figure 1 illustrates the exponential growth of required tokens and demonstrates that Intern-S1-MO enables the use of up to 512K tokens per problem, supporting much deeper reasoning and achieving SOTA on challenging benchmarks.
Figure 1: As problem difficulty increases, both average human thinking time and model token consumption grow exponentially; Intern-S1-MO uses up to 512K tokens per problem and obtains SOTA results on mathematical benchmarks.
Hierarchical Multi-Agent Reasoning Framework
Intern-S1-MO is constructed as an LRM-based multi-agent system with three key agents: reasoner, summarizer, and verifier. The workflow is inherently multi-round and hierarchical. At each reasoning round, the reasoner produces candidate solution traces; the summarizer extracts and condenses exploratory reasoning into formal lemmas, which are passed to the verifier for logical validation. Validated lemmas are stored in a persistent lemma library, which is reincorporated in subsequent rounds as context, enabling lemma-rich exploration unconstrained by prompt size. A final modification loop refines the solution in response to verifier feedback until either successful validation or a rollout limit is reached.
Figure 2: Intern-S1-MO’s agentic framework employs recursive rounds of reasoning, lemma summarization, and verification to accumulate rigorously validated sub-results in persistent memory.
Lemma memory management markedly differs from prior tree-of-thought and parallel search approaches: Intern-S1-MO systematically condenses knowledge into validated sub-results that enable deeper deduction across rounds. This architecture directly addresses reasoning under strict context constraints and mitigates error propagation by explicit theorem verification.
RL Optimization: OREAL-H for Hierarchical Agentic Learning
To drive agentic improvement and learning, OREAL-H extends the Outcome Reward RL paradigm to hierarchical MDPs with multi-agent structure. The process verifier (PV) assigns natural language feedback and a continuous reward signal through multi-shot confidence aggregation. RL optimization proceeds via behavioral cloning for cold-start initialization, then switches to RL with conjugate Bayesian reward modeling for process verification outputs. The sparse/intermediate reward structure is implemented with temporal difference estimation and a lemma dependency graph, which propagates proof success downstream to intermediate lemmas and quantifies their contribution to solution synthesis.
Figure 3: A lemma dependency graph aggregates and quantifies lemma contributions across multiple rollouts, driving value estimation and structured RL advantage computation.
OREAL-H leverages Bayesian modeling for process verifier feedback, smoothing noisy step-level evaluations and denoising stochastic artifacts. The reward formulation computes the dominance probability over a “completely invalid” baseline, strongly suppressing false positives while maintaining gradient signal for high-confidence progress. This method supports stable and scalable agent training under imperfect process-level supervision.
Empirical Results and Performance
Intern-S1-MO sets new state-of-the-art marks across several competitive mathematics benchmarks:
- HMMT2025: 95% pass@1
- AIME2025: 96.6% pass@1
- CNMO2025: 232.4/260 points
- IMO2025 non-geometry: 26/35 points, matching silver medalist level
- CMO2025 (real test participation, human grading): 102/126 points, exceeding gold medal threshold
Performance gains are consistent across both calculation-centric and proof-oriented benchmark tasks. On IMO-level problems, Intern-S1-MO accounts for persistent partial progress, successfully constructs novel auxiliary lemmas, and surpasses inference methods restricted by one-pass context. The ablation study confirms every system component (multi-round reasoning, lemma verification, process validation, RL) yields non-redundant improvements, and the architecture is parameter-efficient.
Theoretical and Practical Implications
Intern-S1-MO demonstrates that systematic hierarchical reasoning, lemma-based memory, and process-aware RL collectively unlock deep solution capabilities for tasks beyond traditional LRM context bounds. The persistent lemma library and multi-agent architecture are theoretically significant: they enable SRLMs to simulate scratchpad-like state, facilitate iterative decomposition, and approach human-like problem decomposition patterns. Practically, these mechanisms allow LRMs to address a class of problems previously inaccessible to single-round or prompt-engineered methods, with robust verification mitigating error propagation.
The RL aspects, particularly Bayesian reward modeling and hierarchical TD advantage formulation, offer a template for future agentic optimization in language reasoning agents and mark a substantial advance beyond binary outcome-based RLVR training.
Future Directions
This work points towards scalable, agentic LRM systems capable of long-horizon deductive synthesis at or beyond human expert standards. Key open areas include further scaling of persistent memory architectures, automated lemma extraction verification, transferability to other domains (e.g., formal theorem proving, research mathematics), and integration with multimodal or tool-augmented frameworks.
Improving idiosyncratic insight detection (spark-of-insight problems, creative construction) remains a frontier, potentially addressable by policy architecture enhancements and meta-learning protocols. The paradigm demonstrated by Intern-S1-MO is likely to inform next-generation AI capable of rigorous cognitive tasks across both mathematical and broader scientific domains.
Conclusion
Intern-S1-MO advances the practical and theoretical frontier of long-horizon mathematical reasoning by integrating hierarchical multi-round agentic protocols, lemma memory management, robust verification, and process-aware RL training. These mechanisms collectively enable solutions to ultra-hard competition problems beyond the reach of existing context-constrained LRMs, demonstrated by gold/silver medal-level performance on real Olympiad datasets. The methodological innovations described herein will shape future research on scalable reasoning agents for complex intellectual domains.
Whiteboard
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper is about teaching an AI to solve very hard math problems, like those in the International Mathematical Olympiad (IMO). The authors built a special math “agent” called Intern-S1-MO that thinks in multiple rounds, writes down useful mini-results (called lemmas), and checks its own work. This helps the AI work through long, complex problems even when it can’t keep everything in its “short-term memory” at once.
What questions does the paper try to answer?
The paper focuses on three big questions:
- How can an AI solve ultra-hard math problems that need long, careful reasoning?
- Can the AI break a big problem into smaller, reusable pieces (lemmas) and remember them across multiple rounds?
- Can we train the AI to improve over time using feedback—not just for the final answer, but for the quality of its proof steps?
How does the AI work? (Methods explained simply)
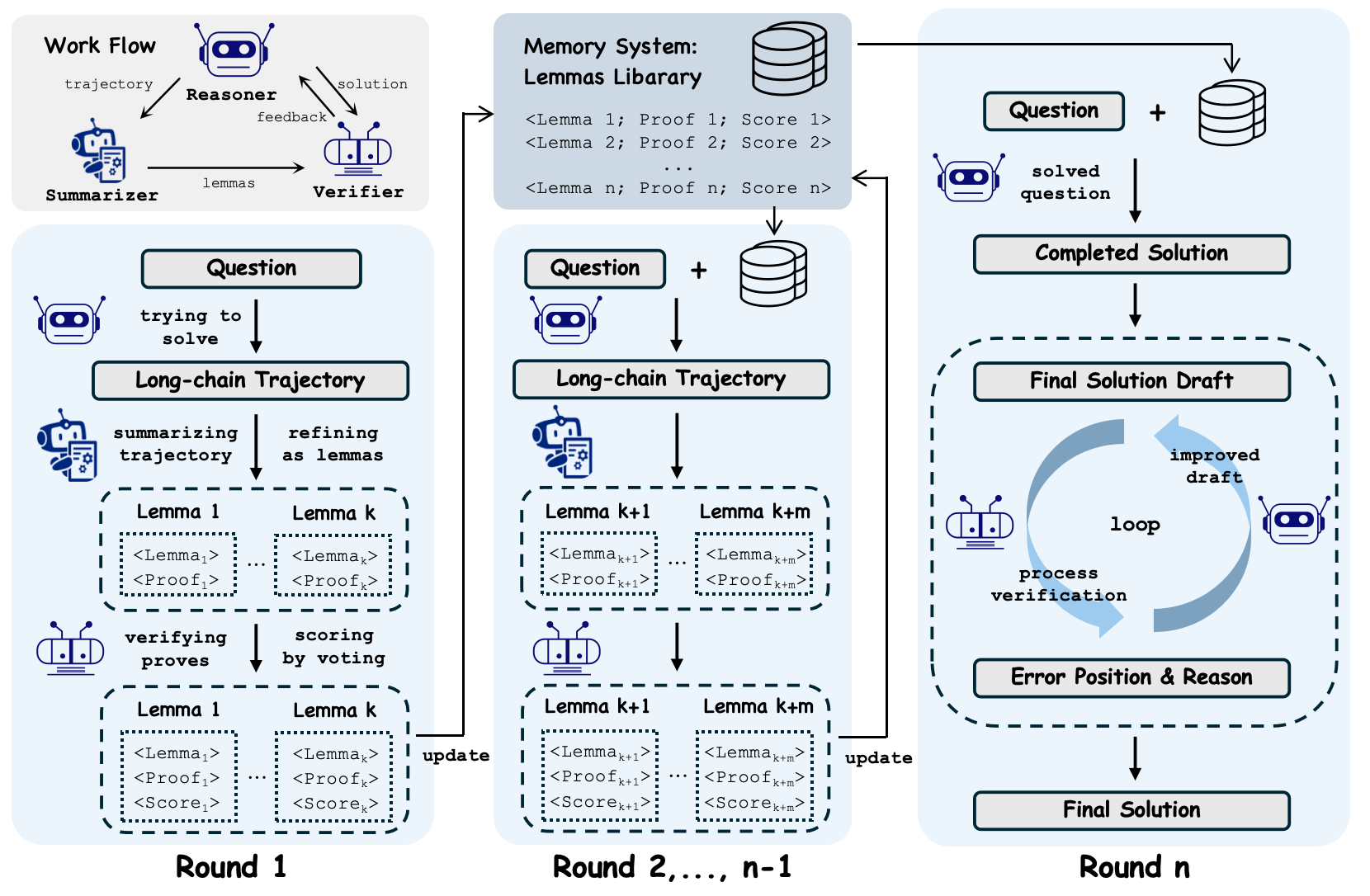
Think of solving an IMO problem like climbing a mountain: you need a plan, you might try different paths, and you keep notes so you don’t repeat mistakes. Intern-S1-MO works like a small team with different roles:
The “team” inside the AI
- Reasoner: Tries to solve the problem and discover helpful ideas.
- Summarizer: Writes down short, clear mini-results (lemmas) from the Reasoner’s work. A lemma is a small, true statement that helps prove a larger result—like a stepping stone.
- Verifier: Checks whether those lemmas and the final solution make sense and are logically sound.
How it solves problems step by step
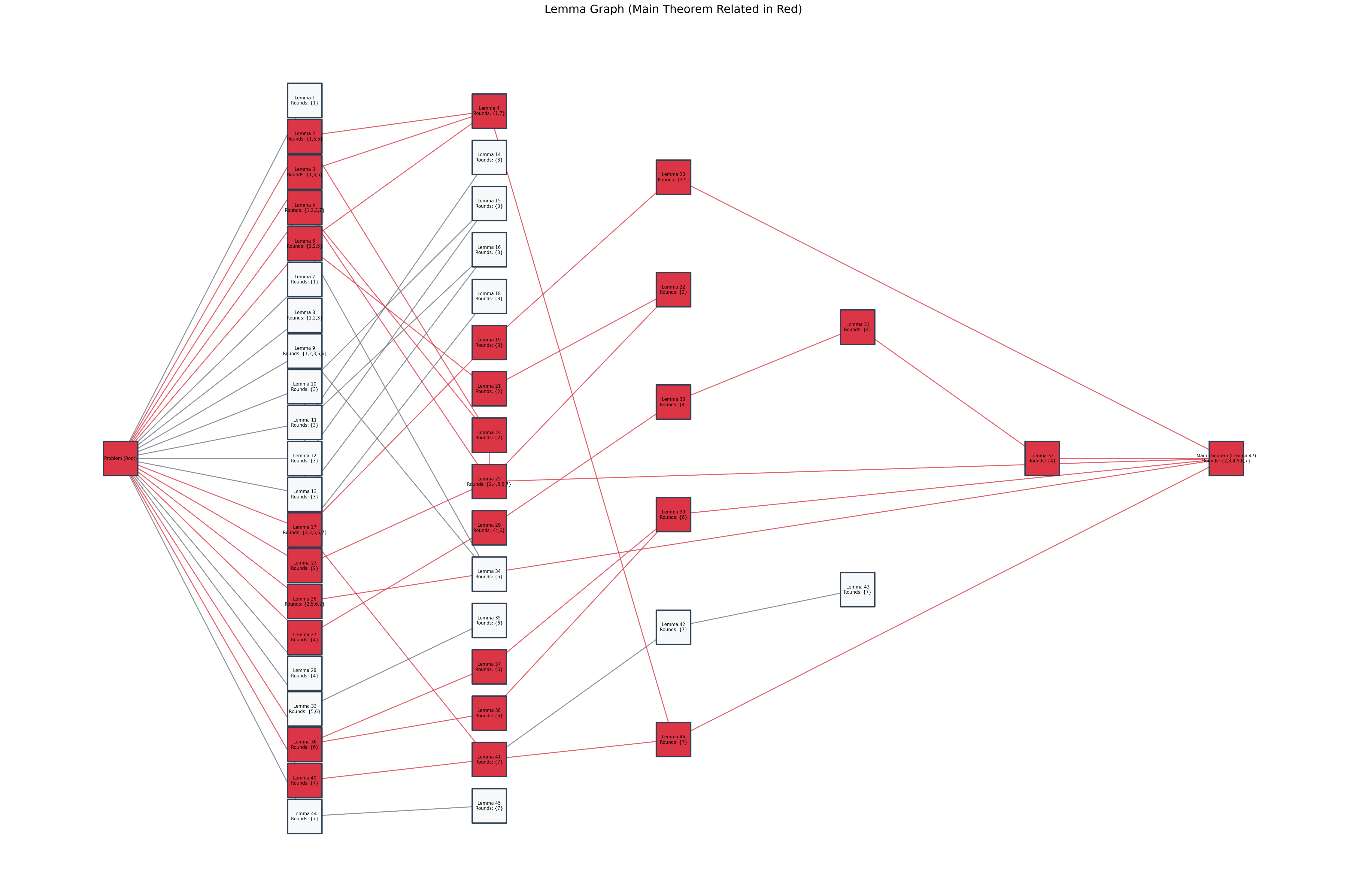
- Multi-round thinking: Instead of doing everything in one go (which can run out of memory), the AI thinks in several rounds. After each round, it saves important lemmas into a “lemma library”—like a notebook of proven facts it can reuse later.
- Lemma library: This is a compact memory that stores short, verified statements. It keeps the important parts and avoids repeating wasted exploration.
- Verification: The AI doesn’t just trust its first thought. The Verifier tests each lemma multiple times to get a “confidence score.” This reduces the chance that a wrong idea slips in and misleads the next steps.
- Final proof check: At the end, a strict process verifier reviews the whole solution and points out unclear or incorrect steps. The AI then revises the solution until it passes the check or runs out of attempts.
How it learns to improve (Reinforcement Learning)
The authors also train the AI with a method they call OREAL-H. In simple terms:
- The AI practices on hard problems.
- It gets feedback not only on whether the final answer is right, but also on the quality of its proof steps.
- It learns which lemmas are truly helpful by building a “map” (a dependency graph) that shows how small ideas lead to the final solution.
- Because the verifier can be a bit noisy (sometimes it passes so-so solutions just by luck), they use a smart way to turn repeated checks into a reliable confidence score—like estimating how trustworthy a coin’s fairness is after flipping it several times.
Main findings and why they matter
The results are strong:
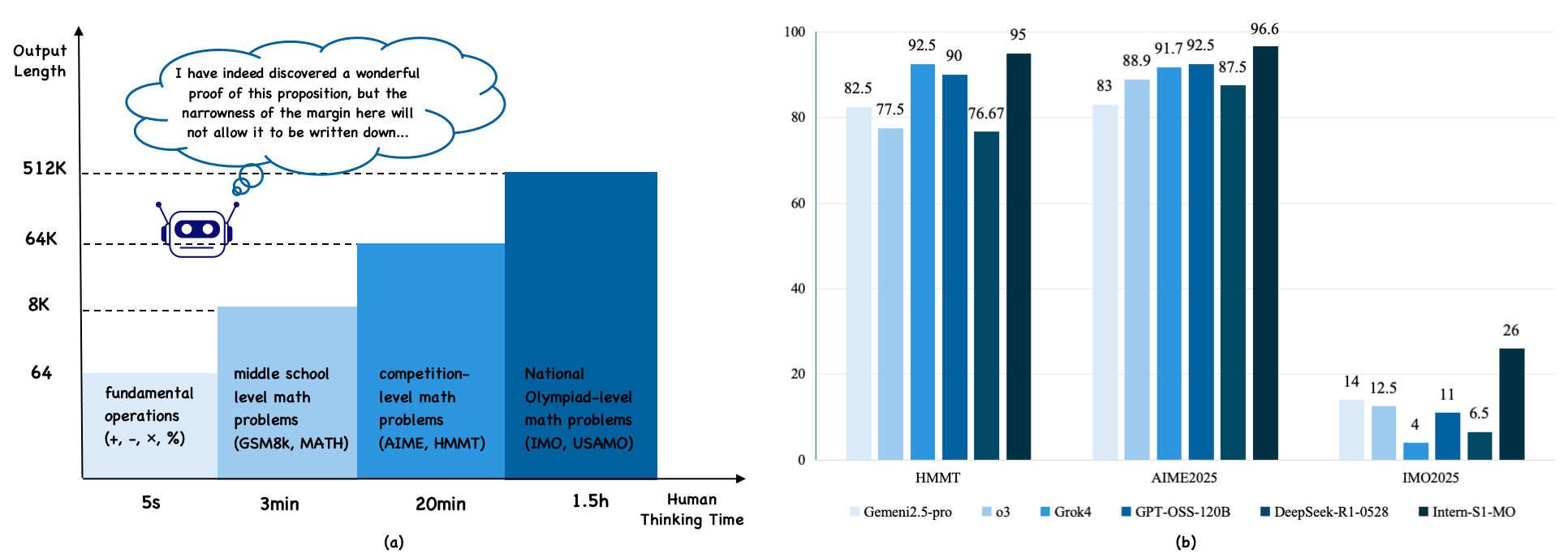
- On AIME 2025 and HMMT 2025, Intern-S1-MO scores about 96.6% and 95% on first attempts—better than other advanced models.
- On IMO 2025 (non-geometry problems), it earns 26 out of 35 points—similar to a human silver medalist.
- On CNMO 2025 (non-geometry), it scores 232.4 out of 260—state-of-the-art.
- In the real Chinese Mathematical Olympiad (CMO 2025), under official rules and human grading, it earns 102 out of 126—above the gold medal line.
Why this matters:
- The AI doesn’t just guess; it reasons step by step, keeps useful notes, and checks itself like a careful student.
- It can “think longer” effectively, even when it can’t fit everything into one giant memory window.
- It adapts its effort: it only uses many rounds and deep checking when problems are truly hard, saving time on easier ones.
What’s the impact?
This approach brings AI closer to how skilled humans solve tough math:
- It builds and reuses small truths (lemmas) over multiple rounds, just like mathematicians do.
- It verifies its logic, reducing the spread of errors.
- It learns from feedback about its process, not just from final answers.
Potential benefits:
- Better AI tutors that can explain and check long proofs step by step.
- Tools to assist researchers on complex problems by exploring, organizing, and verifying intermediate ideas.
- A path toward AI systems that can handle long-horizon reasoning in other fields (science, engineering, law) where careful, multi-step logic is essential.
In short, Intern-S1-MO shows that thoughtful planning, note-taking (lemmas), and rigorous checking let AI tackle Olympiad-level challenges—and that training it with rich feedback makes it even stronger over time.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, focused list of concrete gaps and unresolved questions that future work could address.
- Lemma memory design and scaling: How is the lemma library indexed, deduplicated, and pruned as it grows over many rounds and problems? What retrieval algorithms and metadata (assumptions, scope, dependencies) are needed to prevent drift, redundancy, and misuse of lemmas across contexts?
- Cross-problem knowledge reuse: Are lemmas reusable across different problems, or is memory strictly per-problem? Designing a global, reusable “theory” store and measuring its impact on generalization remains unexplored.
- Lemma representation fidelity: Lemmas are stored in natural language; how are implicit assumptions, quantifiers, and edge cases captured to avoid misapplication? A schema for formalizing lemma preconditions/postconditions is missing.
- Lemma verification calibration: Parallel sampling is used to assign confidence, but independence of samples and calibration of the resulting scores is unaddressed. How should thresholds be set, and how can false positives/negatives be systematically reduced?
- Non-local dependency verification: Verifying isolated lemmas may miss global proof constraints. Methods to detect non-local interactions, contradictory lemmas, or circular dependencies are not explored.
- Lemma dependency graph construction: The paper does not specify how natural-language lemmas are canonicalized, merged, or matched across rollouts to build graph nodes/edges. Algorithms for duplicate detection, conflict resolution, and graph quality measurement are needed.
- Value propagation in lemma graphs: The recursive definition of lemma value relies on successor sets, yet how successors are discovered, validated, and weighted is unclear. Empirical analysis of bias/variance in “optimistic max” value assignment is absent.
- High-level meta-policy learning: The hierarchical MDP introduces a high-level policy πH, but training and evaluation of meta-actions (e.g., when to summarize, verify, or commit) are not detailed. Comparing learned meta-policies against hand-crafted schedules would be instructive.
- Adaptive budget control: The claim of adaptive reasoning budget is not operationalized. A concrete policy for starting/stopping multi-round exploration, early exit criteria, and integration with budget-control RL (e.g., L1-type approaches) is missing.
- Reward model sensitivity: The conjugate Beta-Bernoulli reward uses n=4 PV trials; sensitivity analyses for n, priors, and discount γ are not reported. Are PV trials independent, and how does correlation affect posterior estimates and training stability?
- Alignment of PV signals with human grading: OPV’s F1>85% on ProcessBench does not guarantee alignment with competition grading rubrics. Quantifying PV-human agreement across domains and error types, and auditing PV failure modes on Olympiad proofs, is needed.
- Reward hacking risk: The agent may optimize for PV “passes” rather than mathematical correctness. Mechanisms to detect and prevent PV-specific exploitation (e.g., superficial plausibility) are not discussed.
- Efficiency and compute disclosure: The paper claims cost-effectiveness but does not report compute/time/energy per problem or training step. Publishing token budgets, wall-clock, and cost-per-point curves—matched against baselines—would clarify practical viability.
- Fairness in evaluation budgets: Benchmarks compare against scores from reports with unknown or different inference budgets and sampling strategies. Apples-to-apples evaluations with matched rounds, shots, and tokens are needed.
- Data contamination checks: With AoPS and in-house datasets used for cold start and RL, rigorous leak audits for AIME/HMMT/CNMO/IMO (including near-duplicates, solution exposure, and problem paraphrases) are not described.
- Geometry and multimodal reasoning: Geometry problems were excluded. Extending Intern-S1-MO to diagram understanding, geometric construction, and multimodal verification remains open.
- Formal verification bridge: The approach avoids formal proof systems, but a pathway to hybrid formal-nonformal verification (e.g., Lean/Isabelle integration) could provide stronger correctness guarantees; this is left unexplored.
- Termination criteria and diminishing returns: Multi-round reasoning and revision loops stop at a “maximum number of rounds,” but principled stopping rules, marginal utility estimates, and guarantees against unproductive exploration are not provided.
- Process-level metrics: Beyond pass@k, there are no quantitative metrics for lemma quality (precision/recall), coverage of sub-goals, or progress per round. Instrumentation for process-level evaluation and error taxonomy is lacking.
- Failure analysis: The paper notes remaining gaps on “spark-of-insight” problems but does not categorize failure modes (e.g., missing auxiliary constructions, non-standard transformations) or propose targeted interventions.
- Comparative search analyses: The lemma-graph surrogate to MCTS is claimed efficient, yet no head-to-head comparisons (quality, cost) against tree search baselines (ToT/MCTS variants) are reported.
- Reproducibility and release: Code, trained models, evaluation rubrics (for fine-grained grading), OPV/CompassVerifier configs, and seeds are not stated as released. Without them, replicability and external validation are difficult.
- Multi-agent orchestration details: Communication protocols, message schemas, and error-handling among reasoner/summarizer/verifier are not specified. Ablating single-model vs multi-agent pipelines and analyzing stability would inform design.
- Hyperparameter sensitivity: Number of rounds, shots, verifier calls, γ, and PV thresholds likely influence outcomes. Systematic sensitivity studies and guidelines for tuning are absent.
- Generalization beyond competitions: The system’s ability to tackle research-level proofs, novel theorem discovery, or cross-lingual/math-domain transfer (e.g., algebraic geometry, functional analysis) remains untested.
- Memory integrity over long horizons: Strategies for detecting and removing erroneous lemmas that slip through verification, managing conflicting entries, and preventing error propagation in extended sessions are not described.
- Single-attempt performance: IMO is reported with pass@4 and heavy test-time scaling; how does the agent perform under single-attempt constraints comparable to human contests (without multiple rollouts) is not shown.
Glossary
- AGI: A goal for broadly capable AI systems that can perform a wide range of intellectual tasks beyond narrow domains. Example: "which is regarded as a significant milestone towards AGI~\citep{sun2025survey}."
- Beta–Bernoulli conjugacy: A Bayesian relationship where a Beta prior with Bernoulli likelihood yields a Beta posterior, enabling closed-form updates from success/failure counts. Example: "the conjugate Beta-Bernoulli update yields the posterior:"
- Behavioral cloning: Supervised imitation of expert or successful trajectories to initialize a policy. Example: "we initialize policies via behavioural cloning on filtered trajectories"
- Chain-of-Thought (CoT): A prompting technique that elicits step-by-step reasoning traces to improve problem solving. Example: "Chain-of-Thought (CoT) \citep{Zhang2022AutomaticCO, Wang2023PlanandSolvePI}"
- CompassVerifier: An automated evaluator used to judge solution correctness in math tasks. Example: "then employ the CompassVerifier~\cite{liu2025compassverifier} and OPV~\citep{wu2025opv} as the judger for solution-based and proof-based questions, respectively."
- F1-score: The harmonic mean of precision and recall; a metric for evaluation performance. Example: "achieves an F1-score greater than 85\% on ProcessBench~\citep{zheng2024processbench}"
- Hierarchical Markov Decision Process (MDP): An MDP that models decision-making at multiple levels (high-level actions and low-level token generation). Example: "We model the agentic mathematical reasoning process as a Hierarchical Markov Decision Process"
- High-level critic: A value estimator at the meta-action level used for advantage computation in hierarchical RL. Example: "the per-round advantage can be estimated via a high-level critic "
- Lemma dependency graph: A graph capturing probabilistic contributions and dependencies among intermediate lemmas toward the final proof. Example: "we introduce a lemma dependency graph by aggregating reasoning states across multiple rollouts of the same problem."
- Lemma library: A structured repository of verified intermediate lemmas maintained across reasoning rounds to enable reuse. Example: "store them in a structured lemma library."
- Monte Carlo Tree Search (MCTS): A search algorithm that explores a tree of possible actions using randomized sampling and value estimates. Example: "a computationally efficient surrogate to Monte Carlo Tree Search (MCTS)"
- OREAL-H: A hierarchical RL framework extending OREAL to train multi-agent, multi-round mathematical reasoning. Example: "we additionally introduce the OREAL-H framework"
- Outcome Process Verifier (OPV): A verifier that produces process-level feedback signals by checking reasoning steps, used to guide training. Example: "OREAL-H exploits the additional reward signal produced by the outcome process verifier (OPV)"
- Outcome Reward Reinforcement Learning (OREAL): An RL paradigm that optimizes policies using sparse rewards based on final outcome correctness. Example: "Starting from the basic formulation of Outcome Reward Reinforcement Learning (OREAL) \citep{lyu2025exploring}"
- Pass@1: An accuracy metric measuring the probability that the top (first) generated solution is correct. Example: "use the unbiased pass@1~\citep{chen2021evaluating} as the metric"
- ProcessBench: A benchmark for evaluating process-level verification of reasoning steps. Example: "achieves an F1-score greater than 85\% on ProcessBench~\citep{zheng2024processbench}"
- Process Verifier (PV): A module that judges the logical rigor of proofs and provides granular feedback for RL training. Example: "we employ a Process Verifier (PV) to assess the logical rigor of complex mathematical proofs."
- Reinforcement Learning from Verifiable Rewards (RLVR): Training with rewards derived from verifiable signals (e.g., program checks), often beyond final outcomes. Example: "Reinforcement Learning from Verifiable Rewards (RLVR) \citep{Shao2024DeepSeekMathPT, Yue2025DoesRL, Zeng2025SimpleRLZooIA}."
- Temporal difference error: The difference between current value estimates and bootstrapped targets used to compute advantage in RL. Example: "The round-level advantage is then computed via the temporal difference error between the best potential of the current round and the next:"
- Test time scaling: Improving robustness by increasing inference-time computation (e.g., multiple verification runs). Example: "enhancing robustness through test time scaling by aggregating verification results across multiple runs"
- Tree-of-Thoughts: A reasoning framework that performs tree-structured exploration of solution paths. Example: "Tree-of-Thoughts \citep{Yao2023TreeOT}"
Practical Applications
Immediate Applications
Below is a concise set of deployable use cases grounded in the paper’s agent architecture (reasoner–summarizer–verifier), lemma-based memory, process verification (OPV), and the OREAL-H training framework.
- Math tutoring and olympiad training assistant (Education)
- What: Interactive tutor that guides students through multi-round, lemma-based problem solving; provides rigorous, verifier-backed feedback and partial-credit scoring.
- Tools/workflows: “Lemma Memory Engine” per student; OPV-in-the-loop feedback; fine-grained grading modeled after ProcessBench.
- Assumptions/dependencies: Access to a capable LRM; domain-appropriate verifier configurations; classroom integration and guardrails for correctness.
- Competition preparation and adjudication support (Education)
- What: Contest-grade solution drafting, self-reflection, and verification; support for tutor-led mock competitions; preliminary grading assistance for organizers (as demonstrated on CNMO/CMO).
- Tools/workflows: Test-time scaling orchestration; parallel verification pipelines; rubric-aligned partial credit.
- Assumptions/dependencies: Human-in-the-loop oversight; alignment with local grading standards; compute budgets for parallel runs.
- Auto-grading with process-aware feedback (Education/EdTech)
- What: Grade “show-your-work” mathematics assignments with step-level verification; allocate partial credit; flag reasoning gaps.
- Tools/workflows: OPV evaluator; lemma dependency graphs to map student steps to required subskills.
- Assumptions/dependencies: Reliable step segmentation in student solutions; school data privacy and compliance.
- Proof drafting and review assistant for mathematicians (Academia)
- What: Drafts, summarizes, and verifies natural-language proofs; maintains a reusable lemma library across drafts; highlights likely invalid steps with confidence.
- Tools/workflows: Lemma repository per project; multi-round refinement with OPV; confidence-weighted vetting.
- Assumptions/dependencies: Expert review; careful domain adaptation; versioning and provenance tracking.
- Content authoring and curation for math publishers (Publishing/Education)
- What: Generate high-quality problems and solutions; verifier-gated solution releases; curate thematic lemma collections.
- Tools/workflows: “Verifier-in-the-loop” authoring tools; structured lemma indexing and search.
- Assumptions/dependencies: Editorial QA; consistent verifier calibration; IP and licensing workflows.
- Auditable reasoning trails for LLM outputs (Policy/Compliance)
- What: Produce verifiable chains of reasoning with confidence scores; support audits and explainability for higher-stakes uses.
- Tools/workflows: Process-verifier middleware that attaches step confidence and error localization; lemma-based memory artifacts for traceability.
- Assumptions/dependencies: Sector-specific verification (finance, legal, healthcare) must be added; governance for storing reasoning traces.
- Adaptive compute budgeting in LLM reasoning (Software/MLOps)
- What: Automatically invoke multi-round exploration only for difficult queries; reduce costs for routine questions.
- Tools/workflows: Budget controller that monitors difficulty indicators and triggers hierarchical rounds; token usage dashboards.
- Assumptions/dependencies: Difficulty heuristics; acceptable latency; robust fallback for time constraints.
- Structured knowledge base construction from math corpora (Enterprise KM/Academia)
- What: Distill reusable lemmas from textbooks, papers, and solution repositories; maintain a confidence-scored library for reuse.
- Tools/workflows: Summarizer-verifier pipeline; lemma indexing; dependency graphs to expose prerequisite structure.
- Assumptions/dependencies: Quality of source materials; scalable storage and search; ongoing curation.
- Reasoning model training with process rewards (AI/ML Engineering)
- What: Apply OREAL-H to train LRMs using OPV-driven process feedback; stabilize learning with conjugate reward and lemma graphs.
- Tools/workflows: OREAL-H trainer; outcome/process verifiers; online trajectory harvesting.
- Assumptions/dependencies: Access to RL infrastructure and evaluators; curriculum design for complex problems; compute and monitoring.
- Early-stage code reasoning and algorithmic problem-solving (Software)
- What: Decompose algorithmic tasks into invariants/lemmas; verify stepwise derivations against tests; provide auditable reasoning during code reviews.
- Tools/workflows: Lemma memory for program invariants; test-based verifiers as process checks; multi-round refinement before merge.
- Assumptions/dependencies: Integration into CI/CD; domain-specific verification harnesses; developer oversight.
Long-Term Applications
These use cases require further research, scaling, domain-specific verifiers, or formal integration before broad deployment.
- Cross-domain long-horizon scientific assistant (Science/Research)
- What: Hypothesis generation, experiment planning, and multi-round inference with memory of partial results; verifier-guided refinement.
- Dependencies: Domain-specific process verifiers (statistics, lab safety); data integration; collaboration interfaces.
- Natural-language to formal proof bridging (Academia/Software)
- What: Map lemma repositories to Lean/Coq for mechanically checked proofs; use summarization to reduce formalization cost.
- Dependencies: Reliable translation from informal to formal; proof assistant integration; community acceptance.
- Clinical reasoning co-pilot (Healthcare)
- What: Differential diagnosis and guideline-concordant plans via lemma-based decomposition; process verification against medical knowledge bases.
- Dependencies: Medical-grade verifiers and evidence bases; regulatory approval; robust safety testing and auditability.
- Legal analysis and contract reasoning (Legal/Policy)
- What: Multi-round case law synthesis; lemma memory of precedents and clauses; verifier checks via citation consistency and rule compliance.
- Dependencies: High-fidelity legal verifiers; jurisdictional adaptation; explainability and risk management.
- Enterprise regulatory compliance automation (Finance/RegTech)
- What: Decompose complex regulations into reusable lemmas; verify controls and audit trails; generate regulator-ready reasoning reports.
- Dependencies: Sector-specific verification ontologies; integration with GRC systems; compliance sign-off.
- Large-scale software refactoring and codebase navigation (Software)
- What: Long-horizon planning of refactors; track invariants and dependencies as lemmas; iterative verification with tests and static analysis.
- Dependencies: Deep tooling integration; scalable analysis; organizational change management.
- Robotics task planning with verified subgoals (Robotics)
- What: Decompose tasks into verifiable subgoals; use conjugate rewards to handle noisy simulation/evaluators; roll out multi-round plans.
- Dependencies: High-fidelity simulators; safety constraints; real-world validation.
- Power grid and energy system planning (Energy)
- What: Multi-step optimization with constraints stored as lemmas; verification against operational and safety rules; scenario exploration.
- Dependencies: Domain models, simulators, constraint verifiers; regulator engagement.
- National-scale adaptive curriculum design and assessment (Policy/Education)
- What: Use lemma graphs to map prerequisite structures; generate personalized curricula and assessments with partial-credit schemes.
- Dependencies: Policy approval; fairness audits; infrastructure and teacher training.
- Standards for process-verifier–based AI evaluation (Policy/Standardization)
- What: Calibrate evaluators with conjugate reward; set benchmarks for process-level rigor beyond outcome-only scoring.
- Dependencies: Cross-industry consensus; reference datasets; governance for evaluator updates.
- Enterprise “lemma-first” knowledge management (Enterprise Software)
- What: Store reusable reasoning units across departments (risk, ops, R&D); enable compositional reuse at scale.
- Dependencies: Ontology design; interoperability across tools; curation practices.
- Continuous multi-agent research labs with online RL (Academia/Industry)
- What: Ongoing data collection and RL fine-tuning with process rewards; evolve reasoning agents in-the-loop with researchers.
- Dependencies: Significant compute; safety protocols; robust monitoring for drift and failure modes.
- Financial modeling and valuation co-pilots (Finance)
- What: Step-verified derivations of valuation models; lemma memory of assumptions; auditable scenario analyses.
- Dependencies: Domain verifiers (accounting, risk); governance; integration with existing analytics platforms.
- Explainable AI pipelines for high-stakes decisions (Government/Regulated Industries)
- What: Embed process verification and lemma memory to produce traceable, confidence-scored decisions.
- Dependencies: Sector-specific validators; legal frameworks for AI accountability; operational readiness.
Collections
Sign up for free to add this paper to one or more collections.
