Meta Flow Maps enable scalable reward alignment

Abstract: Controlling generative models is computationally expensive. This is because optimal alignment with a reward function--whether via inference-time steering or fine-tuning--requires estimating the value function. This task demands access to the conditional posterior $p_{1|t}(x_1|x_t)$, the distribution of clean data $x_1$ consistent with an intermediate state $x_t$, a requirement that typically compels methods to resort to costly trajectory simulations. To address this bottleneck, we introduce Meta Flow Maps (MFMs), a framework extending consistency models and flow maps into the stochastic regime. MFMs are trained to perform stochastic one-step posterior sampling, generating arbitrarily many i.i.d. draws of clean data $x_1$ from any intermediate state. Crucially, these samples provide a differentiable reparametrization that unlocks efficient value function estimation. We leverage this capability to solve bottlenecks in both paradigms: enabling inference-time steering without inner rollouts, and facilitating unbiased, off-policy fine-tuning to general rewards. Empirically, our single-particle steered-MFM sampler outperforms a Best-of-1000 baseline on ImageNet across multiple rewards at a fraction of the compute.

• The paper presents Meta Flow Maps that efficiently amortize the computation of conditional sampling for reward alignment in generative models.
• It introduces a unified approach combining inference-time steering and off-policy fine-tuning using unbiased gradient estimation and fixed-point regression.
• Empirical results show superior posterior sampling and reward metrics across benchmarks, significantly reducing computational cost.

Meta Flow Maps: Efficient and Scalable Reward Alignment for Generative Models

Introduction and Motivation

The paper "Meta Flow Maps enable scalable reward alignment" (2601.14430) addresses a central challenge in aligning high-dimensional generative models—specifically diffusion and flow-matching models—with arbitrary reward functions. Typical alignment strategies, such as inference-time steering and fine-tuning, require repeated, expensive posterior sampling via simulation (ODE/SDE rollouts) from conditional distributions defined by the generative process. This computational bottleneck fundamentally limits both the flexibility and scalability of alignment in practical settings, especially for large-scale datasets like ImageNet.

Meta Flow Maps (MFMs) are proposed as a novel architectural and algorithmic solution, designed to amortize the computational cost of conditional sampling by learning a stochastic operator that generates one-step, differentiable samples from the full family of relevant posterior distributions $p_{1|t}(x_1|x_t)$. This framework unifies and subsumes deterministic few-step generators, such as consistency models and flow maps, by introducing a stochastic mapping that preserves posterior diversity while enabling efficient Monte Carlo estimation of value function gradients required for optimal reward alignment.

Methodology

Conditional Transport and Optimal Control

Reward alignment is formalized as sampling from the reward-tilted distribution $$p_{\mathrm{reward}}(x) \propto p_{\mathrm{model}}(x) \exp(r(x))$$, with $r(x)$ an arbitrary reward. Both inference-time steering and fine-tuning can be expressed through the correction of generative trajectories using the gradient of a value function $$V_t(x_t) = \log \mathbb{E}_{X_1 | X_t = x_t}[\exp r(X_1)]$$. The key challenge is tractable, unbiased estimation of $\nabla V_t(x_t)$ at every step. Existing approaches rely on costly inner rollouts or make biased approximations of the posterior, both unsatisfactory in expressive, multimodal regimes.

Stochastic Flow Maps and Meta Flow Maps

MFMs generalize deterministic flow maps by introducing an exogenous noise source $\epsilon \sim p_0$ into the operator $X_{s,u}(\epsilon; t,x)$, resulting in stochastic maps that, for any context $(t,x)$, can efficiently sample from the full conditional $p_{1|t}(\cdot | x)$. The "meta" aspect denotes that a single neural operator amortizes over the infinite family of posteriors induced by all $(t,x)$ pairs, extracting the relevant flow dynamics from the generative base model and associating each context with its own stochastic transport.

Figure 1: MFM schema: conditioning on an intermediate time–state pair, the MFM learns a mapping from base noise to posterior endpoint samples, ensuring coverage over the entire conditional.

MFMs are parameterized using a residual formulation for flexible and stable training. Multiple possibilities are provided for the diagonal and consistency (self-distillation or teacher-guided) losses, inspired by established flow-matching and consistency objectives.

Integration with Reward Alignment Paradigms

MFMs support both inference-time steering via SDE/ODE simulation, using exact MC estimators for $\nabla V_t(x)$, and efficient off-policy fine-tuning to achieve permanent model alignment to rewards, through an unbiased fixed-point regression objective (MFM-FT). The framework ensures that the intractable "inner sample" step for posterior draws is replaced by a single MFM forward pass, crucial for scalability.

Empirical Results and Numerical Claims

Posterior Approximation and Guidance Tasks

MFMs are demonstrated initially on synthetic and low-dimensional settings (e.g., GMMs, MNIST), where ground-truth posteriors are available. MFMs outperform both heuristic steering methods (e.g., DPS) and particle-based approaches (e.g., SMC, TDS) according to statistical distances (Sliced Wasserstein, MMD) and control of mixture class ratios. Notably, MFMs recover the target posteriors nearly exactly with only a few Monte Carlo samples.

Figure 2: For GMM inverse problems, MFMs closely approximate the analytic posterior; MC convergence is observed with a small number of samples.

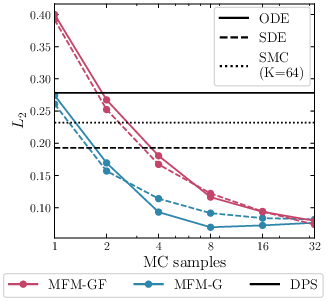
Figure 3: Comparison of empirical PMFs across classes for MNIST reward mixtures; MFMs correctly cover all modes as sampling increases, in contrast to heuristic approaches.

Scaling to High Dimensions and ImageNet

The stochastic posterior-matching capabilities of MFMs are validated on ImageNet at $256\times256$ resolution. Amortizing over the conditional family, MFMs achieve competitive or superior FID scores to strong deterministic flow map baselines (e.g., DMF/Mean Flow) for unconditional and conditional image generation, with the critical advantage of enabling efficient differentiable conditional sampling for reward-oriented applications.

Figure 4: MFM samples on ImageNet. (Left) Distributional diversity via posterior samples; (Right) Inference-time reward steering produces prompt-aligned images without retraining.

Reward Alignment and Inference-Time Steering Advantages

MFMs are evaluated for inference-time reward steering using large-scale text-to-image human preference rewards (ImageReward, PickScore, HPSv2). Both gradient-free (MFM-GF) and gradient-based (MFM-G) MC estimators produce sharp improvements in reward metrics over baselines such as DPS and Best-of-N.

MFMs display:

• Significantly higher reward attainment per compute unit: Even single-sample steering ($N=1$) outperforms Best-of-1000 search, with $100\times$ reduced NFE.
• No reward hacking: Score improvement generalizes between reward models, indicating robustness, not overfitting.
• Strong scaling properties: Quality of the steered generations and reward correlate positively with MC batch size.

  Figure 5: MFM-based steering achieves rewards unobtainable by standard baselines for multiple reward models.

  

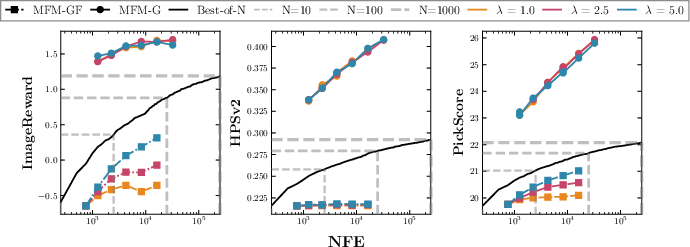
  Figure 6: Compute-normalized, MFMs offer consistently superior reward-per-NFE profiles compared to sample-selection baselines.

Fine-Tuning and Permanent Alignment

The MFM-FT objective allows for permanent, bias-free drift adaptation to reward-tilted targets in an entirely off-policy manner. Fine-tuned MFMs steadily increase all preference-aligned reward metrics during training, with qualitative improvements in sample quality and alignment across various reward weights.

Figure 7: Reward metrics during fine-tuning with HPSv2, demonstrating consistent improvements across all reward functions.

Figure 8: Generation samples before and after fine-tuning, showing increased photorealism and color, while maintaining class consistency.

Theoretical and Practical Implications

The principal theoretical contribution is the formalization and realization of amortized stochastic flow maps over infinite families of conditional transport problems. MFMs eliminate the need for nested, sample-inefficient rollouts at both training and inference time. This directly expands the practical feasibility of reward alignment strategies, including black-box reward alignment and complex downstream adaptation, to higher-dimensional and more complex problems.

MFMs unify inference-time and training-time reward alignment within a single, scalable architecture. The theoretical analysis shows explicit convergence rates for the effect of MC sample size and time discretization, highlighting both the statistical and computational trade-offs.

Limitations and Directions for Future Research

MFMs rely on the accurate neural parameterization of an operator over a much larger input space than traditional flow maps, potentially introducing capacity and generalization constraints as model and context complexity grow. As the underlying consistency and loss functions are modular, there is scope for exploiting architectural and training advances from flow map and consistency model research. Furthermore, extensions to arbitrary context families and stochastic processes suggest MFMs can support tasks beyond generative modeling, such as time-series posterior sampling and complex inverse problems.

Conclusion

Meta Flow Maps offer an efficient, modular framework for amortized conditional sampling in high-dimensional generative models, facilitating scalable and unbiased reward alignment at both inference and training time. Numerical evidence confirms strong sample quality, computational efficiency, and alignment control on challenging benchmarks. This work substantiates the feasibility of practical, scalable reward alignment for modern generative AI and opens new research directions into context-conditioned flow matching, generative model control, and amortized stochastic transport.