Flow Matching Policy Gradients (2507.21053v1)

Abstract: Flow-based generative models, including diffusion models, excel at modeling continuous distributions in high-dimensional spaces. In this work, we introduce Flow Policy Optimization (FPO), a simple on-policy reinforcement learning algorithm that brings flow matching into the policy gradient framework. FPO casts policy optimization as maximizing an advantage-weighted ratio computed from the conditional flow matching loss, in a manner compatible with the popular PPO-clip framework. It sidesteps the need for exact likelihood computation while preserving the generative capabilities of flow-based models. Unlike prior approaches for diffusion-based reinforcement learning that bind training to a specific sampling method, FPO is agnostic to the choice of diffusion or flow integration at both training and inference time. We show that FPO can train diffusion-style policies from scratch in a variety of continuous control tasks. We find that flow-based models can capture multimodal action distributions and achieve higher performance than Gaussian policies, particularly in under-conditioned settings.

• The paper presents a novel integration of flow-based generative models into policy gradients using a surrogate ratio derived from the conditional flow matching loss.
• It demonstrates superior performance over Gaussian policies in tasks such as GridWorld, continuous control, and under-conditioned humanoid control.
• The work highlights challenges like increased computational cost and instability in diffusion fine-tuning, setting directions for future research in efficient RL algorithms.

Flow Matching Policy Gradients: Integrating Flow-Based Generative Models with Policy Gradients

Flow Matching Policy Gradients (FPO) introduces a principled approach for integrating flow-based generative models, particularly diffusion models, into the policy gradient framework for reinforcement learning (RL). The method leverages the expressivity of flow models to capture complex, multimodal action distributions, while maintaining compatibility with standard on-policy RL algorithms such as Proximal Policy Optimization (PPO). This essay provides a technical summary of the FPO algorithm, its theoretical underpinnings, empirical results, and implications for future research in RL and generative modeling.

Motivation and Background

Traditional RL for continuous control predominantly employs Gaussian policies due to their tractability in likelihood computation and stable optimization. However, Gaussian policies are inherently limited in their ability to represent multimodal or highly non-Gaussian action distributions, which are often required in under-conditioned or ambiguous environments. Flow-based generative models, and in particular diffusion models, have demonstrated state-of-the-art performance in high-dimensional generative tasks across vision, audio, and robotics. Their integration into RL, however, has been hindered by the computational intractability of exact likelihood estimation and the complexity of adapting policy gradient methods to these models.

FPO addresses these challenges by reframing policy optimization as maximizing an advantage-weighted ratio derived from the conditional flow matching (CFM) loss, rather than explicit likelihoods. This approach sidesteps the need for exact likelihood computation, enabling the use of expressive flow-based policies within the PPO framework.

Flow Policy Optimization: Algorithmic Framework

FPO replaces the standard PPO likelihood ratio with a surrogate ratio based on the CFM loss. The core idea is to use the flow matching loss as a proxy for the log-likelihood in the policy gradient, leveraging the theoretical connection between the CFM loss and the evidence lower bound (ELBO) of the model.

The FPO surrogate ratio for a given action-observation pair is defined as:

$$\hat{r}^{\text{FPO}}(\theta) = \exp\left(\hat{\mathcal{L}}_{\text{CFM},\theta_{\text{old}}}(a_t; o_t) - \hat{\mathcal{L}}_{\text{CFM},\theta}(a_t; o_t)\right)$$

where $\hat{\mathcal{L}}_{\text{CFM},\theta}(a_t; o_t)$ is a Monte Carlo estimate of the per-sample CFM loss, computed over sampled noise and flow timesteps.

This ratio is then used in the PPO-style clipped objective:

$$\max_\theta \ \mathbb{E}_{a_t \sim \pi_\theta(a_t|o_t)} \left[ \min \left( \hat{r}^{\text{FPO}}(\theta) \hat{A}_t, \, \text{clip}(\hat{r}^{\text{FPO}}(\theta), 1 - \epsilon, 1 + \epsilon) \hat{A}_t \right) \right]$$

where $\hat{A}_t$ is the estimated advantage.

The FPO algorithm is agnostic to the choice of flow or diffusion sampler, allowing for flexible integration with deterministic or stochastic sampling, and any number of integration steps during training or inference.

Theoretical Analysis

FPO's surrogate ratio is theoretically justified by the equivalence between the weighted denoising loss (used in flow matching) and the negative ELBO, as established in prior work. For monotonic weighting functions, minimizing the CFM loss is equivalent to maximizing the expected ELBO of noise-perturbed data. In the special case of uniform weighting (standard diffusion), the loss directly corresponds to maximizing the ELBO of clean actions.

The FPO ratio thus decomposes into the standard likelihood ratio and an inverse KL gap correction, ensuring that optimization increases the modeled likelihood of high-advantage actions while tightening the approximation to the true log-likelihood.

Empirical Evaluation

FPO is evaluated across a spectrum of RL tasks, including a multimodal GridWorld, continuous control in MuJoCo Playground, and high-dimensional humanoid control in Isaac Gym.

Multimodal GridWorld

FPO demonstrates the ability to learn policies with genuinely multimodal action distributions in environments with multiple optimal solutions. At saddle points, the learned flow transforms Gaussian noise into a bimodal distribution, enabling the agent to reach different goals from the same initial state.

Figure 1: FPO-trained policy in GridWorld, showing denoised actions (left), flow evolution at a saddle point (center), and diverse sampled trajectories (right) illustrating multimodal behavior.

In contrast, Gaussian policies trained with PPO exhibit deterministic behavior, consistently selecting the nearest goal and lacking trajectory diversity.

Continuous Control: MuJoCo Playground

FPO is compared against Gaussian PPO and DPPO (a diffusion-based PPO variant) on 10 continuous control tasks. FPO outperforms both baselines in 8 out of 10 tasks, achieving higher average evaluation rewards and demonstrating superior learning efficiency, especially as the number of Monte Carlo samples for the CFM loss increases.

Figure 2: FPO vs. Gaussian PPO on DM Control Suite tasks, showing mean evaluation reward and standard error over 60M environment steps.

Ablation studies reveal that:

• Increasing the number of $(\tau, \epsilon)$ samples improves performance.
• Using $\epsilon$-MSE (noise prediction) for the flow matching loss yields better generalization than velocity-based losses.
• The choice of PPO clipping parameter $\epsilon$ significantly affects stability and final performance.

High-Dimensional Humanoid Control

FPO is applied to physics-based humanoid control with varying levels of goal conditioning (full joints, root+hands, root only). While both FPO and Gaussian PPO perform comparably under full conditioning, FPO significantly outperforms Gaussian PPO in under-conditioned settings, achieving higher success rates, longer alive durations, and lower mean per-joint position error (MPJPE).

Figure 3: Episode return during training for humanoid control, with FPO matching or exceeding Gaussian PPO, especially under sparse goal conditioning.

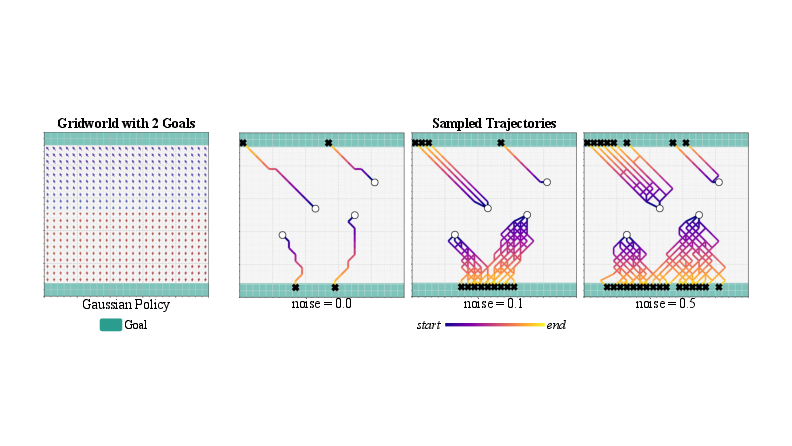
Figure 4: Visualization of humanoid tracking in the root+hands setting, with FPO closely following the reference motion while Gaussian PPO fails.

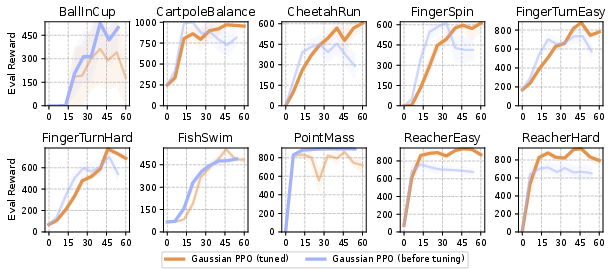
Figure 5: FPO enables robust locomotion across rough terrain via terrain randomization.

These results highlight the practical advantage of flow-based policies in capturing the complex, multimodal action distributions required for under-conditioned control.

Limitations and Negative Results

While FPO enables expressive policy learning, it incurs higher computational cost compared to Gaussian policies due to the complexity of flow-based models. Additionally, FPO lacks established mechanisms for adaptive learning rate adjustment and entropy regularization based on KL divergence estimation.

Attempts to apply FPO for RL fine-tuning of pre-trained image diffusion models (e.g., Stable Diffusion) revealed instability, particularly due to the compounding effects of classifier-free guidance (CFG) and self-generated data. Both low and high CFG scales led to divergence and degradation of image quality over training epochs, consistent with known challenges in self-training of generative models.

Figure 6: Image generation during FPO fine-tuning of Stable Diffusion, showing quality regression and divergence under different CFG scales.

Implications and Future Directions

FPO provides a general and practical framework for integrating flow-based generative models into on-policy RL. Its ability to model complex, multimodal action distributions opens new possibilities for RL in under-conditioned, ambiguous, or high-dimensional environments. The method's compatibility with standard PPO infrastructure facilitates adoption and experimentation.

Future research directions include:

• Developing efficient approximations or regularization techniques to reduce the computational overhead of flow-based policies.
• Extending FPO to off-policy settings and large-scale pretraining/fine-tuning scenarios.
• Investigating robust strategies for RL fine-tuning of diffusion models in generative tasks, addressing the instability observed in self-training regimes.
• Exploring the use of FPO in sim-to-real transfer, where the expressivity of flow-based policies may bridge the gap between simulation and real-world deployment.

Conclusion

Flow Matching Policy Gradients (FPO) establishes a theoretically sound and empirically validated approach for training flow-based generative policies via policy gradients. By leveraging the conditional flow matching loss as a surrogate for likelihood, FPO enables expressive, multimodal policy learning within the stable and efficient PPO framework. The method demonstrates clear advantages in tasks requiring complex action distributions, particularly in under-conditioned control, and provides a foundation for future advances in RL with generative models.