Test-time scaling of diffusions with flow maps (2511.22688v1)
Abstract: A common recipe to improve diffusion models at test-time so that samples score highly against a user-specified reward is to introduce the gradient of the reward into the dynamics of the diffusion itself. This procedure is often ill posed, as user-specified rewards are usually only well defined on the data distribution at the end of generation. While common workarounds to this problem are to use a denoiser to estimate what a sample would have been at the end of generation, we propose a simple solution to this problem by working directly with a flow map. By exploiting a relationship between the flow map and velocity field governing the instantaneous transport, we construct an algorithm, Flow Map Trajectory Tilting (FMTT), which provably performs better ascent on the reward than standard test-time methods involving the gradient of the reward. The approach can be used to either perform exact sampling via importance weighting or principled search that identifies local maximizers of the reward-tilted distribution. We demonstrate the efficacy of our approach against other look-ahead techniques, and show how the flow map enables engagement with complicated reward functions that make possible new forms of image editing, e.g. by interfacing with vision LLMs.
Sponsor
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper is about making image generators (like the models behind popular AI art tools) follow a user’s wishes more closely at the moment of generation without retraining the model. The authors introduce a method called Flow Map Trajectory Tilting (FMTT), which uses a “look-ahead” tool to peek at where a generation is heading and steer it toward higher scores on a chosen “reward” (for example: “Does the image show a clock at exactly 3:45?” or “Is the image symmetric?”). They show this makes guidance smarter, more reliable, and sometimes even exact in a mathematical sense.
Key Objectives and Questions
The paper asks:
- How can we guide a diffusion model during generation so its outputs better match a user’s reward (goal) without retraining?
- Can we use a flow map—a function that jumps directly from one time to another—to properly “look ahead” and get a useful reward signal early in the process?
- Can we adjust the math so that the guided samples still represent the right, reward-tilted distribution, not just “good-looking” but biased samples?
- Can this approach scale well (improve as we spend more compute), and work with complex rewards—like those coming from Vision-LLMs (VLMs) that judge images using natural language?
Methods and Ideas (with simple explanations)
Diffusion models and the problem with rewards
- Think of image generation as slowly transforming noise into a clear picture over time, like focusing a blurry photo step by step.
- A “reward” is a score function that says how good the final image is for your goal. Most rewards are meaningful only at the end (when the image is clear), not halfway through when it’s noisy.
- A common trick is to push the generation toward higher rewards using the reward’s gradient (like climbing uphill). But that breaks down early in the process because the image isn’t clear yet—and the reward isn’t informative.
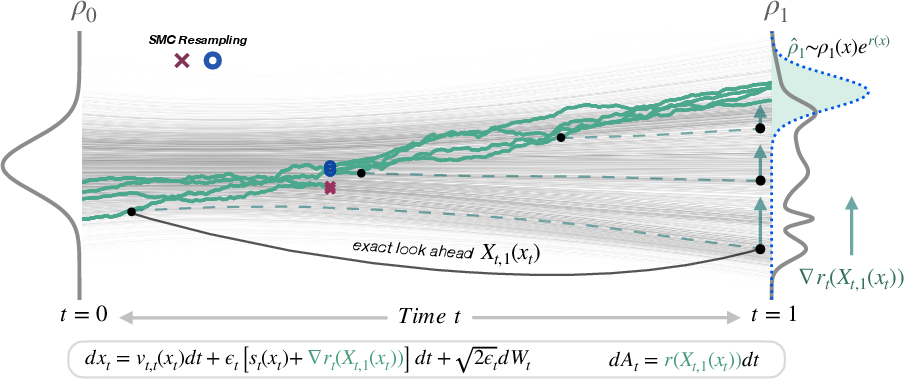
Flow maps: a better “look-ahead”
- A flow map is a function that jumps you from a current time to a future time in the generation, like skipping ahead in a video.
- Instead of guessing what the final image will be using a one-step “denoiser” (a rough, blurry predictor), the flow map can quickly predict the final image much more accurately.
- FMTT uses : given the current state at time , it looks ahead to what the final image would be at time 1. Then it computes the reward on that looked-ahead image. This gives useful guidance even at early timesteps.
Making guidance both effective and correct
- Just adding reward gradients changes the generation, but doesn’t guarantee you’re sampling the true “reward-tilted” distribution (the mathematically correct version of “favor high-reward images”).
- The authors fix this using importance weighting: as you generate, you also track a simple weight that corrects for the guidance. Intuitively, gives extra credit to samples that the guidance pushed in a useful way, so averages stay unbiased.
- With the flow map look-ahead, this weight becomes especially simple:
- Translation: throughout the trajectory, add up the reward of the looked-ahead image. This is easy to compute and uses the full look-ahead signal.
Sampling vs. search
- You can use these weights for exact sampling (so outputs truly represent the reward-tilted distribution) via Sequential Monte Carlo (SMC), or you can do “search”: keep the best candidates as you go to find high-reward images quickly.
- The method also introduces a way to adjust the model’s “drift” (its main direction of change) using the reward, which can further help guidance—still with a correction that keeps sampling unbiased.
Measuring efficiency: thermodynamic length
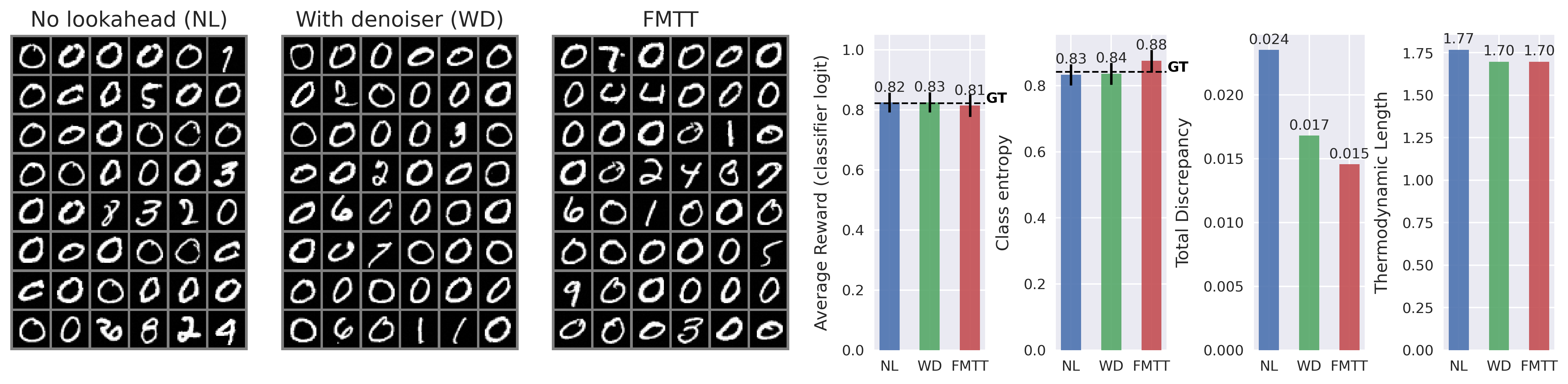
- The paper introduces a practical diagnostic called thermodynamic length: a number you can compute during generation that indicates how efficiently your guidance is sampling the tilted distribution.
- Shorter thermodynamic length means your guidance is working better with less variance and fewer wasted samples.
Main Findings and Why They Matter
- FMTT uses the flow map’s look-ahead to provide strong, meaningful reward gradients at every step. This greatly improves steering compared to using a denoiser look-ahead, especially early on when images are still blurry.
- The importance weights become simple and stable when using flow maps, enabling both:
- Exact sampling of the reward-tilted distribution
- Practical search strategies for high-reward outputs
- Experiments:
- MNIST (handwritten digits): When tilting an unconditional generator toward a specific class (e.g., zeros), FMTT shows lower thermodynamic length and better efficiency compared to baselines.
- Text-to-image with a 4-step flow map distilled from a strong diffusion model (FLUX.1-dev):
- Human preference rewards: modest gains because the base model is already trained toward such preferences. Even so, FMTT provides the best or near-best performance and good compute efficiency.
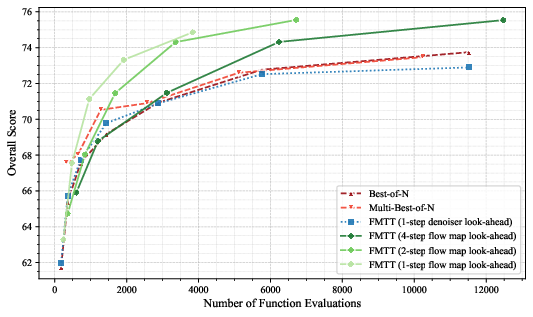
- Geometric rewards (like symmetry, anti-symmetry, rotation invariance, or masking): FMTT beats methods like Best-of-N, Multi-Best-of-N, and ReNO. It produces sharper images that follow the constraints more reliably—even for hard cases like masked content placement.
- VLM rewards (natural language judges): On UniGenBench++, FMTT scales better than Best-of-N and Multi-Best-of-N. The 1-step denoiser look-ahead often fails to improve over Best-of-N, but the flow map look-ahead consistently helps—because its predictions are meaningful even at high noise.
In short: FMTT makes test-time guidance both smarter and more principled. It handles complex, nuanced rewards (including natural-language ones from VLMs) and can either do exact sampling or efficient search.
Implications and Impact
- Better control over image generation: FMTT helps models follow detailed instructions and complex rules, like precise layouts, symmetry, or text alignment, without retraining.
- Natural-language rewards via VLMs: You can ask a model to “make an image matching this caption” and use the VLM’s yes/no score as the reward. FMTT makes that kind of guidance practical and effective.
- Reliable scaling: As you spend more compute at test time, FMTT gets better in a predictable way, making it useful for applications that need high accuracy without retraining.
- Scientific correctness when needed: Because FMTT includes importance weighting, it can produce samples that truly represent the mathematically correct reward-tilted distribution, not just “good-looking” results.
- Caution: Reward hacking is possible—if the reward is poorly defined, the search might exploit loopholes. Careful reward design helps avoid this.
Overall, FMTT shows how combining flow maps (for look-ahead) with principled weighting can significantly improve test-time guidance for diffusions—making them more controllable, efficient, and compatible with advanced reward functions.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, concrete list of what remains missing, uncertain, or unexplored in the paper—each item framed to guide future research.
- Formalize the “thermodynamic length” claim: provide rigorous derivations linking thermodynamic length to SMC variance, with tight bounds and practical estimators; validate how it predicts efficiency across schedules, particle counts, and resampling strategies.
- Quantify bias from approximate flow maps: analyze how errors in learned flow maps X_{t,1} propagate to reward look-ahead, importance weights A_t, and final sampling/search outcomes; derive conditions under which FMTT remains unbiased or approximately correct.
- Characterize finite-step discretization error: provide convergence rates and bias quantification for time discretization, stochastic noise, and resampling in high dimensions; paper sensitivity to K (steps), N (particles), and resampling frequency.
- Optimize reward annealing schedules r_t(x): explore alternatives to r_t(x)=t·r(X_{t,1}(x)) that minimize thermodynamic length or variance; derive principled schedule design criteria and adaptive schemes.
- Tune ε_t and χ_t effectively: establish guidelines for diffusion strength ε_t and drift augmentation χ_t schedules to balance reward ascent, stability, and diversity; paper robustness across tasks and models.
- Efficient computation of ∆r_t and inner products in dÃ_t: develop scalable approximations (e.g., Hutchinson trace, low-rank/spectral methods) for Laplacian and second-order terms in high-dimensional image spaces, with error controls.
- Measure look-ahead fidelity across time: systematically evaluate flow map look-ahead quality at early/high-noise timesteps vs denoiser-based look-ahead; determine thresholds where flow maps meaningfully improve reward gradients.
- Quantify “out-of-support” exploration: measure how FMTT moves outside the base model’s support, its impact on realism and artifacts, and trade-offs with diversity; introduce diagnostics (e.g., classifier support metrics, image quality scores).
- Demonstrate exact tilted sampling at scale: extend unbiased sampling experiments beyond MNIST to large text-to-image models; report effective sample size, variance of normalization estimates, and accuracy of partition function estimates.
- Develop adaptive SMC for FMTT: design resampling schedules driven by ESS or thermodynamic length; evaluate their benefits in reducing variance and computational cost in high-dimensional settings.
- Robustness to reward hacking with VLMs: move beyond prompt engineering to formal defenses (e.g., consistency checks, adversarial testing, multi-judge ensembles); quantify exploitation risks and mitigation efficacy.
- Clarify differentiability of VLM rewards: assess gradient availability and quality (noise, bias) for the chosen VLMs; provide methods for non-differentiable rewards (e.g., REINFORCE, score-function estimators, surrogate smoothing).
- Compute and memory profiling: benchmark the cost of flow map look-ahead and reward backprop; characterize scalability across GPUs, batch sizes, and model sizes, including memory pressure during backward passes.
- Extend to other modalities: adapt FMTT to audio, video, 3D, and discrete/autoregressive generative models; address modality-specific challenges (e.g., temporal consistency, discrete gradients).
- Compare to nested look-ahead baselines: evaluate against per-step inner solves that predict terminal states more accurately than denoisers, at matched compute; quantify trade-offs between accuracy and cost.
- Sensitivity to base model and distillation quality: test FMTT across diverse diffusion/flow architectures, training regimes, and step counts; analyze how distillation errors affect FMTT’s performance.
- Maintain diversity under search: directly measure diversity collapse for gradient-based/top-n search; propose mechanisms (e.g., entropy regularization, diversity-aware resampling) to preserve variety while optimizing rewards.
- Calibrate and audit VLM judges: paper biases and calibration of reward models across prompts and demographics; develop calibration procedures that stabilize reward landscapes and reduce unintended bias.
- Convergence guarantees for search: analyze the optimization dynamics induced by FMTT; provide conditions under which local maximizers of the reward-tilted distribution are found or escaped.
- High-dimensional partition function estimation: develop practical, accurate estimators and confidence intervals for tilted normalization constants in T2I tasks; validate diagnostics for estimator reliability.
- Differentiable approximations for non-smooth transforms: when rewards involve masking or discrete rotations, propose differentiable surrogates and quantify their effect on gradients, stability, and final outputs.
- Optimal look-ahead depth selection: paper the trade-off between single-step, few-step, and full-step flow map look-ahead; design adaptive depth policies informed by gradient signal or thermodynamic diagnostics.
- Sensitivity to noise schedules: evaluate different ε_t schedules (linear, cosine, learned) and their effect on reward alignment, stability, and sample quality; identify schedules that minimize thermodynamic length.
- Safety and content guardrails: when rewards incentivize OOD content, analyze safety risks and propose guardrails (e.g., content filters, secondary constraints) integrated into the search/sampling process.
Glossary
- Birth/death processes: Continuous-time stochastic mechanisms that add or remove particles in a sampling population to maintain distributional targets. "as is done in Sequential Monte Carlo (SMC) and birth/death processes, as is depicted in Figure \ref{fig:overview}."
- Brownian motion: A continuous-time random process with independent Gaussian increments used to model noise in SDEs. "where is an arbitrarily tunable diffusion coefficient and is an incremental Brownian motion~\citep{albergo2023stochastic}."
- Continuity equation: A partial differential equation describing conservation of probability mass under a velocity field. "Since the time dependent PDF of the solutions to \eqref{eq:ode} at time satisfies the continuity equation"
- Coupling: A joint distribution over variables whose marginals match specified target distributions, used to define interpolants. "where is some coupling from which are drawn that marginalizes onto , "
- Denoiser: A learned function that estimates a clean sample at the end of generation from a noisy intermediate state. "the denoiser "
- Diffeomorphism: A smooth, invertible mapping with a smooth inverse, transporting samples between distributions. "are mapped via a diffeomorphism to samples "
- Drift: The deterministic component of a differential equation governing the direction and rate of change of states. "learns the solution operator of a probability flow ODE directly rather than the associated drift~\citep{boffi_flow_2024,boffi2025build,Sabour2025AlignYF, geng2025mean}."
- Eulerian equation: A PDE characterizing how a flow map evolves with respect to time and space under a velocity field. "Importantly, the flow map satisfies the Eulerian equation"
- Fokker-Planck equation: A PDE describing the time evolution of the probability density of a stochastic process. "the PDF of \eqref{eq:sde} satisfies the Fokker-Planck equation"
- Flow-based generative modeling: Methods that generate data by learning transport maps or dynamics that transform a base distribution into a target one. "flow-based generative modeling that learns the solution operator of a probability flow ODE directly rather than the associated drift~"
- Flow map: The two-time mapping that transports a state from time s to time t along learned dynamics. "Associated with these dynamics is the two-time flow map "
- Implicit flow: A formulation where the flow is defined through identities relating the map to the underlying velocity without explicit integration. "we show that an implicit flow can be used to define a reward-guided generative process"
- Importance weights: Scalar weights used to correct bias in modified dynamics or to perform exact sampling via reweighting. "we show that the importance weights for this Jarzynski/SMC scheme reduce to a remarkably simple formula."
- Jarzynski equality: A non-equilibrium statistical physics identity used to relate expectations under modified dynamics to target distributions via exponential reweighting. "coming from an adaptation of the Jarzynski equality \citep{jarzynski1997, vaikuntanathan2008}:"
- Jarzynski's estimator: The practical reweighting estimator derived from the Jarzynski equality for unbiased expectation computation. "Jarzynski's estimator"
- Look-ahead map: A function that predicts the terminal point of a trajectory from its current state, enabling reward evaluation during generation. "Using the look-ahead map in the diffusion inside the reward"
- Probability density function (PDF): A function that describes the relative likelihood of a random variable taking given values. "probability density function (PDF) "
- Probability flow ODE: A deterministic ODE whose solution preserves the marginal distributions of a corresponding stochastic process. "learns the solution operator of a probability flow ODE directly"
- Resampling: A selection procedure in particle methods that duplicates high-weight trajectories and removes low-weight ones to control variance. "the walkers can be resampled using the importance weights, removing some and duplicating others."
- Score function: The gradient of the log-density, used to guide stochastic dynamics and relate to the velocity field in interpolant models. "By Stein's identity, the score is given by "
- Sequential Monte Carlo (SMC): A class of particle-based algorithms that approximate evolving distributions via propagation and resampling. "as is done in Sequential Monte Carlo (SMC)"
- Stein's identity: A probabilistic identity connecting expectations under a distribution to derivatives, useful for deriving score relations. "By Stein's identity, the score is given by "
- Stochastic differential equation (SDE): A differential equation including random noise terms that models stochastic dynamics. "numerically solving an ordinary or stochastic differential equation (ODE/SDE)"
- Stochastic interpolants: Time-dependent stochastic processes that connect base and target distributions for training transport dynamics. "A common strategy to construct such a path and regress is that of stochastic interpolants \citep{albergo2022building, albergo2023stochastic, lipman2022flow, liu2022flow}"
- Tangent identity: A relation stating that the time derivative of the flow map at equal times equals the velocity field. "via the tangent identity~\citep{kim_consistency_2024,boffi2025build}"
- Thermodynamic length: A path-dependent metric of sampling efficiency and discrepancy accumulation along a tilted process. "a measure of the efficiency of the guidance in sampling the tilted distribution."
- Tilted distribution: A target distribution reweighted by a reward function to favor high-reward samples. "sampling the tilted distribution."
- Total discrepancy: A computable quantity summarizing cumulative mismatch between proposal and target across a schedule in SMC. "the total discrepancy "
- Velocity field: A time-dependent vector field that determines the instantaneous transport of probability mass. "velocity field "
- Vision-LLMs (VLMs): Models that jointly process images and text to perform tasks like scoring alignment or answering queries. "vision-LLMs (VLMs)"
Practical Applications
Immediate Applications
The following items can be implemented with current diffusion/flow-map models and off-the-shelf reward models (including VLMs), using the paper’s Flow Map Trajectory Tilting (FMTT) algorithm, importance weighting (Jarzynski/SMC), and search variants.
- Production-grade text-to-image alignment with natural-language rewards
- Sector: software, creative industries, advertising, e-commerce
- Application: Add FMTT as an inference-time alignment layer to existing text-to-image systems (e.g., FLUX-derived, Align-Your-Flow-distilled flow maps) to reliably render precise attributes (e.g., legible text, specific clock times, object positions), using VLMs as judges (“Is PROMPT a correct caption for the image?”).
- Tools/workflows:
- FMTT plugin that composes reward r(X_{t,1}(x)) via flow-map look-ahead
- Top‑n or beam search with reward gradients, backed by SMC if exact sampling is needed
- VLM reward adapter (binary yes/no scoring) and “reward template” authoring
- Assumptions/dependencies: Access to a flow-map sampler (e.g., 4-step distilled model), differentiable reward model or surrogate gradients, GPU budget for reward forward/gradients; careful prompt engineering to avoid reward hacking.
- Constraint-driven image editing (masking, symmetry, rotation invariance)
- Sector: design tools, product photography, e‑commerce, game assets
- Application: Use geometric rewards r(x)=−d(x, T(x)) and masked-region rewards to force content layout (e.g., keep content only in unmasked areas; enforce bilateral symmetry, anti‑symmetry, rotation invariance) for catalog images, logos, UI mockups, or stylized scenes.
- Tools/workflows:
- Geometry/mask reward library and differentiable distance metrics
- FMTT gradient-based tilting of the generative dynamics (flow-map look-ahead)
- Top‑n sampling for selection without retraining
- Assumptions/dependencies: Reward must be meaningful at the terminal state; flow-map look-ahead ensures early-time signal; denoiser-only look-ahead is insufficient for hard constraints.
- Preference optimization at inference without retraining
- Sector: model operations (MLOps), A/B testing, content platforms
- Application: Combine multiple human preference rewards (PickScore, HPSv2, ImageReward, CLIPScore) and apply FMTT to incrementally improve alignment and visual quality without fine-tuning, maintaining diversity via SMC resampling.
- Tools/workflows:
- Reward aggregator and scheduler
- Compute-aware search (thermodynamic length as a diagnostic to choose schedule)
- Assumptions/dependencies: Base models already post-trained on preference data; improvements are incremental but robust when constraint rewards are specialized.
- Multi-image matching and brand/style compliance
- Sector: e‑commerce, marketing, creative ops
- Application: VLM rewards that compare a generated image to reference images (brand palette, layout grids, product placement), ensuring compliance (e.g., “Does the image match brand guidelines?”).
- Tools/workflows:
- Multi-image VLM judge integration (e.g., Qwen2.5‑VL for multi-image scoring)
- Flow-map FMTT search with guardrail prompts and audit logs
- Assumptions/dependencies: VLM reliability and bias; reward hacking mitigation via carefully crafted questions; periodic human review.
- Exact sampling of reward-tilted distributions for research and benchmarking
- Sector: academia, scientific computing
- Application: Use FMTT with Jarzynski/SMC importance weights A_t=∫₀ᵗ r(X_{s,1}(x_s))ds to exactly sample ρ̂_t ∝ ρ_t e{r_t}, enabling principled studies of tilted generative paths (e.g., class-conditional MNIST from an unconditional model).
- Tools/workflows:
- SMC sampler with flow-map look-ahead
- Estimation of normalization constants and uncertainty via importance weights
- Assumptions/dependencies: Well-calibrated flow-map and score models; sufficient particle count; schedule discretization accuracy.
- Thermodynamic length as a practical efficiency diagnostic
- Sector: academia, MLOps
- Application: Monitor thermodynamic length to tune schedules and resampling frequency in SMC/top‑n pipelines; use it as a proxy for variance/efficiency when optimizing reward-guided sampling.
- Tools/workflows:
- Dashboard to visualize thermodynamic length and total discrepancy
- Auto‑tuning of step counts and resampling triggers
- Assumptions/dependencies: Reliable computation of length from A_t updates; consistency across prompts and datasets.
- Trust & Safety guardrails via reward tilting
- Sector: policy, platform safety
- Application: Add safety rewards (e.g., disallow unsafe content, ensure legible disclaimers) at inference-time without retraining; resample or steer generation away from policy-violating regions.
- Tools/workflows:
- Safety reward suites (VLM moderation prompts + image classifiers)
- FMTT steering plus SMC-based rejection/resampling
- Assumptions/dependencies: Robust safety rewards (ensemble judges), safeguards against reward hacking; auditing and retention policies.
- Synthetic data generation with strict programmatic constraints
- Sector: computer vision, ML data ops
- Application: Generate curated datasets for detection and layout tasks (e.g., controlled symmetry, masks, color counts, object bindings) to augment training with high-precision synthetic labels.
- Tools/workflows:
- Programmatic reward specs for scene constraints
- Batch FMTT pipelines with metadata export
- Assumptions/dependencies: Reward correctness and generalization to real distributions; evaluation of domain gap.
- Compute-performance optimization of search strategies
- Sector: software engineering for AI systems
- Application: Replace expensive multi-best‑of‑N searches with FMTT gradient-based look-ahead; achieve better scores at lower NFEs on benchmarks like UniGenBench++.
- Tools/workflows:
- Hybrid search (beam + FMTT gradients)
- NFE budgeting and dynamic schedule selection
- Assumptions/dependencies: Flow-map availability; reward models’ throughput; careful NFE accounting.
Long-Term Applications
These require further research, domain-specific modeling, reliable reward functions, scaling, or standardization before broad deployment.
- Cross‑modal generative control (video, audio, 3D, CAD)
- Sector: media, gaming, design, AR/VR
- Application: Extend FMTT to flow-map models for video/audio/3D, enforcing temporal or physical constraints (e.g., motion continuity, rotation invariance across frames).
- Tools/workflows: Flow-map training for new modalities; differentiable, domain-specific reward functions.
- Assumptions/dependencies: Availability of accurate flow maps beyond images; scalable reward gradients in high dimensions.
- Inverse design in science and engineering
- Sector: materials science, chemistry, biotech
- Application: Use FMTT as an exact or approximate sampler for reward-tilted distributions that encode desired properties (e.g., stability, bandgaps, binding affinities); bias generative models toward candidate designs.
- Tools/workflows: Property predictors with reliable gradients; SMC with importance weights for exact sampling; constraint libraries.
- Assumptions/dependencies: High-fidelity generative models for domain data; validated property/reward models; regulatory considerations in biotech.
- Rare-event and tail-risk simulation
- Sector: finance, insurance, climate risk
- Application: Improved importance sampling via flow-map look-ahead to tilt toward rare but critical events; estimate tail probabilities with lower variance.
- Tools/workflows: Flow-map generative surrogates for stochastic processes; SMC/Jarzynski estimators; thermodynamic length planning.
- Assumptions/dependencies: Domain-appropriate generative surrogates; reward definitions for extreme events; rigorous validation.
- Diffusion-based planning and control in robotics
- Sector: robotics, autonomy
- Application: Apply FMTT to diffusion planners, tilting trajectories toward constraints (safety margins, energy limits, timing) with look-ahead; potentially integrate with model-predictive control.
- Tools/workflows: Robotics diffusion models with flow maps; physics-informed rewards; real-time schedulers.
- Assumptions/dependencies: Real-time compute feasibility; reliable gradients under sensor uncertainty; safety certifications.
- Policy-grade guardrail engines with formalized “reward templates”
- Sector: policy, platform governance
- Application: Standardize reward prompt templates for moderation, transparency, and fairness; certify inference-time alignment modules; audit thermodynamic length/variance as part of compliance.
- Tools/workflows: Governance APIs; certified reward suites; audit trails and reporting.
- Assumptions/dependencies: Cross-model generalization; adversarial robustness against reward hacking; evolving legal standards.
- Personalized assistant generation with user-level constraints
- Sector: consumer AI, education
- Application: Natural-language constraints (via VLMs) to tailor generated content (style, accessibility, cultural norms); maintain diversity via SMC while enforcing personalized rules.
- Tools/workflows: Per-user reward profiles; flow-map enabled on-device or edge inference; transparency UI.
- Assumptions/dependencies: Efficient, privacy-preserving reward models; user consent and control.
- Standardization of efficiency metrics and schedules
- Sector: academia, benchmarking bodies
- Application: Establish thermodynamic length as a benchmark metric for reward-guided generation; publish standard schedules and resampling protocols to balance diversity and alignment.
- Tools/workflows: Open benchmarks; reference implementations; reporting formats.
- Assumptions/dependencies: Community consensus; reproducibility across models and data.
- Enterprise creative pipelines with automated QA loops
- Sector: marketing, product design
- Application: End-to-end pipelines where FMTT generates candidate assets, VLM/judge rewards perform QA, and SMC resampling maintains diversity—automating iterative human-in-the-loop workflows.
- Tools/workflows: Orchestrators integrating FMTT, VLM judges, and asset repositories; feedback capture and retraining hooks.
- Assumptions/dependencies: Scalability, budget controls; continual monitoring for reward exploitation; data governance.
- Medical imaging augmentation with strict constraints
- Sector: healthcare
- Application: Generate synthetic images meeting anatomical/contrast constraints for training downstream models; tilt generation toward underrepresented conditions.
- Tools/workflows: Domain-specific reward functions (radiologist-informed, physics-based); audit mechanisms for clinical safety.
- Assumptions/dependencies: Regulatory approvals; robust validation against real patient distributions; ethical safeguards.
- Developer tooling for reward authoring and gradient extraction
- Sector: ML tooling
- Application: IDEs/libraries that expose flow-map look-ahead X_{t,1}, velocity v_{t,t}, score s_t; enable easy composition of differentiable rewards (including VLMs) with automatic gradient checks and schedule recommendations.
- Tools/workflows: FMTT library + reward templates; gradient health indicators; integration with major diffusion frameworks.
- Assumptions/dependencies: Ecosystem support across models; stable APIs for VLM gradients; community adoption.
Notes on assumptions and dependencies across applications
- Flow-map availability: Many production models are pure diffusions; distillation (e.g., Align Your Flow) is needed to obtain reliable X_{t,1}(·) look-ahead. Performance depends on flow-map fidelity.
- Reward differentiability: VLM rewards typically provide logits for yes/no questions, enabling gradients through images; some rewards may require surrogates or straight-through estimators.
- Compute and latency: Reward gradients at each step add overhead; FMTT achieves better compute‑performance tradeoffs than multi-best‑of‑N, but budgets must be managed (NFE tracking).
- Exact vs search: Exact sampling needs SMC and importance weighting; search (top‑n/beam) improves rewards but can reduce diversity; thermodynamic length helps balance schedules.
- Reward hacking: Maximizing rewards can exploit loopholes; mitigations include carefully crafted questions, multiple judges, image‑quality checks, and off‑distribution regularization.
- Domain validation: Specialized domains (medical, finance) require validated rewards, robust calibration, and compliance with regulatory/ethical standards.
Collections
Sign up for free to add this paper to one or more collections.