Tilt Matching for Scalable Sampling and Fine-Tuning (2512.21829v1)

Abstract: We propose a simple, scalable algorithm for using stochastic interpolants to sample from unnormalized densities and for fine-tuning generative models. The approach, Tilt Matching, arises from a dynamical equation relating the flow matching velocity to one targeting the same distribution tilted by a reward, implicitly solving a stochastic optimal control problem. The new velocity inherits the regularity of stochastic interpolant transports while also being the minimizer of an objective with strictly lower variance than flow matching itself. The update to the velocity field can be interpreted as the sum of all joint cumulants of the stochastic interpolant and copies of the reward, and to first order is their covariance. The algorithms do not require any access to gradients of the reward or backpropagating through trajectories of the flow or diffusion. We empirically verify that the approach is efficient and highly scalable, providing state-of-the-art results on sampling under Lennard-Jones potentials and is competitive on fine-tuning Stable Diffusion, without requiring reward multipliers. It can also be straightforwardly applied to tilting few-step flow map models.

• The paper introduces Tilt Matching, a framework that adapts continuous-time generative models via exponential tilting for scalable sampling and reward-driven fine-tuning.
• It employs stochastic interpolants and a conditional covariance ODE to develop explicit and implicit algorithms that achieve variance reduction without relying on reward gradients.
• Experimental results show improved reward alignment, enhanced sample diversity in fine-tuning image models, and state-of-the-art performance on Boltzmann sampling benchmarks.

Tilt Matching for Scalable Sampling and Fine-Tuning

Problem Formulation and Theoretical Framework

Tilt Matching (TM) addresses the adaptation of continuous-time generative models—specifically flow and diffusion-based models—under exponential tilting of their terminal distributions. TM is motivated by two core downstream problems: (1) scalable sampling from unnormalized densities (e.g., Boltzmann distributions in statistical mechanics) and (2) fine-tuning pre-trained generative models to maximize an arbitrary reward function. Formally, given access to a base sampler generating $\rho_1(x)$, TM constructs a sequence of dynamics with terminal marginal $\rho_{1,a}(x) \propto \rho_1(x) e^{a r(x)}$ for $a \in [0,1]$ and scalar reward $r(x)$. The method is regime-agnostic: $\rho_1$ may be empirical data or the learned law of a pre-trained generative model.

Central to their approach is the usage of stochastic interpolants $I_t = \alpha_t x_0 + \beta_t x_1$, with $x_0 \sim \rho_0$, $x_1 \sim \rho_1$, and coefficients $\alpha_t, \beta_t$. The evolution of the velocity field $b_{t,a}(x)$ with respect to the annealing parameter $a$ is governed by an exact conditional covariance ODE:

$$\frac{\partial b_{t,a}(x)}{\partial a} = \mathrm{Cov}_a \left(\dot{I}_t^a, r(x_1^a) \mid I_t^a = x\right)$$

where the transport remains imbued with geometric regularity, supporting direct regression-based estimation and efficient neural function approximation.

Figure 1: Schematic overview of Tilt Matching: reward tilting induces a closed-form evolution for the interpolant velocity field, parameterized by conditional covariances.

This formalism is intimately connected to Doob’s $h$-transform and stochastic optimal control (SOC), with the tilted dynamics’ probability flow ODE corresponding to the optimal drift for a path measure reweighted by the terminal reward. Importantly, unlike standard SOC or Schrödinger bridge methodologies, TM eliminates the need for reward gradients or adjoint simulations, relying solely on regression against scalar rewards.

Algorithms: Explicit and Implicit Tilt Matching

The authors develop two algorithmic frameworks:

• Explicit Tilt Matching (ETM): A forward Euler discretization of the covariance ODE; for small increment $h$, the update

$$b_{t,a+h}(x) = b_{t,a}(x) + h \cdot \mathrm{Cov}_a(\dot{I}_t^a, r(x_1^a)|I_t^a=x)$$

can be efficiently regressed via Monte Carlo mini-batches.

• Implicit Tilt Matching (ITM): An infinite-order, discretization-free estimator corresponding to the fixed point of an importance-weighted regression, with variance strictly lower than explicit or weighted estimators. ITM regresses $b_{t,a+h}(x)$ so that:

$$\mathbb{E}[e^{h r(x_1^a)} (\hat b_t(x) - \dot I_t^a) | I_t^a = x] = 0$$

This matches cumulants of all orders, offering direct convergence to the tilted velocity field even for larger $h$.

Variance reduction via control variates is established, giving rise to a family of objectives (parameterized by an adaptive control variate $c_t(x)$) that interpolate between standard weighted flow matching and ITM, further stabilizing optimization.

Connection to Stochastic Optimal Control

An essential theoretical contribution is the identification that minimizers of ITM coincide with the drift of the probability flow ODE for the Doob $h$-transformed SDE with the appropriately matched diffusion. In contrast to conventional SOC approaches, which entail simulation of stochastic trajectories, reward gradient propagation, or solution of Hamilton–Jacobi–Bellman PDEs, TM achieves the same effect by simple local regression.

This connection affirms the method's statistical optimality: TM exactly recovers the controlled dynamics for any reward or energy function, subject to representational capacity and regression fidelity.

Numerical Experiments

Fine-Tuning Stable Diffusion 1.5

TM is deployed for reward maximization fine-tuning of Stable Diffusion 1.5 using the ImageReward function. Notably, the method does not require scaling the reward or derivative information. Performance is evaluated against state-of-the-art baselines (Adjoint Matching, DRaFT, DPO, ReFL) on CLIPScore, HPSv2, and DreamSim in addition to the reward objective. The results show strong improvements in reward alignment ($+0.23$ over base), CLIPScore, and human aesthetic preference scores, even without reward amplification, while also yielding competitive sample diversity.

Figure 2: Paired image samples for multiple prompts: Base vs. Tilt Matching, illustrating significant visual improvement in prompt adherence and photorealism.

Figure 3: Uncurated paired samples, Base vs. Tilt Matching. Consistent qualitative improvements, even outside cherry-picked settings.

Boltzmann Sampling: Lennard-Jones Potentials

TM achieves state-of-the-art effective sample sizes (ESS) and Wasserstein metrics on the well-studied LJ-13 and LJ-55 benchmarks. Using temperature annealing from a high-$T$ prior, TM produces samples with distributional properties nearly indistinguishable from ground truth MD data.

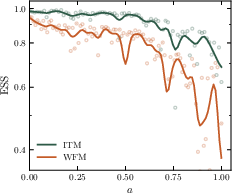
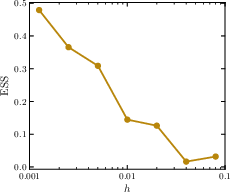
Figure 4: Comparison of TM samples to ground truth: interatomic distances and energy distributions match target closely.

Ensemble ESS and histogram-based Wasserstein-2 metrics confirm both the sampling efficiency and statistical accuracy benefits of TM, surpassing methods such as DDS, iDEM, and recent adjoint-based samplers.

Methodological Implications

TM generalizes and unifies reward-fine-tuning and distribution-matching flows, while circumventing key practical limitations of prior techniques. Key features include:

• No requirement for differentiable rewards (can optimize non-smooth human or black-box objectives).
• No need for backpropagation through simulation or differentiating trajectories, enhancing scalability to large models and long time horizons.
• Inherits regularity from base interpolant transportation, making neural regression robust and efficient.
• Variance reduction provably over weighted estimators, leading to improved sample efficiency and training stability.

The applicability extends across molecular and condensed matter simulation (Boltzmann sampling), generative image models, and settings where user feedback (as reward, preference, or other human-aligned signals) guides model update.

Limitations and Future Directions

While discretization-free ITM resolves several pathologies in flow-based model fine-tuning, cumulative regression error and representation bottlenecks may remain for high-dimensional or multi-modal rewards. The method’s efficacy with non-convex or adversarially misaligned rewards, and its sample efficiency for very large-scale generative models, warrant further investigation. Future advancement may explore:

• Online adaptation and meta-learning for reward-driven dynamics.
• Extensions to non-exponential family tilts or more general distribution-matching objects.
• Scalable implementations leveraging distributed, amortized estimators.
• Integration with RLHF/LLM reward modeling for large-scale text and multimodal generation.

Conclusion

Tilt Matching introduces a theoretically grounded, computationally efficient framework for generative model fine-tuning under reward tilts, rigorously bridging optimal transport, SOC, and practical deep learning regression. The approach supports rapid transfer from existing generative samplers to reward-aligned models for both scientific and creative tasks, with guarantees of variance efficiency and convergence. TM marks a significant contribution to the algorithmic toolbox for scalable, gradient-free optimization of dynamical generative models.